
2. ИМПУЛЬСНО - КОДОВАЯ МОДУЛЯЦИЯ (ИКМ)
2.1.Аналого-цифровой преобразователь (АЦП)
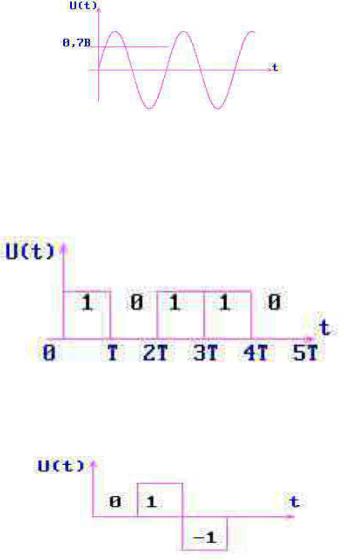
Непрерывные (аналоговые) сигналы могут принимать в любой момент времени сколь угодно близкие друг другу значения. Пример непрерывного сигнала - гармоническое колебание. На рисунке 2.1 отмечен уровень 0,7 вольт. Но данный сигнал принимает значения и 0,71 вольт, и 0,701 вольт, т.е. значения, сколь угодно близкие к 0.7 в.
Рис.2.1
Дискретные сигналы принимают в определенные (тактовые) моменты времени определенные значения, отличающиеся одно от другого на конкретную величину. Пример дискретного сигнала - двоичный (бинарный) сигнал. Он принимает только два значения 0 и 1 (рис.2.2.).
Рис.2.2.
В общем случае дискретный сигнал может принимать m значений (m-ичный сигнал). На следующем рис.2.3 приведена временная диаграмма троичного сигнала (он может принимать три значения: 0, +1, -1).
Рис.2.3.
Сигнал ИКМ - это двоичный сигнал, однозначно соответствующий исходному аналоговому сигналу. Устройство, преобразующее аналоговый сигнал в цифровой, называют аналого-цифровым преобразователем (АЦП).
Рассмотрим процесс формирования сигнала ИКМ по рис. 2.4.
6
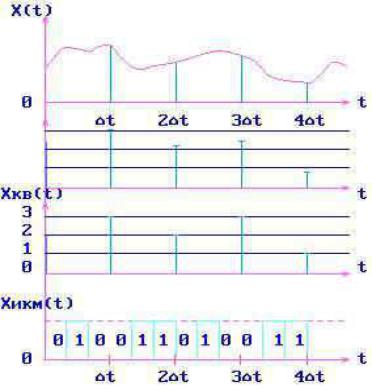
Переход от непрерывного сигнала к сигналу ИКМ включает три основные
операции:
1)Дискретизация исходного непрерывного сигнала х(t), показанного на рис.2.4.а в соответствии с теоремой Котельникова; интервал дискретизации равен:
Т = |
π |
= |
1 |
, |
(2.1) |
|
ω |
|
|
||||
|
в |
|
2F |
|
||
|
|
|
в |
|
||
если ωв=2πFв - ширина спектра исходного сигнала. В результате дискретизации получим сигнал хд(t), показанный на рис.2.4.б.
2) Квантование по уровню импульсов-отсчетов. Диапазон допустимых значений x(t) разбивается на разрешенные уровни – уровни квантования. Операция квантования состоит в том, что вместо истинного значения амплитуды импульса передается ближайший разрешенный уровень. Пусть уровни квантования 0,1,2,3 и т.д. вольт. Тогда вместо 0,2 вольт передаем 0; вместо 1,4 вольт - 1 вольт и т.д. В результате квантования получим сигнал хкв(t), показанный на рис.2.4.в.
а)
Хд(t)
б)
в)
г)
Рис.2.4.
3) Кодирование квантованных импульсов - отсчетов. Кодирование состоит в том, что вместо квантованного уровня передается комбинация кодовых символов. Если код – двоичный, то символами кода являются 1 и 0. Количество различных символов, которые образуют кодовые комбинации, называется основанием кода m. Количество символов в кодовой комбинации называется длиной кодовой комбинации n. Общее количество кодовых комбинаций равно N=mn .
7
Примитивное кодирование состоит в том, что номер уровня квантования записывается двоичным числом, т.е. в виде двоичной кодовой комбинации (m=2). Предположим, что комбинация состоит из трех импульсов n=3. Тогда десятичным номерам уровней соответствуют следующие двоичные числа:
0=000, 1 = 001; 2 = 010; 3 = 011; 4 = 100; 5=101; 6=110; 7=111.
В результате кодирования мы получили двоичный сигнал ИКМ хИКМ(t) на рис.2.4.г, однозначно соответствующий исходному непрерывному сигналу х(t) с заданной точностью.
Сигнал ИКМ передается в линию связи и поступает на вход приемника. Для восстановления на приемной стороне исходного непрерывного сигнала выполняются следующие операции:
1.Декодирование принятых кодовых комбинаций; т.е. принятая двоичная комбинация превращается в соответствующее десятичное число: 000 превращается в 0 вольт, 001 в 1 вольт, 010 в 2 вольта, 011 в 3 вольта …. и т.д. 111 в 7 вольт.
2.Полученные импульсы – отсчеты подаются на вход восстанавливающего фильтра, который теоретически должен быть идеальным фильтром нижних частот (ИФНЧ).
На выходе этого ИФНЧ получим с заданной точностью исходный непрерывный сигнал x(t)€ . Среднеквадратическая погрешность восстановленного сигнала x(t)€ относительно x(t) должна быть не более заданной величины. Устройство, преобразующее цифровой сигнал в аналоговый, называют цифро-аналоговым
преобразователем (ЦАП).
Достоинства ИКМ.
1.Сигнал ИКМ – цифровой сигнал и поэтому использование ИКМ позволяет реализовать преимущества цифровой аппаратуры по сравнению с аналоговой: большая степень интеграции, унификации и стандартизации; меньше объем аппаратуры; больше точность и стабильность параметров.
2.Сигнал ИКМ имеет более высокую помехоустойчивость благодаря тому, что его можно регенерировать. Регенерация – это восстановление частично пораженных помехой импульсов сигнала.
z(t) |
1 |
0 |
1 |
0 |
1 |
а)
v
 t
t
б) uр(t)
t
Рис. 2.5.
8
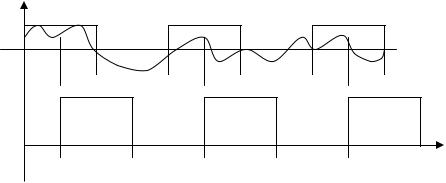
На рис.2.5 показан сплошной линией процесс z(t) - сигнал в сумме с шумом на входе регенератора. Тонкой линией показан передаваемый двоичный сигнал 1 и 0.
Регенератор в тактовые моменты времени, в середине посылки, сравнивает принятый процесс с пороговым напряжением v. Если напряжение u(t) > v, то на выходе регенератора появляется 1, а если u(t) < v , то 0. Из рис.2.5.б видно, что сигнал на выходе регенератора совпадает с переданным – сигнал регенерирован, восстановлен в первозданном виде.
Недостатки ИКМ.
1. Ширина спектра ПИКМ сигнала ИКМ значительно больше ширины спектра
исходного аналогового сигнала. Определим ширину спектра сигнала ИКМ, если ширина спектра аналогового сигнала равна FВ. За время ∆t =1/2FВ необходимо передать комбинацию сигнала ИКМ из n импульсов. Если число уровней квантования N, то:
n=log2N
Следовательно, длительность одного импульса равна Т=1/2nFВ . Ширина спектра прямоугольного импульса, т.е. ширина спектра ИКМ, обратно пропорциональна длительности импульса Т:
ПИКМ=1/T=2nFВ (2.2)
Обычно используются сигналы ИКМ с длиной комбинации 6 – 9. Следовательно, ширина спектра ИКМ в 12-18 раз больше ширины спектра исходного непрерывного сигнала.
2. Квантование импульсов - отсчетов по уровню эквивалентно наложению на сигнал ИКМ помехи, которая называется «шум квантования».
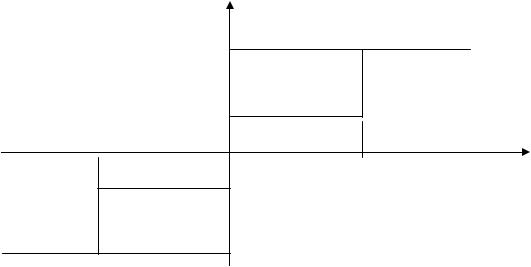
На рис.2.6 нарисована характеристика квантователя, т.е. зависимость уровней квантования yк от порогов квантования хк. Из рис.2.6. видно, что данный квантователь имеет 4 уровня квантования: у0, у1 , у2 , у3 и 3 порога х0 , х1 , х2 . Если значения входного сигнала х лежат в пределах от - ∞ до х0 , то на выходе квантователя имеем уровень у0 .
yк
y3
y2
х0 х1
х2 хк
y1
y0 |
Рис.2.6. |
9

Если значения входного сигнала х лежат в пределах от х0 до х1 , то на выходе квантователя имеем уровень у1 . Если значения входного сигнала х лежат в пределах от х1 до х2, то на выходе квантователя имеем уровень у2 . Если значения входного сигнала х лежат в пределах от х2 до ∞, то на выходе квантователя имеем уровень у3.
Рассчитаем дисперсию шума квантования σ2, т.е. среднюю мощность шума квантования на единичном сопротивлении. Пусть ∆ = (yк - yк-1) - шаг квантования, т.е. расстояние между соседними уровнями квантования.
Мгновенные значения шума квантования равномерно распределены на интервале от -∆/2 до ∆/2, т.е. функция плотности вероятности шума квантования равна:
W(x)=1/∆ при |х| ≤ 0.5 ∆.
Следовательно, дисперсия шума квантования равна:
/ 2 |
/ 2 |
x |
2 |
|
2 |
σ 2 = ∫ x 2 W (x) dx = ∫ |
|
dx = |
= |
||
|
|
||||
− / 2 |
− / 2 |
|
|
|
12 |
|
|
|
(2.3) |
||
|
|
|
|
|
|
U2
=max ;
−1)212(N
∆=Umax/(N -1) ;
N – количество уровней квантования.
Umax- максимальный уровень однополярного сигнала.
Для качественной передачи сигнала методом ИКМ необходимо обеспечить отношение мощности сигнала к дисперсии шума квантования, порядка, 30дБ. Это условие удовлетворяется для больших уровней квантования, но не удовлетворяется для малых уровней. Если увеличить число уровней квантования N, то дисперсия шума квантования уменьшится, но при этом пропорционально logN увеличится ширина спектра сигнала ИКМ. Проблема решается путем применения неравномерного квантования: малые уровни квантуются с малым шагом квантования, а большие уровни квантуются с большим шагом квантования. Технически это удобно реализовать путем использования нелинейных устройств: компрессора на передаче и экспандера на приеме. Характеристика компрессора соответствует «µ- закону» или «А-закону». В России рекомендован «µ- закон» при
µ=255: |
|
uвых=lg(1+ µ uвх)/lg(1+ µ) |
(2.4) |
uвых |
|
1 |
|
Рис.2.7
0 |
1 |
uвх |
10
На рис.2.7 показаны характеристики компрессора (сплошная линия) и |
|||||||||||||||||
экспандера (пунктирная линия). На передаче дискретные импульсы-отсчеты |
|||||||||||||||||
проходят через компрессор, у которого коэффициент передачи |
для |
малых |
|||||||||||||||
амплитуд больше, чем для |
больших. Далее стоит квантователь с постоянным |
||||||||||||||||
шагом квантования. В результате получаем неравномерное квантование: |
|||||||||||||||||
маленькие уровни квантуются с маленьким шагом, |
а большие – |
с большим. |
|||||||||||||||
Экспандер на приеме компенсирует нелинейные искажения, вносимые |
|||||||||||||||||
компрессором. Устройство, состоящее из компрессора и экспандера, |
называют |
||||||||||||||||
компандером. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим оптимизационную задачу. Пусть шум квантования определяется |
|||||||||||||||||
(2.3), а энергетический спектр сигнала при заданной мощности имеет вид: |
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
exp(− f |
2 |
∞ |
|
|
∞ |
|
|
Пх ); |
|
|
|
|
|
G( f ) = |
α |
|
2 ); |
∫G( f )df |
= σ 2 ; |
ε 2 |
= ∫G( f )df |
= 1 − Ф( |
|||||
|
|
|
|
|
|
2π |
2α |
|
0 |
|
|
Пх |
|
|
α 2 |
||
Тогда значения сигнала с вероятностью 0.997 заключены в пределах ±3σ и шаг |
|||||||||||||||||
квантования равен 6σ/(N-1). Тогда суммарная дисперсия шума квантования и скп |
|||||||||||||||||
фильтрации может быть записана в виде : |
|
|
|
|
|
|
|||||||||||
2 |
2 |
|
2 |
36σ 2 |
|
|
Пх |
|
3σ 2 |
Пикм |
|
|
|
|
|||
σ Σ |
= σ кв + |
ε |
|
= 12(2n |
− 1)2 + [1 − Ф(α 2 )] = |
|
(2n |
− 1) 2 + [1 − Ф( 2nα |
2 )]; |
|
|
|
|||||
Пусть заданы Пикм и дисперсия сигнала σ2. Тогда вариационная задача состоит в |
|||||||||||||||||
поиске оптимального значения n при условии: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫G( f )df = σ 2 |
|
= const; |
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
3.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
3 |
|
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.5. |
||
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|

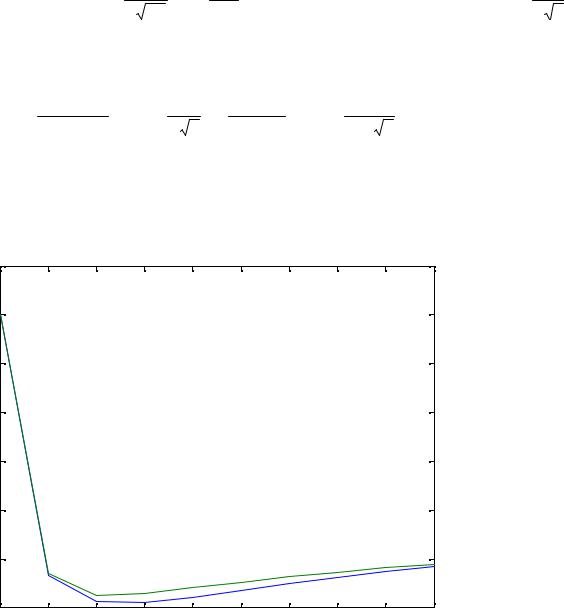
Численное решение при Пикм=64000 Гц , σ2=1вт и α=4000 Гц показано на рис.2.5 (кривые соответствует различным энергетическим спектрам сигнала вида). Оптимальные значения n равны 4 и 3.
2.2. Помехоустойчивость регенерации сигнала ИКМ методом однократного отсчета
Регенерация сигнала ИКМ осуществляется регенератором (рис.2.6), на вход которого поступает процесс z(t), представляющий собой сумму сигнала и шума.
|
z(t) |
|
|
|
[zn] |
|
ПФ |
Усилитель |
|
Отсчетное |
Пороговое |
||
|
|
|
||||
|
|
|
|
устройство |
|
устройство |
|
|
|
|
|
|
|
Источник
порогового Рис.2.6. напряжения
Всостав регенератора входят:
-полосовой фильтр, выделяющий информационный сигнал, пораженный помехами;
-усилитель;
-отсчетное устройство, которое берет отсчеты процесса z(t) в тактовые моменты времени (T/2 + kT) ;
-пороговое устройство, в котором отсчеты z(T/2 + kT) сравниваются с пороговым напряжением V, поступающим от источника порогового напряжения;
если z(T/2 + kT) > V, то на выходе порогового устройства 1, если z(T/2 + kT)<V, то на выходе порогового устройства 0.
Т.о. на выходе отсчетного устройства получим одномерный вектор-строку [zn], координаты которого равны отсчетам процесса z в тактовые моменты времени: [zn]=[z(T/2), z(T/2+T)…..z(T/2+nT)].
На выходе порогового устройства получим вектор-строку, который пусть имеет вид [un ] = [1,0,0,1,.....1] . Этот вектор называется оценкой информационного сигнала
и координаты его, в отсутствии помех, должны быть равны переданному сигналу. Очевидно, что под действием помех некоторые импульсы искажаются и будут приняты неверно. Если приняли '0' , а была передана '1', то эта ошибка
называется 'пропуск сигнала'. Вероятность принятия 0 при передаче 1 обозначим p(0/1). Если приняли '1' , а был передан '0', то эта ошибка называется 'ложная тревога'. Вероятность принятия 1 при передаче 0 обозначим p(1/0).
Рассчитаем зависимость р(1/0) и р(0/1) от порогового напряжения V, если шум x(t), поражающий сигнал – нормальный. Вероятность p(1/0) равна вероятности p(z(t)>V) и равна вероятности p(x(t)>V), т.к. при передаче 0 процесс z(t)=x(t). Так как ФПВ помехи x(t) – гауссова с дисперсией σ2 , т.е.:
12
|
|
|
|
|
|
|
W (x) = |
|
1 |
е− |
х2 |
|
|
|
|
||
|
|
|
|
|
|
|
σ |
2σ 2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
то искомая вероятность равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
∞ |
1 |
е |
− x22 |
dx |
= |
1 |
∞ |
− у2 |
|
V |
|
|
p(1/ 0) = p(x > V ) = ∫ |
2π |
2σ |
2π |
∫ е 2 dy = |
1 − F |
; |
|
||||||||||
|
|
|
|
|
V σ |
|
|
|
|
V / σ |
|
|
σ |
(2.5) |
|||
|
|
V |
|
1 |
V / σ |
− у2 |
|
|
|
|
|
|
|
|
|
|
|
где |
|
− интеграл |
Лапласа. |
|
|
|
|
||||||||||
F |
= |
2π |
∫ е |
2 dy |
|
|
|
|
|||||||||
|
|
σ |
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, вероятность р(0/1)=р(z(t)<V)=p(Uc+х(t)<V)=p(x(t)<V-Uc) может |
|||||||||||||||||
быть записана в виде: |
|
|
|
|
|
|
|
|
V −Uс |
|
|
|
|
|
|
||
|
|
|
|
V −Uс |
|
|
|
|
|
|
|
|
V − U |
|
|
||
p(0 /1) = p(x < V − U с ) = |
1 |
− x22 |
dx = |
1 |
σ |
− у2 |
|
|
|||||||||
∫ |
2π |
е 2σ |
2π |
∫ |
е |
2 dy = F |
σ |
с ; |
(2.6) |
||||||||
|
|
|
|
−∞ σ |
|
|
|
|
−∞ |
|
|
|
|
|
|||
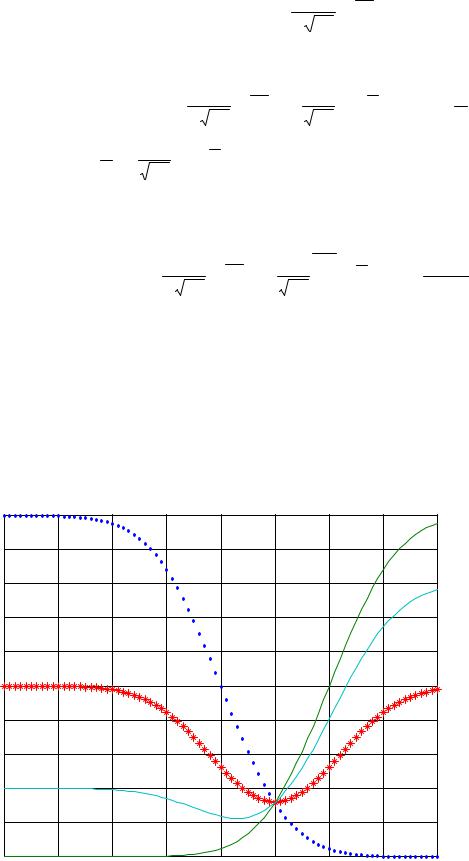
Зависимость р(1/0) и р(0/1) от порогового напряжения V показана на рис. |
|||||||||||||||||
2.9 (кривые 1 и 2, соответственно) |
для |
произвольно выбранного |
отношения |
||||||||||||||
Uc/σ=2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полной характеристикой помехоустойчивости является средняя |
|||||||||||||||||
вероятность ошибки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p= |
p(1)p(0/1)+p(0)p(1/0); |
|
|
|
|
|
|
|
|
|
|
(2.7) |
|||||
p(1), p(0) - априорные вероятности передачи 1 или 0. |
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | |
|
|
|
|
|
|
|
|
|
|
||
-4 |
-3 |
-2 |
-1 |
|
|
1 |
|
2 |
|
3 |
|
4 |
|
|
|||
|
|
|
|
|
|
V1о п т V 2о п т |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Рис.2.7. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
На рис.2.7 даны зависимости средней вероятности ошибки для р(1)=р(0)=0.5 (кривая 3); и для р(1)=0.2, р(0)=0.8 (кривая 4).
Пороговое напряжение, при котором средняя вероятность ошибки минимальна, называется оптимальным пороговым напряжением Vопт .
Оптимальное значение порогового напряжения может быть найдено как решение уравнения:
dр |
= |
d |
[р(0) |
|
+ р(1) р(0 /1)] = |
d |
р(0)[1 − F ( |
V |
)] + р(1) F ( |
V − U |
с |
|
=0; (2.8) |
|
|
|
р(1/ 0) |
|
|
|
|
) |
|||||||
|
|
|
σ |
σ |
|
|||||||||
dV |
|
dV |
|
|
|
dV |
|
|
|
|
|
|||
Решение этого уравнения для нормальной помехи дает следующее выражение для оптимального порогового напряжения:
V = |
U с |
− σ 2 |
ln |
р(1) |
; |
(2.9) |
|
|
|||||
опт |
2 U с |
|
р(0) |
|
||
|
|
|
||||
На рисунке отмечены оптимальные пороговые напряжения V1опт и V2опт для двух кривых, соответствующих разным значениям априорных вероятностей.
14

2. ОПТИМАЛЬНЫЙ ПРИЕМНИК. ПОТЕНЦИАЛЬНАЯ ПОМЕХОУСТОЙЧИВОСТЬ
2.1 Алгоритм оптимального приема.
На вход приемника поступает процесс z(t), равный сумме одного из возможных вариантов сигнала ui(t) и помехи x(t):
z(t)= ui(t) + x(t); |
(2.1) |
Способность системы связи препятствовать мешающему влиянию помех
называется помехоустойчивостью системы связи. |
Максимальная достижимая |
||
помехоустойчивость называется потенциальной помехоустойчивостью. |
|||
Количественной мерой помехоустойчивости является вероятность ошибки р: |
|||
р = lim |
N ош |
; |
(2.2) |
|
|||
N → ∞ |
N |
|
|
N - общее количество переданных символов, посылок, сообщений;
Nош - количество ошибок, т.е. количество неверно принятых символов, сообщений.
Если N достаточно велико, но не бесконечно, то р = Nош/N называют частостью ошибок.
Высокой помехоустойчивости соответствует малая вероятность ошибки. Низкой (плохой) помехоустойчивости соответствует большая вероятность ошибки.
Потенциальной помехоустойчивости соответствует минимальная
вероятность ошибки.
Реальные системы связи работают с такими вероятностями ошибок: р=10-1 – 10 -3 - удовлетворительное качество; р=10-4 – 10 -6 - хорошее качество; р=10-7 – 10 -9 - отличное качество.
Т.к. на полезный сигнал в линии связи накладываются помехи, то задача разработчика - сконструировать приемник, который наилучшим образом выделяет сигнал из помех.
Приемник, реализующий потенциальную помехоустойчивость, называется оптимальным или идеальным приемником.
Оптимальный приемник (ОП) дает минимальную вероятность ошибки.
Она может быть и очень большая, но никакой другой приемник не даст меньшую вероятность ошибки.
Правило работы оптимального приемника может быть только статистическим. Поясним этот вывод. На рисунке 2.1 показан процесс z(t) на входе приемника, т.е. сигнал плюс шум:
Не удаетсяотобразить связанный рисунок. Возможно, этот файл был перемещен, переименован или удален. Убедитесь,что ссылкауказывает на правильный файл и верное размещение.
Рис.2.1.
88
