Лабораторные работы / Методички / лаба №20

План УМД на 2015/2016 уч .г .

ЛАБОРАТОРНАЯ РАБОТА № 20 – ПК

ЭФФЕКТИВНОЕ И ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ

Составитель: Сухоруков А.С. , доцент

Издание утверждено советом ОТФ-2. Протокол №1 от 31.08.2015 г. Рецензент: Парамонов Ю.В. , доцент

2

А. ЭФФЕКТИВНОЕ КОДИРОВАНИЕ

1.А. ЦЕЛЬ РАБОТЫ

Изучить основные способы увеличения энтропии дискретного источника и принципы эффективного кодирования.

2.А. ДОМАШНЕЕ ЗАДАНИЕ

1. Задан дискретный источник двоичных сообщений, который производит слова, состоящие из двух букв А и М. Всего возможно четыре различных сообщения, слова : АА. AM, МА, ММ. Рассчитайте вероятность каждого слова р(АА), р(АМ), р(МА), р(ММ), если заданы (см. таблицу А) безусловные вероятности р(А), р(М) и условные вероятности.

(р(А/М) - вероятность буквы A, если первой в слове была буква М; остальные обозначения аналогичны).

2.Рассчитайте энтропию источника Н и его избыточность R.

3.Закодируйте слова четверичным кодом и рассчитайте его энтропию и избыточность.

4.Закодируйте четыре слова безызбыточным кодом с префиксными свойствами, построив кодовое дерево. Рассчитайте энтропию нового двоичного кода, его избыточность и среднюю длину кодовой комбинации.

5.Запишите выражения, соответствующие передаче нуля и единицы с помощью двоичной фазовой модуляции. Запишите выражения, соответствующие передаче различных комбинаций из двух символов, «дибитов», с помощью четырехпозиционной ФМ. Нарисуйте временные диаграммы сигналов двоичной и четырехпозиционной ФМ.

Определите максимальное значение энтропии для m=2 и m=4.

Таблица А.

3

Б. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ

1.Б. ЦЕЛЬ РАБОТЫ

Изучите принципы помехоустойчивого кодирования, освоить алгоритм кодирования и алгоритм декодирования для блочного двоичного систематического кода.

2.Б. ДОМАШНЕЕ ЗАДАНИЕ

1. Задана строка порождающей матрицы кода (7,3) в таблице Б. Составить порождающую матрицу заданного кода G.

2.Сформировать разрешенные кодовые комбинации кода (7,3), определить минимальное кодовое расстояние и исправляющую способность полученного кода.

3.Составить проверочную матрицу данного кода Н.

4.Вычислить синдромы и вектора ошибок, соответствующие одиночной ошибке для каждого из 7 символов принятой кодовой комбинации.

5.Составить структурную схему кодека.

Таблица Б.

3. ОПИСАНИЕ ПРОГРАММЫ

Программа LR-20 состоит из двух частей: первая часть - информационная вторая часть – контролирующая. Информационная часть программы содержит основные сведения о способах увеличения энтропии, способах эффективного

4

кодирования и формулы для расчета параметров эффективного кода (раздел А) и, соответственно, основные сведенияо помехоустойчивых кодах, алгоритмах кодирования и декодирования для блочного двоичного кода (7,3) (раздел Б).

Контролирующая часть программы автоматически оценивает качество усвоения студентом теоретического материала. Эта часть работы выполняется в диалоговом режиме. По запросу компьютера студент должен вводить предварительно рассчитанные параметры. После этого компьютер оценивает правильность ответа и подсчитывает общее число ошибок.

4.ЛАБОРАТОРНОЕ ЗАДАНИЕ

1.Проработать информационную часть программы: изучить основные положения теории эффективного кодирования, записать основные формулы, усвоить принципы построения кодового дерева (раздел А), изучить основные принципы помехоустойчивого кодирования, алгоритмы кодировании и декодирования для кода (7,3) (раздел Б).

2.Выполнить контролирующую часть программы: записать исходные вероятности, задаваемые компьютером ( возврат к ним в дальнейшем невозможен), либо порождающую матрицу; рассчитывать и вводить по запросу компьютера числовые значения величин (с точностью двазнака после запятой) и кодовые комбинации.

3. После окончания лабораторной работы компьютер выдаст сообщение об общем количестве допущенных ошибок и предлагает студенту пригласить преподавателя

5. СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать исходные данные для расчета, результата вычислений основных параметров, кодовое дерево, временные диаграммы, таблицу разрешенных кодовых комбинаций, синдромы и вектора ошибок.

6.ВОПРОСЫ ДНЯ ПОДГОТОВКИ К РАБОТЕ

1.Что такое энтропия? Как рассчитать энтропию дискретного источника независимых сообщений?

2.Как рассчитать энтропию дискретного источника зависимых сообщений?

3.Назовите способы увеличения энтропии.

5

4.Каков алгоритм построения кодового дерева?

5.Нарисуйте временные диаграммы сигналов двух- и четырехпозиционной ФМ.

6.Как рассчитать среднюю длину кодовой комбинации?

7.Что такое кодовое расстояние и минимальное кодовое расстояние для кода?

8.Каков алгоритм кодирования для кода (7.3)?

9.Каков алгоритм декодирования для кода (7.3)?

ПРИЛОЖЕНИЕ А.

Эффективное кодирование - это такое кодирование, которое позволяет увеличить энтропию Н дискретного источника информации, т.е. среднее количество информации, приходящееся на один символ, сообщение, слово. Энтропия измеряется в двоичных единицах (битах) на символ, например, энтропия H = 1.5 бит/символ. Чем больше энтропия источника сообщений, тем больше количество информации, переносимое одним символом. Следовательно, при той же скорости поступления символов в канал будет больше скорость передачи информации, т е. количество информации, передаваемой в единицу времени.

На величину энтропии влияют три основных фактора: корреляционные связи между сообщениями; вероятность каждого из сообщений; основание кода.

Так как наличие корреляционных связей и неравновероятность сообщений уменьшают энтропию, то можно указать три основных способа увеличения энтропии:

1)укрупнение алфавита (декорреляция сообщений),

2)построение кода, символы которого равновероятны,

3)увеличение основания кода.

Пусть задан двоичный источник дискретных сообщений, который производит слова, состоящие из двух букв Аи М. Количество возможных слов - четыре: AM, МА, АА, ММ. Между буквами в словах существуют статистические святи. Между отдельными словами статистических связей нет. Отдельные слова, в общем случае, неравновероятны. Рассчитаем энтропию H такого источника и найдем способы ее увеличения. Пусть вероятностные характеристики источника следующие:

6

Так как слова независимы, то энтропию источника можно посчитать как энтропию источника независимых слов. Но, для определения энтропии на букву источника, полученный результат следует разделить на количество букв в слове, то есть на 2:

Где p(Si) – вероятность i-гo слова;

m - общее количество слов (в данном случае m= 4),

n -количество букв в слове (в данном случае n = 2);

lg - десятичный логарифм.

Избыточность источника R равна:

где = log(m) = 1 дв. ед./символ. (m – основание кода исходного источника, равное 2).

1. Укрупнение алфавита источника сообщений.

Для увеличения энтропии будем кодировать не отдельные буквы, а целые слова

S1 = AM закодируем символом 0, S2 = МЛ закодируем символом 1,

S3 = ММ закодируем символом 2, S4 = AA закодируем символом 3.

7

(Корреляционные связи между словами гораздо меньше, чем между буквами).

При этом увеличивается основание кода m= 4 (усложняется кодек) и снижается помехоустойчивость.

Энтропия: Где p(Si) – вероятность i-гo слова;

m -общее количество слов, основание нового кода (в нашем примере 4); Ig –десятичный логарифм.

p(S1) = p(AM); p(S2) = p(MA); p(S3) = p(MM); p(S4) = р(AА). В результате расчета получим: Н=1.656 дв.ед./символ. Избыточность нового кода:

где = log m = 2 дв. ед./символ ( m - основание нового кода, равное 4).

2.Второй способ увеличения энтропии состоит в том, что неравновероятные сообщения кодируются новым кодом, символы которого должны быть равновероятны.

Это достигается, например, кодированием в соответствии с алгоритмом Хаффмена.

Этот алгоритм состоит из следующих операций:

а) Расположить исходные сообщения в порядке убывания вероятностей;

б) Объединить два наименее вероятных сообщения в одно, вероятность которого равна сумме вероятностей объединяемых сообщений (точка объединения сообщений называется «узлом кодового дерева»);

в) Повторять шаги а) и б) до тех пор, пока не получим одно сообщение с вероятностью 1. Эта точка называется «вершиной кодового дерева».

Например, кодовое дерево имеет такой вид в нашем случае:

8

Чтобы закодировать исходные сообщения новым кодом, надо идти от вершины дерева к сообщениям. Если в узлах кодового дерева вы идете вверх, то в кодовую комбинацию пишется 1, а если вниз, то 0. Для нашего примера получим такие кодовые комбинации:

S4 – 1, S2–00, S1–011, S3 –010.

Проследите кодирование по кодовому дереву.

Энтропия нового двоичного кода рассчитывается следующим образом. Пусть слова исходного источника S1, S2, S3. S4 имеют вероятности и закодированы как в нашем примере. Из 100 среднестатистических сообщений будем иметь S1 - 14 сообщений; S2 - 21сообщение; S3 - 9 сообщений; S4 - 56 сообщений. В соответствии с новым кодом имеем:

•14 сообщений S1, т.е. 14 символов 0 и 28 символов 1;

•21 сообщение S2,т.е. 42 символа 0;

•9 сообщений S3, т.е. 9 символов 1 и 18 символов 0; •56 сообщений S4, т.е. 56 символов 1.

Таким образом, 100 среднестатистических сообщений содержат: символ 0: N0=14*1 + 21*2 + 9*2 = 74 штуки;

символ 1: N1 = 14*7 +9*1 * 56*1= 93 штуки;

Т.о. вероятность появления 0 равна: P0 = N0/ (N0+ N1) = 0.443;

9

вероятность появления 1 равна P1=1- 0.443 = 0.557. Энтропия нового двоичного кода равна:

дв.ед./символ.

= log 2 = 1 бит/символ.

Избыточность. . Средняя длина кодовой комбинации:

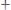
символ/сообщение, где n1,n2, n3, n4 – длина кодовой комбинации для S1, S2, S3, S4.

3. Третий способ увеличения энтропии - увеличение основания кода m.

Будем считать, что символы нового двоичного кода (m= 2), полученного в п.2, практически равновероятны. Комбинации из двух двоичных символов (бит) называют дибитами. Дибиты этого кода 00, 01, 10, 11 будем кодировать четверичным кодом:

00 - закодируем символом 0; 01 - закодируем символом 1;

10 - закодируем символом 2; 11 - закодируем символом 3.

Каждый символ нового четверичного кода несёт уже не 1 двоичную единицу информации (бит), а 2, т.к. при m=4 = log4 = 2 [бит/символ].

Два символа двоичного кода длительностью 2Т несут, максимум, 2 бита информации (m=2; 1бит/символ;n = 2;l = n * = 2бита). Один символ четверичного кода длительностью Т несет тоже 2 бита информации (m = 4; = бит/символ;n = 1; l =n;= 2 бита). Следовательно, мы в 2 раза увеличили скорость передачи информации. При этом помехоустойчивость приёма уменьшается.

Пусть двоичные символы передаются с помощью ДФМ; т.е. символы 0 и 1 передаются колебаниями с фазами k* 180, k = 0 или 1:

; .

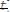
Пусть дибиты 00, 01, 10,11 кодируются четырехпозиционной ФМ с фазами k*90° (k - десятичное число, соответствующее двоичному числу дибита);

.

10