3 сем Крупин / отчет лаба 4 v5

Лабораторная работа №3

По математическим методам моделирования физических процессов

Горьков И.А.

ТФ-10-20

Крупин Г.В.

Вариант №19

1. Заполним последние два столбца таблицы.

N	Страна	1950	1960	1970	1980	1990	2000	2010	2020
4.1.0	Весь мир	2507	3050	3700	4400	5235	6082	6922	7753
4.1.12	Чили	6	7.5	9.5	11	13	16

Так как данные в таблице не совпадают с реальными, что приводит к сильной погрешности, заменим их.

4.1.12

Чили

6.6

8.1

9.8

11.4

13.3

15.3

17.1

19.1

Зададим исходные данные: векторы x и y, число точек (n+1), степени многочленов (m).

Напишем подпрограмму, вычисляющую вектор а коэффициентов а₀, …, а_m многочлена степени m по методу наименьших квадратов.

Полином степени m в точке t вычисляем следующим образом:

Среднеквадратичное отклонение полинома степени m определяем следующим образом:

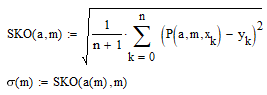
Определим среднеквадратичное отклонение многочленов степени m = 0...7.

Как видно из вектора, наилучшим приближением обладает многочлен степени 6. С помощью него определим значение численности населения в 2019 году.

Сравним полученное значение с актуальным, которое равно 18.952.

Построим график полинома 6 степени (с точками исходных данных).

Вывод: Население в Чили получилось равным 18.898, что близко к значению, взятому из интернета – 18.952.

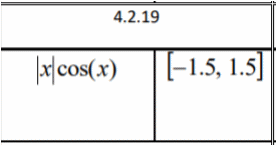
Задача 4.2. Функция f(x) является кусочно-гладкой функцией. Приблизить функцию многочленами Лагранжа 2, 6,10 степеней. Для каждого случая построить график погрешности. Предложить и реализовать способ интерполяции, при котором величина погрешности не будет превышать величины

Погрешность:

Погрешность:

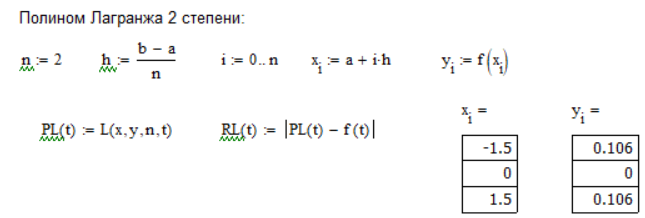
Погрешность:

Реализация квадратичного сплайна:

И збавимся от излома разделив отрезок на 2 отрезка [-1.5;0] и [0;1.5]

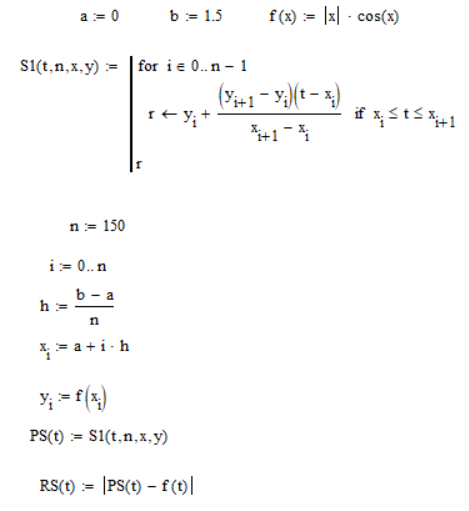
Для второго отрезка

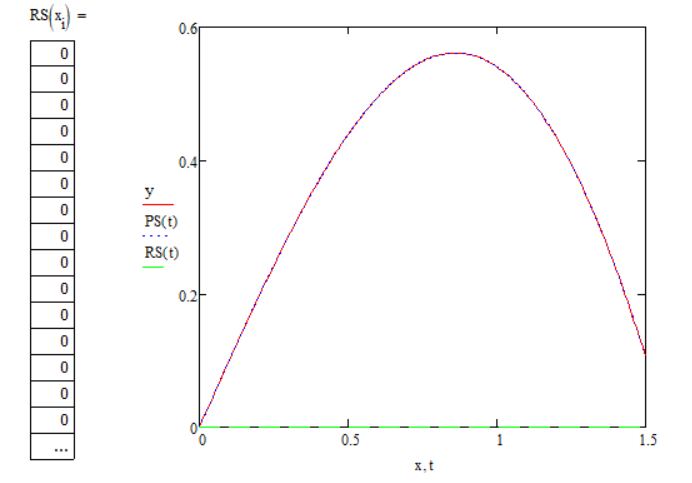
Вывод: точность достигнута

Задача 4.3 Постановка задачи: зависимость между величинами x и y описывается функцией y=f(x, a, b), где a и b – неизвестные параметры. Найти эти параметры, сведя исходную задачу к линейной задаче метода наименьших квадратов.

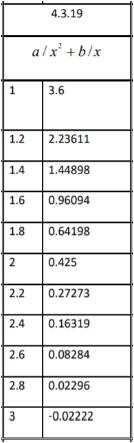
Сведем исходную задачу к линейной задаче метода наименьших квадратов, для этого произведем замену:

Тогда уравнение будет иметь вид: .

Теперь решаем линейную задачу метода наименьших квадратов.

Выражение должно стремиться к минимуму. Взяв производные по a и b, придем к системе:

Решив данную систему, получим корни уравнения: a= 5.5; b= -1.9.

Отсюда следует:

Листинг программы:

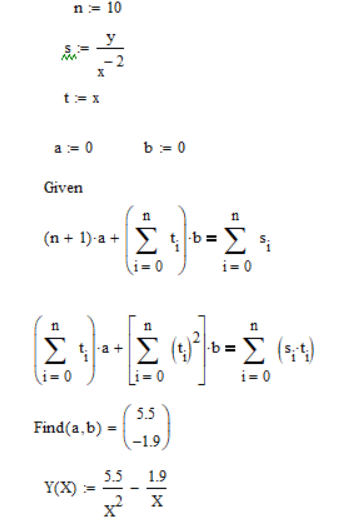
Сравним полученную функцию с исходными данными.