
3 сем Крупин / отчет лаба 1
.docxЗадача 1.1.
Постановка
задачи: Найти
сумму ряда S= .
Вычислить значения частичных сумм ряда
.
Вычислить значения частичных сумм ряда
 и найти величины абсолютной и относительной
погрешностей при значениях
и найти величины абсолютной и относительной
погрешностей при значениях
 =
=
 ,
,

 ,
,
 .
.
Решение
задачи. Используя
средства пакета МC,
получим значение S=19.
Введем функцию
 .
Тогда абсолютную погрешность можно
определить с помощью функции
.
Тогда абсолютную погрешность можно
определить с помощью функции
 ,
а относительную погрешность определяется
как
,
а относительную погрешность определяется
как
 .
.
Результаты вычислительного эксперимента оформим в виде таблицы.
|
S(N) |
|
Количество верных цифр результата |
|
Ответ |
10 |
10.21428571 |
8.78571429 |
1 |
46% |
S=10±9 |
|
17.37100737 |
1.62899263 |
1 |
8.6% |
S=17.4±1.6 |
|
18.98201888 |
0.01798112 |
3 |
0.0946% |
S=18.98±0.02 |
|
18.9999982 |
0.0000018 |
7 |
0.0000094% |
S=18.999998±0.000002 |
Листинг программы
Задача 1.2
Постановка задачи: найти значения машинного нуля, машинной бесконечности, машинного эпсилон.
Машинный ноль — числовое значение с таким отрицательным порядком, которое воспринимается машиной как ноль.
Машинная бесконечность - число, большее по модулю некоторого фиксированного для данного типа ЭВМ числа.
Машинным эпсилон
![]() называется относительная точность эвм,
то есть граница относительной погрешности
представления чисел в эвм.
называется относительная точность эвм,
то есть граница относительной погрешности
представления чисел в эвм.
Возьмем
 =
= и экспериментально найдем такое
приближенное целое значение n,
при котором значение
и экспериментально найдем такое
приближенное целое значение n,
при котором значение
 еще отлично от нуля.
еще отлично от нуля.
Аналогично
возьмем
 =
= ,
где m
значение, при котором не происходит
переполнение,
,
где m
значение, при котором не происходит
переполнение,
 ,
где k
значение, при котором сумма отлична от
1.
,
где k
значение, при котором сумма отлична от
1.
Результаты вычислительного эксперимента:
Машинная
бесконечность
 2^1019
2^1019
Машинный
нуль
 2^-1019
2^-1019
Машинное
эпсилон
 2^-52
2^-52
Листинг программы

Задача 1.3.
Задана функция
 .
Требуется вычислить значение функции
в точке
.
Требуется вычислить значение функции
в точке и
исследовать поведение погрешностей в
зависимости от погрешности аргумента.
и
исследовать поведение погрешностей в
зависимости от погрешности аргумента.
Решение задачи:
Пусть определитель
матрицы имеет вид
 Тогда, раскрывая определитель, получим
следующий вид функции: f(x)=2
Тогда, раскрывая определитель, получим
следующий вид функции: f(x)=2
Вычислим
определитель в точке![]() .
Для получения теоретической оценки
следует учесть, что величина для данного
варианта ∆ равна 0.0005. Производная
функции f’(x):=
.
Для получения теоретической оценки
следует учесть, что величина для данного
варианта ∆ равна 0.0005. Производная
функции f’(x):= монотонно возрастает, поэтому
монотонно возрастает, поэтому
max|f’(x)|:= 4364.475253887на интервале значений (х0-∆)<=(хо+∆).
Введем функцию
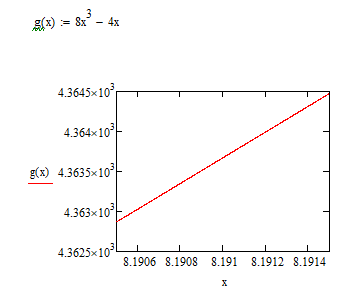
Таким образом,
теоретическая оценка получена:
![]() сравним теоретическую оценку с
погрешностью, полученной с помощью
вычислительного эксперимента.
сравним теоретическую оценку с
погрешностью, полученной с помощью
вычислительного эксперимента.

Полученные значения укладываются в теоретическую оценку погрешности. Заметим, что величина относительной погрешности невелика, например, в последнем эксперименте:

Ответ:
f(8.191)=
(306377±112)
результат содержит 3 верные цифры,
относительная погрешность 4*
Лабораторная работа № 1
по Математическим методам моделирования физических процессов
Студент Горьков И.А.
Группа ТФ-10-20
Вариант 19
Преподаватель Крупин Г.В.




