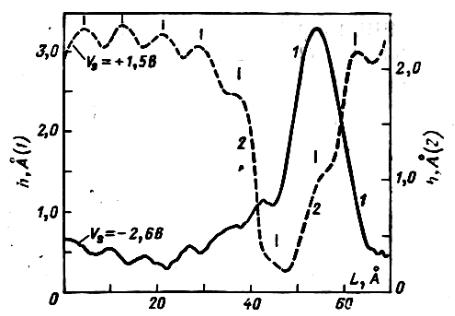
Кислород имеет 2р-состояния, которые лежат ниже ЕF для GaAs. В результате этого в полупроводниках n-типа адсорбированный атом кислорода имеет отрицательный заряд. Возникающий на поверхности отрицательный заряд приводит к изгибу зон вблизи поверхности и, непосредственно над уровнем Ферми появляется щель в спектре плотности состояний. Можно было думать о том, что поперечный размер области, в которой существенен изгиб зон, весьма мал и составляет величину порядка электронного радиуса 2р-оболочки кислорода.
Рис. 8.28. СТМ изображение адсорбированного атома кислорода на поверхности GaAs n-типа, полученное при различ-
ных напряжениях на образце
На самом деле, область, где важен изгиб зон, определяется характерным радиусом действия потенциала, создаваемого отрицательным зарядом, сосредоточенным около адсорби-
рованного атома кислорода, т.е. длиной дебаевского экранирования:
|
|
|
|
|
|
|
|
|
E |
|
/ kT |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
F |
2 |
|
|
|
|
2 e2n |
|
|
|
|
|
|
|
|
|
LD |
|
|
2 |
|
|
|
, |
(8.10) |
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
E |
|
|
/ kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
где Фm(EF/kT) – фермиевский интеграл порядка m. Отсюда для концентрации Si ~ 1018 см-3 LD ~ 56 Å. Об этом свидетельствуют изображения атомов кислорода, полученные с помощью СТМ и имеющие характерный размер ~ 50 Å.
Иная ситуация, если мы имеем GaAs p-типа. В этом случае адсорбированный кислород электронейтрален, поэтому изгиб зон отсутствует. В этом случае адсорбированные атомы кислорода существуют в виде выступов. Поперечный размер атомов кислорода, равный 5 – 10 Å, указывает на отсутствие дебаевского экранирования. Этот простой пример показывает, какую важную роль играет локальная плотность состояний при исследовании адсорбции методом СТМ.
8.3.4. Реконструируемые поверхности
Благодаря изобретению СТМ стало возможным изучать так называемую реконструируемую поверхность Si (111) – (7x7). Как эта поверхность образуется? После того, как кристалл Si выращен или разрезан, поверхностные атомы кремния перестраиваются (реконструируются) и их пространственное расположение отличается от того, которое они занимали в объеме кристалла. Реконструкция поверхности Si давно привлекала как теоретиков, так и экспериментаторов. Однако построенные теоретиками модели только недавно подтверждены экспериментально благодаря развитию метода СТМ.
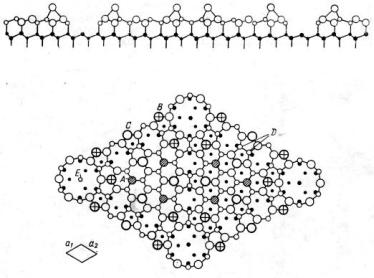
Элементарная ячейка Si (111)–(7x7) достаточно сложна и содержит 102 атома. Реконструируемая поверхность Si уст-
роена следующим образом. (На рис. 8.29 представлена модель, подтвержденная экспериментом).
На верхнем слое элементарной ячейки имеется 12 адатомов, каждый из которых связан с тремя атомами первого поверхностного слоя (1х1), которые в свою очередь образуют связь с тремя атомами нижележащего димерного слоя. В результате атомы имеют одну «болтающуюся» связь (dangling bond), а непосредственно связанные с ним атомы поверхностного слоя не имеют «болтающихся» связей. «Болтающиеся» связи существуют также на 6 атомах первого поверхностного слоя (rest – атомы), не связанных непосредственно с адатомами. В углах элементарной ячейки (7х7) отсутствуют атомы первого поверхностного слоя. При этом образуется ямка с «болтающейся» связью (одна на элементарную ячейку). Имеются также димерные цепи по бокам элементарной ячейки и вдоль малой диагонали. Таким образом, в каждой элементарной ячейке реконструированной поверхности Si (111)–(7x7) имеется 19 электронов, образующих «болтающиеся» связи, которые создаются 12 атомами, 6 rest-атомами и одной угловой ямкой. В результате экспериментов с помощью СТМ на поверхности Si (111)–(7x7) было показано, что различные атомы реконструированной поверхности не являются химически эквивалентными.
Изучение топографической структуры поверхности Si (111)–(7x7) после реакции с NH3 показало, что химические связи в первую очередь образуются за счет «болтающихся» связей, а не за счет разрыва валентных связей Si – Si. Более реакционно способны rest-атомы. Непрореагировавших rest-атомов почти нет. Дело в том, что «болтающиеся» электроны на атомах значительно более локализованы, чем rest-атомы, вследствие сильного взаимодействия с атомами второго поверхностного слоя, лежащими непосредственно под атомами, поэтому реакционная способность их меньше.
Рис. 8.29. Модель реконструируемой поверхности Si (111)
– (7 x 7):
атомы В – (угловые) и С (центральные), А – rest-атомы, D – димеры, Е – угловая ямка
8.4. Использование СМАС для изучения биологических структур
Основными преимуществами метода атомно-силовой микроскопии, используемого для изучения биологических структур, являются:
1)возможность изучения реальной поверхности клетки без применения специальных методов подготовки образцов (напыления металлов, приготовление реплик и пр.);
2)возможность проведения исследований живых бактерий на воздухе или в различных жидких средах;
3)высокое пространственное разрешение (доли нанометра в плоскости образца и сотые доли нанометра по нормали
кобразцу);
444
4) одновременное изучение с субнанометровым пространственным разрешением локальных свойств клеточной стенки, в том числе жесткости, пластичности и адгезивности.
В науке о биологических клетках – цитологии – ключевую роль играет прокариотическая микробная клетка – кишечная палочка или эшхерия (Escherichia). С помощью кишечной палочки изучены основные процессы, происходящие с клетками: рост, деление, деградация, бактериолиз и др.
Эшхерия или кишечная палочка – граммотрицательная микробная клетка семейства кишечных (рис. 8.30), имеет слегка вытянутую форму палочки с закругленными концами (0,4х0,8х1-3 мкм). В естественных условиях она подвижна, сбраживает глюкозу, лактозу и другие углеводы. Эшхерии – одни из наиболее типичных представителей микрофлоры кишечника млекопитающих. Культура эшхерии К12 используется в генной инженерии в качестве штаммов-носителей при передаче клонированных генов, контролирующих синтез интерферона, инсулина и ряда важных ферментов.
Для штамма К12 характерно наличие на поверхности бактериальной стенки длинных отростков-жгутиков. Жгутик представляет собой относительно жесткую спираль, состоящую только из белка – фагеллина. Кишечная палочка – подвижная бактерия, перемещение которой осуществляется с помощью жгутиков. Поверхность клеток имеет структурированную поверхность с периодом 50 нм и характерную для всех наблюдаемых штаммов.
На рис. 8. 31 представлено изображение стебелькового растения – обыкновенного укропа. Структурную основу стебелька составляют продольные и поперечные волокна. Продольные волокна имеют диаметр в несколько микрон. Атомносиловой микроскоп позволил увидеть структуру поперечных микроволокон укропа – фибрил, диаметр которых составляет 10-30 нм. Снимок сделан на свежем срезе стебелька. Этот экспериментальный факт показывает неограниченные возможнос ти атомно-силового микроскопа в изучении биологических
объектов в их активном состоянии в естественном окружении. Здесь мы видим только первые шаги, новые достижения еще впереди.
Рис. 8.31. Изображение одиночной бактерии кишечной палочки, осажденной на поверхность слюды. Размер изображения 3 х 2.5 мкм2. Изображение получено с помощью атомно-
силового микроскопа в режиме постоянной силы
Рис. 8.31. Изображение структуры поперечных волокон стебелька укропа. Размер кадра 1 х 1 мкм2
9. ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ 9.1. Основные понятия и единицы измерения
Теплопроводность конструкционных и функциональных материалов является характеристикой, имеющей существенное значение при конструировании многих аппаратов, приборов и при различных теплотехнических расчетах.
Развитие ряда направлений новой техники и общая тенденция к интенсификации рабочих процессов энергетических аппаратов связана, как правило, со значительным повышением рабочих температур и теплонапряженности деталей. Поэтому, легко объяснимым является значительный интерес, проявляемый к исследованиям теплопроводности в области умеренных и высоких температур. С другой стороны, многие работы в области физики твердого тела связаны с исследованием теплофизических свойств, в том числе и теплопроводности материалов при низких температурах.
За характеристику теплопроводности вещества принимают коэффициент пропорциональности в уравнении Фурье, описывающем процесс теплопередачи в теле.
где dQ — количество тепла, передаваемого за время d в направлении, перпендикулярном площадке поверхности S; dT/dx — градиент температур в направлении распространения теплового потока; — коэффициент теплопроводности вещества.
При этом в уравнении (9.1) коэффициент теплопроводности принимается постоянным в рассматриваемом узком интервале температур, а размеры поперечного сечения (площадка S) считаются также неизменными.

Знак «минус» в правой части уравнения указывает на отрицательное значение градиента температур, т. е. на понижение температуры в направлении распространения теплового потока.
При установившемся процессе тепловой поток и градиент температур не изменяются во времени и уравнение можно записать в виде
где q — тепловой поток в единицу времени через площадку S в перпендикулярном к ней направлении.
При неустановившемся режиме, когда величина теплового потока меняется во времени, изменяется во времени и температура в любой точке тела.
В общем случае (для потока тепла в трех направлениях X, Y, Z) такой процесс можно описать уравнением
|
dT |
|
|
|
|
2 |
t |
|
|
2 |
t |
|
|
2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(9.3) |
|
d |
с |
х |
2 |
у |
2 |
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где q — плотность вещества; с — удельная теплоемкость. Вещество при этом принимается изотропным и гомоген-
ным, а коэффициент теплопроводности — неизменным в данном температурном интервале.
Отношение называют температуропроводностью, которую
с
обычно обозначают буквой .
Температуропроводность характеризует скорость изменения температурного поля в веществе. Зная , с и , можно вычислить значение =а с .
Коэффициент теплопроводности в системе СИ имеет размерность вт/м град. Широкое распространение в литературе имеют также внесистемные единицы ккал/м ч град и кал!см сек град.
Теплопроводность металлов в значительной степени обусловлена переносом тепловой энергии электронами проводимости, что находит свое отражение во взаимосвязи между теплопроводностью и электропроводностью металлов. Указанная связь устанавливается законом Видемана — Франца
где e— теплопроводность (электронная); k — постоянная Больцмана; е — заряд электрона; Т – температура. L — число Лоренца.
Закон Видемана — Франца хорошо подтверждается для многих чистых металлов при Т (температура Дебая). Однако, у ряда металлов и в особенности у сплавов в процессе переноса тепловой энергии существенную роль играют также фононы (тепловые колебания решетки). Роль фононов тем больше, чем больше электрическое сопротивление металла (сплава). В этом случае число Лоренца, вычисленное на основании экспериментальных данных, сильно отличается от теоретического.
По предложению Кенигсбергера теплопроводность в этом случае представляют в виде аддитивной суммы составляющих — решеточной р и электронной е.
Для электронной составляющей теплопроводности можно общее тепловое сопротивление W=1/, аналогично электрическому сопротивлению, рассматривать как результат аддитивного сложения сопротивлений, обусловленных колеба-

ниями решетки Wi и примесями (химическими и физическими)
Wr,
Для низких температур (T<0,1 ) обычно принимают |
|
Wi = Т2 и Wr = B/T. |
(9.6) |
Уравнение описывает зависимость = f(T) в виде кривой с максимумом в области низких температур. Величина и положение максимума теплопроводности зависят от чистоты металла. Повышение чистоты приводит к увеличению максимального значения и к перемещению максимума в сторону низких температур. При более высоких температурах член уравнения Т2 должен принять вид сложной функции, содержащей интеграл Блоха и при T>> электронная составляющая теплопроводности не будет зависеть от температуры.
Решеточная теплопроводность делается существенно заметной в материалах, обладающих значительным электрическим сопротивлением, обусловленным дополнительным рассеянием электронов, как это, например, имеет место в полупроводниках и диэлектриках, В этом случае уменьшается рассеивание фононов на электронах проводимости, которые сами испытывают значительное сопротивление, и решеточная составляющая теплопроводности относительно возрастает.
9.2. Методы определения теплопроводности
Методы определения теплопроводности можно подразделить на стационарные (теплопроводность определяется в условиях установившегося, стационарного, теплового режима) и динамические (исследования проводятся при неустановившемся тепловом режиме).