Учебники 80349

расчетом, чтобы она позволяла обнаружить и по возможности исправить любые нарушения. При этом надо различать следующие виды ошибок результата:

1)возникающие из-за погрешностей в исходных данных;

2)обусловленные методическими погрешностями;

3)появляющиеся из-за возникновения неисправностей

в работе машины.

Первые два вида ошибок не являются объектом для работы системы контроля. Погрешности перевода или представления числовой информации в разрядной сетке автомата приведут к возникновению погрешности в результате решения задачи. Эту погрешность можно заранее рассчитать и, зная ее максимальную величину, правильно выбрать длину разрядной сетки машины. Методические погрешности также учитываются предварительно.

Проверка правильности функционирования отдельных устройств машины и выявление неисправностей может осуществляться по двум направлениям:

профилактический контроль, задача которого

–предупреждение появления возможных ошибок в работе;

оперативный контроль, задача которого – проверка правильности выполнения машиной всех операций.

Решение всех задач контроля становится возможным

только при наличии определенной избыточности информации.

отнести следующие приемы. В ЭВМ первого и второго поколения отсутствие системы оперативного контроля приводило к необходимости осуществления «двойного счета», когда каждая задача решалась дважды и в случае совпадения ответов принималось решение о правильности

81

функционирования ЭВМ.

Если в процессе решения какой-то задачи вычисляются тригонометрические функции, то для контроля можно использовать известные соотношения между этими функциями, например, sin2 + cos2 = 1. Если это соотношение выполняется с заданной точностью на каждом шаге вычислений, то можно с уверенностью считать, что ЭВМ работает правильно.

Вычисление определенного интеграла с заданным шагом интегрирования можно контролировать сравнением полученных при этом результатов с теми результатами, которые соответствуют более крупному шагу. Такой «сокращенный» алгоритм даст, видимо, более грубые оценки и по существу требует дополнительных затрат машинного времени.

Все рассмотренные примеры свидетельствуют о том, что такие методы контроля позволяют лишь зафиксировать факт появления ошибки, но не определяют место, где произошла эта ошибка. Для оперативного контроля работы ЭВМ определение места, где произошла ошибка, т. е. решение задачи поиска неисправности, является весьма существенным вопросом.

3.3.1. Основные понятия теории кодирования

Задача кодирования информации представляется как некоторое преобразование числовых данных в заданной системе счисления. В частном случае эта операция может быть сведена к группированию символов (представление в виде триад или тетрад) или представлению в виде символов (цифр) позиционной системы счисления. Так как любая позиционная система не несет в себе избыточности информации и все кодовые комбинации являются разрешенными, использовать такие системы для контроля не представляется возможным.

Систематический код – код, содержащий в себе кроме информационных контрольные разряды.

82

В контрольные разряды записывается некоторая информация об исходном числе. Поэтому можно говорить, что систематический код обладает избыточностью. При этом абсолютная избыточность будет выражаться количеством контрольных разрядов k, а относительная избыточность – отношением k/n , где n = m + k – общее количество разрядов в кодовом слове (m – количество информационных разрядов).

Понятие корректирующей способности кода обычно связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Если имеем n-разрядный код и вероятность искажения одного символа p, то вероятность того, что искажены k символов, а остальные n - k символов не искажены, по теореме умножения вероятностей будет

w = pk(1–p)n-k .

Число кодовых комбинаций, каждая из которых содержит k искаженных элементов, равна числу сочетаний из n по k:

Тогда полная вероятность искажения информации

Так как на практике p = 10-3 ...10-4, наибольший вес в сумме вероятностей имеет вероятность искажения одного символа. Следовательно, основное внимание нужно обратить на обнаружение и исправление одиночной ошибки.

Корректирующая способность кода связана также с

83

понятием кодового расстояния.

Кодовое расстояние d(A, В) для кодовых комбинаций А и В определяется как вес третьей кодовой комбинации, которая получается поразрядным сложением исходных комбинаций по модулю 2.

Вес кодовой комбинации V(A) – количество единиц, содержащихся в кодовой комбинации.

Коды можно рассматривать и как некоторые геометрические (пространственные) фигуры. Например, триаду можно представить в виде единичного куба, имеющего координаты вершин, которые отвечают двоичным символам (рис. 3.7). В этом случае кодовое расстояние воспринимается как сумма длин ребер между соответствующими вершинами куба (принято, что длина одного ребра равна 1). Оказывается, что любая позиционная система отличается тем свойством, что минимальное кодовое расстояние равно 1 (рис. 3.8а).

Рис. 3.7. Геометрическое представление кодов

В теории кодирования показано, что систематический код способен обнаружить ошибки только тогда, когда минимальное кодовое расстояние для него больше или равно

2t, т. е.

dmin 2t,

84

где t – кратность обнаруживаемых ошибок (в случае одиночных ошибок t = 1 и т. д.).

Это означает, что между соседними разрешенными кодовыми словами должно существовать по крайней мере одно кодовое слово (рис. 3.8б,в).

Рис. 3.8. Кодовые расстояния

В тех случаях, когда необходимо не только обнаружить ошибку, но и исправить ее (т. е. указать место ошибки), минимальное кодовое расстояние должно быть

dmin 2t+1.

Существуют коды, в которых невозможно выделить абсолютную избыточность. Неявная избыточность характерна также для кодов типа «k из n». Примером является код «2 из 5», который часто используется для представления информации. Суть его в том, что в слове из пяти разрядов только два разряда имеют единичное значение.

85

3.3.2. Методы эффективного кодирования информации

Информационную избыточность можно ввести разными путями. Рассмотрим один из путей эффективного кодирования.

В ряде случаев буквы сообщений преобразуются в последовательности двоичных символов. Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии шума позволит уменьшить время передачи.

Такое эффективное кодирование базируется на основной теореме Шеннона для каналов без шума, в которой доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.

Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каждый символ должен принимать значения 0 и 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.

При отсутствии статистической взаимосвязи между буквами конструктивные методы построения эффективных кодов были даны впервые К.Шенноном и Н. Фано. Их методики существенно не различаются, поэтому соответствующий код получил название кода Шеннона-Фано.

Код строится следующим образом: буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним – 0. Каждая из полученных групп, в свою очередь, разбивается на две

86

подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.

Рассмотрим алфавит из восьми букв (табл. 3.4). Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется три символа.

Таблица 3.4 Кодирование по методике Шеннона-Фано

Вычислим энтропию набора букв:

и среднее число символов на букву

8

lcp = - p(zi) n(zi) 2,84,

i 1

где n(zi) – число символов в кодовой комбинации,

соответствующей букве zi.

Значения zi и lcp не очень различаются по величине. Рассмотренная методика Шеннона-Фано не всегда

приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу.

Множество вероятностей в предыдущей таблице можно было разбить иначе (табл. 3.5).

87

Таблица 3.6

Кодирование по методике Хаффмена

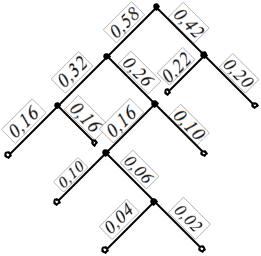
Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь перехода сообщений по строкам и столбцам таблицы. Для наглядности строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ 1, а с меньшей – 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до каждой буквы (рис.

3.9).

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию (табл. 3.7.).

89

3.3.3. Кодирование по методу четности-нечетности

Если в математическом коде выделен один контрольный разряд (k = 1), то к каждому двоичному числу добавляется один избыточный разряд и в него записывается 1 или 0 с таким условием, чтобы сумма цифр в каждом числе была по модулю 2 равна 0 для случая четности или 1 для случая нечетности. Появление ошибки в кодировании обнаружится по нарушению четности (нечетности). При таком кодировании допускается, что может возникнуть только одна ошибка. В самом деле, для случая четности правильной будет только половина возможных комбинаций. Чтобы одна допустимая комбинация превратилась в другую, должно возникнуть по крайней мере два нарушения или четное число нарушений. Пример реализации метода

90