
Квантовая механика в задачах и вопросах. Шушлебин И.М., Янченко Л.И
.pdf
ˆ 2* |
* |
эрмитовость . |
2M |
1dv |
Задача 4. Проверить правила коммутации в равенствах
ˆ |
ˆ |
|
|
|
ˆ |
i y. |
|
|
|
||
[x, MX ] 0; [y, MX ] |
|
i z; [z, MX ] |
|
|
|
||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
1) [x, MX ] |
i x z |
|
y |
y |
z |
i z |
y |
y |
z |
x 0. |
|
|
|
|
|
|
|
|
|||||
В данном выражении нет дифференциала по переменной х.
2) |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[y, MX ] |
yi |
z |
y |
y |
|
z |
|
i |
z |
|
|
y |
y |
|
z |
y |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
i yz |
|
y2 |
|
|
z |
|
y |
|
y2 |
|
|
zy |
|
|
|
|
|
|
|
i z. |
||||||||||||
|
y |
z |
|
y |
z |
|
y |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3) |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[z, MX ] |
zi |
z |
|
y |
y |
|
z |
|
i |
z |
|
|
y |
y |
|
z |
|
z |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
i z2 |
|
|
yz |
|
|
|
z2 |
|
|
|
|
|
|
y yz |
|
|
|
|
|
|
|
i y. |
|
|
|
|||||||
|
|
y |
|
z |
y |
|
|
z |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Задача 5. Доказать, что оператор кинетической энергии
ˆ |
ˆ 2 |
. |
T коммутирует с M |
||
21

Решение.
|
|
|
ˆ 2 |
|
|
ˆ |
ˆ |
ˆ |
M |
ˆ |
|
Оператор T представим в виде T |
Tr |
2mr |
. Tr |
не зави- |
|
|
|
|
|
|
|
сит от |
и |
|
, следовательно, коммутирует с |
ˆ |
2 |
|
|
|||||||||
|
M . |
|
|
|||||||||||||
Оператор кинетической энергии трансверсального дви- |
||||||||||||||||
жения |
отличается |
от |
|
ˆ 2 |
только на |
независящий |
от и |
|||||||||
M |
||||||||||||||||
множитель |
1 |
|
, а каждый оператор коммутирует сам с собой. |
|||||||||||||
|
|
|
||||||||||||||
|
|
|
2mr |
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ˆ ˆ 2 |
ˆ |
ˆ 2 |
1 |
ˆ |
2 |
ˆ 2 |
0 . |
|
|
|
|
||||
[T, M ] [Tr , M ] |
|
|
[M , M ] |
|
|
|
|
|||||||||
|
2mr |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 6. Проверить правило коммутации |
|
|
||||||||||||||
|
ˆ |
ˆ |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
[MX ,MY ] |
|
i MZ . |
|
|
|
|
|
|
|
|
|
|
||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ˆ |
ˆ |
|
ˆ |
ˆ |
|
ˆ |
ˆ |
|
ˆ |
ˆ |
|
ˆ |
ˆ |
|
|
[MX ,MY ] |
|
MXMY MYMX |
(yPz |
zPy )(zPx |
x Pz ) |
|||||||||||
|
ˆ |
|
|
ˆ |
ˆ |
|
ˆ |
|
ˆ |
ˆ |
2 ˆ ˆ |
|
ˆ ˆ |
|
||
|
(zPx |
|
x Pz )(yPz |
zPy ) |
yPz |
zPx |
z PyPx |
yxPxPx |
||||||||
|
ˆ ˆ |
|
ˆ ˆ |
|
ˆ ˆ |
2 |
ˆ ˆ |
ˆ |
ˆ |
|
ˆ |
ˆ |
||||
|
zxPyPz |
zyPxPz |
yxPzPz |
z PxPy |
xPz |
zPy |
yPz |
zPx |
||||||||
|
ˆ |
|
ˆ |
|
|
ˆ ˆ |
|
ˆ |
ˆ |
|
ˆ |
ˆ |
ˆ |
i |
ˆ |
|
|
xPz |
zPy |
|
zxPyPz |
|
zyPxPz |
[z,Pz ](xPy |
yPx ) |
MZ |
|||||||
22
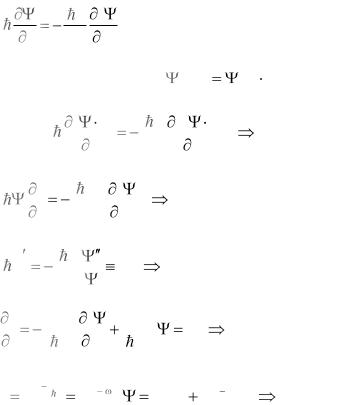
Практическое занятие № 4
Задача 1. Найти решение временного уравнения Шредингера для свободной частицы массы m, движущейся с импульсом р в положительном направлении х.
Решение.
Потенциальную энергию частицы можно считать равной нулю (U = 0) и уравнение Шредингера будет иметь вид
22
it 2m x2 .
Разделяем переменные: (x, t) (x) f (t).
Имеем i |
|
( f ) |
|
2 |
|
2 ( |
f ) |
|
||||||||||||||
|
|
|
t |
|
|
2m |
|
x2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
f |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||
i |
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
t |
2m |
|
x2 |
|
|
|
||||||||||||
|
|
|
f |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
i |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
||||||
|
|
f |
|
|
|
2m |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
f |
|
|
i E f; |
2 |
|
|
|
2m E |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||
|
|
|
|
|
|
|
x2 |
|
||||||||||||||
|
|
t |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
f |
|
|
|
c e i E t |
|
|
c e i t ; c eikx |
c e ikx |
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|||||
23

(k2 2m E;c |
0 в положительном направлении х) |
|
2 |
3 |
|
(x, t) |
cei(kx |
t) . |
Полученное выражение соответствует плоской волне де Бройля.
*
 2 c c* const.
2 c c* const.
Местонахождение такой частицы равновероятно во всех точках пространства.
Задача 2. В некоторый момент времени частица находится в состоянии, описываемом - функцией, где А и а – неизвестные постоянные. Найти средние значения 1) координаты х; 2) проекции импульса рх.
Решение.
1) x |
|
|
x2 |
|
x2 |
|
x |
* |
dx A*A x e a2 |
e ikx e a2 |
eikxdx |
||
|
2x2 |
|
|
|
|
|
A*A |
x e a2 |
dx |
0. |
|
|
|
Поскольку подынтегральная функция нечетная (из-за присутствия х). Аналогично и для плоской Волны де Бройля.
2) px |
*pˆ x dx i |
* |
|
dx |
|
x |
|||
|
|
|
|
24
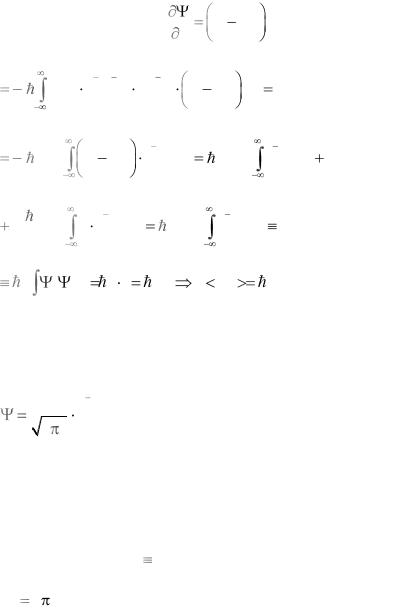
Воспользуемся заменой |
|
|
|
|
ik |
2x . |
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x |
|
a2 |
|
|
|
|
x2 |
|
x2 |
|
|
2x |
|
||
|
i A*A e ikx a2 |
eikx |
|
|
|
|
|||||
a2 |
ik |
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
i A*A ik 2x |
2x2 |
|
|
|
2x2 |
|||||
|
e a2 |
dx kA*A e a2 dx |
|||||||||
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
2i A*A |
2x2 |
|
|
|
|
|
|
2x2 |
||
|
x e a2 dx kA*A e a2 dx |
||||||||||
|
a2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
k * dx k 1 k |
p |
x |
k. |
|
|
|
Задача 3. Частица находится в сферическом симметричном поле в состоянии, описываемом нормированной волновой функцией
|
1 |
|
e r/a |
|
|
|
r , |
|
|
|
|
|
2 a |
где r – расстояние от центра поля, а – постоянная. Найти
<r>.
Решение.
В данном случае dq dV . В качестве dV выбираем бесконечно тонкий сферический слой с радиусами r и r+dr. Для него dV 4 r2dr . Отсюда следует
25
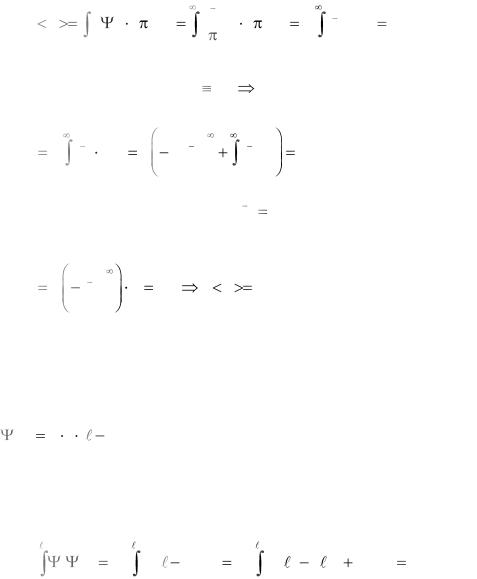
|
|
|
|
2 |
2 |
|
|
e 2r/a |
3 |
2 |
|
2r/a |
|
|
|
|
|
|
|
|
|||||||
r |
r |
|
|
|
4 r |
dr |
|
|
4 r dr |
|
e |
|
rdr |
|
|
|
|
2 ar2 |
a |
|
|||||||
|
|
|
|
|
|
|
0 |
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Введем переменную |
2r |
y |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
e y ydy |
a |
ye y |
|
e ydy |
||
2 |
0 |
|
2 |
|
0 |
0 |
|
Используем тот факт, что |
ye y |
0 при у = 0 и у = ∞, в |
|||||
итоге получаем |
|
|
|
|
|
||
a |
|
a |
a |
|
a . |
||
e y |
|
r |
|||||
2 |
|
0 |
2 |
2 |
|
|
2 |
Практическое занятие № 5
Задача 1. Найти среднюю кинетическую энергию частицы в одномерной потенциальной яме с глубиной U = ∞ и шириной 0 ≤ x ≤ ℓ, если частица находится в состоянии
(x) A x ( x) .
Решение.
Проведем нормировку волновой функции.
* dx |
A2 x2 ( |
x)2dx A2 (x2 2 2 x3 x4 )dx |
0 |
0 |
0 |
26
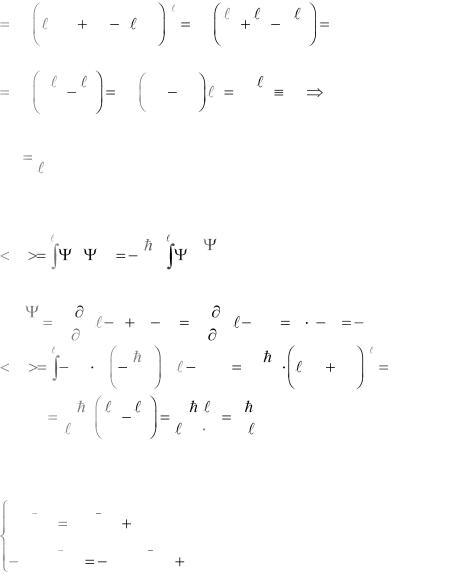
2 |
2 x3 |
x5 |
|
x4 |
|
2 |
5 |
5 |
|
|
5 |
|||
A |
|
|
|
2 |
|
A |
|
|
|
|
|
|
2 |
|
3 |
5 |
4 |
|
3 |
5 |
|
4 |
|||||||
|
|
0 |
|
|
|
|||||||||
A2 |
8 5 |
5 |
|
A2 16 15 |
|
5 |
|
A2 5 |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
15 |
2 |
|
|
30 |
30 |
|
|
|
30 |
|
|
|
|
A2 305 .
Средняя кинетическая энергия
|
ˆ |
2 |
|
|
d2 |
|
K |
K dx |
|
|
|
|
dx; |
2m |
0 |
dx2 |
||||
|
0 |
|
|
|
|
|
|
d2 |
|
|
A |
|
|
[ |
|
x |
|
x( 1)] |
A |
|
( |
|
|
2x) |
A ( 2) |
|
2A; |
|||||||||||||
|
dx2 |
|
|
x |
|
|
x |
|
|
|
|||||||||||||||||||||||
|
K |
|
|
|
|
2A A |
|
|
2 |
|
|
|
x( |
x)dx |
|
|
A2 2 |
x2 |
x3 |
|
|
||||||||||||
|
0 |
|
2m |
|
|
|
m |
2 |
3 |
|
0 |
||||||||||||||||||||||
|
|
|
|
|
30 2 |
|
3 |
|
|
|
3 |
|
|
30 2 |
3 |
|
|
5 2 |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
5m |
2 |
|
3 |
|
|
|
|
|
|
5m 6 |
m 2 |
|
|
|
|
|||||||||||
Задача 2. Из уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
k2d |
|
|
|
|
|
|
ik1d |
|
|
|
|
|
|
|
ik1d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A e |
2 |
|
|
|
A |
e |
2 |
|
|
B e 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k2d |
|
|
|
|
|
|
|
|
|
|
ik1d |
|
|
|
|
ik1d |
|
|
|
|
|
||||||
|
k2A e |
2 |
|
|
|
ik A |
e |
2 |
|
|
ik B e 2 ; |
|
|
|
|
||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||||
27
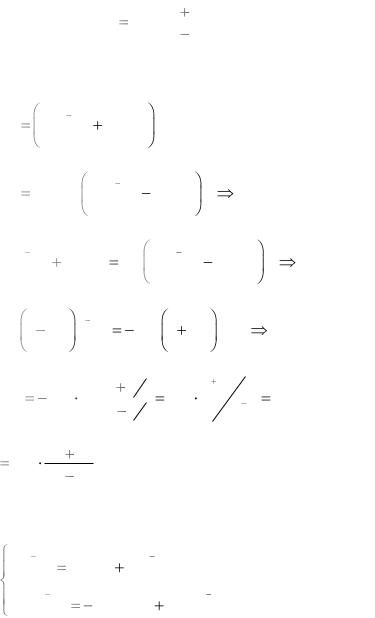
показать, что |
A2 |
|
eik1d |
ik1 |
|
|
|
k2 |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
ik |
|
|
|
k |
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
ik1d |
|
|
|
|
ik1d |
|
|
|
|
k2d |
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
|
A e |
2 |
|
|
|
B e 2 |
e 2 |
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
ik1 |
|
|
k2d |
|
|
|
|
ik1d |
|
|
|
|
|
|
ik1d |
|
|
|
|
|
|
|
|
|
||||||||||||||||
A |
|
|
e 2 |
|
|
|
|
A e |
2 |
|
|
|
|
|
B e 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1 |
|
|
k2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
ik1d |
|
|
|
ik1d |
|
ik1 |
|
|
|
|
|
|
|
|
|
|
|
ik1d |
|
|
|
|
|
|
|
ik1d |
|
||||||||||||||
A e 2 B e 2 |
|
|
A |
e |
2 |
|
|
|
|
B e 2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
k2 |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ik1 |
|
|
|
|
|
|
|
ik1d |
|
|
|
|
|
ik1d |
|
|
|
|
|
ik1 |
|
|
|
|
|
|
|||||||||||||
A 1 |
|
|
|
e 2 |
|
e 2 |
1 |
|
|
|
B |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2 |
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
ik d |
|
|
|
|
ik d |
ik |
|
|
|
|
|
|
|
|
|
|
|
k2 |
ik1 |
||||||||||||||||||
|
A2 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
e 2 |
|
e |
2 |
|
k2 |
|
|
|
|
eik1d k2 ik1 k2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
ik |
|
|
|
|||||||||||||||||||||||||||||||||||
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
||||||||||||
eik1d ik1 k2 . ik1 k2
Задача 3. Из системы уравнений
|
|
|
k2d |
|
|
|
ik1d |
|
|
|
|
ik1d |
|
|
|
|
|
B e |
2 |
|
|
A |
e 2 |
B e |
2 ; |
|
|
|
|||||||
3 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
k2d |
|
|
|
|
|
ik1d |
|
|
|
|
ik1d |
|
k |
B e 2 |
|
ik A |
e 2 |
ik B e 2 |
; |
|||||||||||
2 |
|
3 |
|
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|||
28
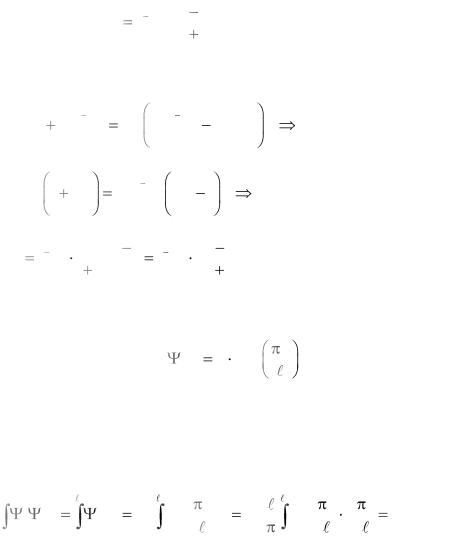
получить, что |
A2 |
e ik1d |
ik1 |
k2 |
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
B |
|
|
|
|
ik |
k |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ik1d |
|
|
ik1d |
|
ik1 |
|
|
|
|
|
ik1d |
|
|
|
|
ik1d |
|||||
A e 2 |
B e 2 |
|
|
B e |
2 |
|
|
|
A e 2 |
|||||||||||||
|
|
|
|
|||||||||||||||||||
2 |
|
2 |
|
|
|
|
k2 |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A eik1d |
|
ik1 |
|
|
|
|
|
ik1d |
|
|
ik1 |
|
|
|
|
|
|
|
|
|||
1 |
|
|
B e 2 |
|
|
|
1 |
|
|
|
|
|||||||||||
2 |
|
|
k2 |
|
|
2 |
|
|
|
|
k2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A2 e ik1d ik1 / k2 |
1 |
e |
ik1d |
ik1 |
k2 |
. |
||||||||||||||||
|
|
|
|
|||||||||||||||||||
B2 |
|
1 ik1 / k2 |
|
|
|
|
|
|
ik1 |
k2 |
||||||||||||
Задача 4. В одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (0 ≤ x ≤ b) нахо-
дится частица в состоянии |
(x) A sin2 |
x |
. Определить |
|
вероятность пребывания частицы в основном состоянии.
Решение.
Найдем нормировочный коэффициент А.
* dx |
2dx A2 sin4 |
x |
dx A2 |
|
sin4 |
x |
d |
x |
|
|
|
|
|||||
0 |
0 |
|
|
0 |
|
|
|
|
29
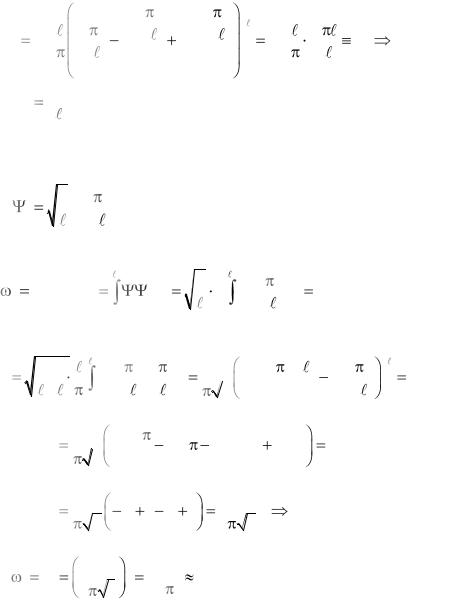
|
A2 |
|
|
3 |
x |
|
sin |
x |
|
|
sin 4 |
x |
|
A2 |
3 |
|
1 |
||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
8 |
|
4 |
32 |
|
0 |
8 |
|
|
||||||||||
A2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Собственная функция основного состояния (n = 1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin |
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность пребывания частицы в состоянии с n = 1 бу- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дет |
|
c2 , где c |
|
|
|
|
|
|
|
dx |
|
2 A sin3 |
x |
dx |
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos3 ( x/ ) |
|
|
|
|
|||||||||
|
|
2 8 |
|
|
|
|
|
|
sin3 |
x |
d( |
|
|
x) |
4 |
|
|
|
cos |
x |
|
|
|||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
0 |
||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
cos3 |
|
|
|
|
cos |
|
|
|
1 cos3 0 |
cos 0 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
4 |
|
|
1 |
1 |
|
1 |
|
1 |
|
|
|
|
16 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
16 |
2 |
256 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
c2 |
|
|
|
|
|
|
0,96 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
1 |
|
|
3 |
|
|
3 |
|
|
27 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
30
