
- •Введение
- •1. Теория колебаний
- •1.1. Устойчивость положения равновесия
- •1.1.1. Определение устойчивости положения равновесия
- •1.1.2. Теорема Лагранжа–Дирихле
- •1.2. Колебания системы с одной степенью свободы
- •1.2.1. Собственные линейные колебания системы
- •Дифференциальное уравнение собственных линейных колебаний системы
- •Интегрирование дифференциального уравнения собственных колебаний
- •1.2.2. Влияние линейного сопротивления на малые собственные колебания системы с одной степенью свободы
- •Интегрирование дифференциального уравнения движения
- •Затухающие колебания
- •Затухающие движения
- •1.2.3. Вынужденные колебания системы без учета сопротивления
- •Основные свойства вынужденных колебаний
- •Исследование вынужденных колебаний
- •Общие свойства вынужденных колебаний
- •Основы виброзащиты
- •1.3. Математический и физический маятники
- •1.4. Малые колебания системы с двумя степенями свободы (результат для общего случая)
- •1.4.1. Кинетическая энергия
- •1.4.2. Потенциальная энергия
- •1.4.3. Диссипативная функция
- •1.4.4. Дифференциальные уравнения собственных колебаний
- •1.4.5. Интегрирование дифференциальных уравнений. Уравнение частот
- •1.4.6. Главные координаты
- •1.4.7. Влияние линейного сопротивления на собственные колебания
- •1.4.8. Вынужденные колебания без учета сопротивления
- •1.4.9. Влияние линейного сопротивления на вынужденные колебания
- •2. Теория удара
- •2.1. Основные положения и понятия теории удара
- •2.2. Теоремы об изменении количества движения и о движении центра масс для удара. Теорема Кельвина
- •2.3. Теорема об изменении кинетического момента при ударе
- •2.4. Удар точки о неподвижную поверхность
- •2.4.1. Прямой удар
- •2.4.2. Косой удар
- •2.4.3. Экспериментальное определение коэффициента восстановления
- •2.5. Теорема Карно
- •2.6. Удар двух тел
- •2.7. Центр удара
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
2.7. Центр удара
Е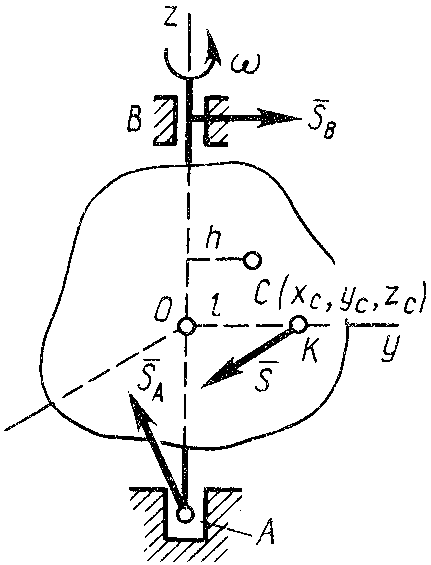 сли
по твердому телу, которое может вращаться
вокруг неподвижной оси, произвести
удар, приложив ударный импульс
,
то при выполнении некоторых условий не
возникнет ударных реакций в подшипниках
оси вращения. Получим эти условия.
сли
по твердому телу, которое может вращаться
вокруг неподвижной оси, произвести
удар, приложив ударный импульс
,
то при выполнении некоторых условий не
возникнет ударных реакций в подшипниках
оси вращения. Получим эти условия.
П
Рис. 27![]() ,
по которой направлена координатная ось
,
имеет до удара угловую скорость
(рис. 27). К телу приложен ударный импульс
;
угловая скорость изменяется и становится
равной
.
Освободив тело от связей и заменив их
импульсами реакций
,
по которой направлена координатная ось
,
имеет до удара угловую скорость
(рис. 27). К телу приложен ударный импульс
;
угловая скорость изменяется и становится
равной
.
Освободив тело от связей и заменив их
импульсами реакций
![]() и
и
![]() ,
применим к явлению удара теоремы об
изменении количества движения и
кинетического момента. Имеем
,
применим к явлению удара теоремы об
изменении количества движения и
кинетического момента. Имеем
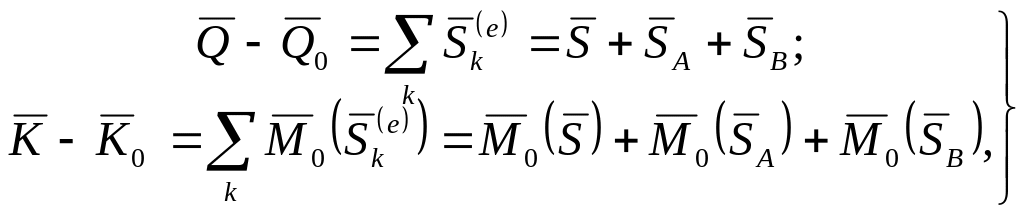 ,
(132)
,
(132)
где
![]() ,
,
![]() – количество движения и кинетический
момент после удара, а
– количество движения и кинетический
момент после удара, а
![]()
![]() – соответственно те же величины перед
ударом. Скорости точек при вращении
тела вычисляем по формуле Эйлера:
– соответственно те же величины перед
ударом. Скорости точек при вращении
тела вычисляем по формуле Эйлера:
![]() .
.
Следовательно, количество движения
![]()
где
– масса тела;
![]() – радиус-вектор центра масс. Так как
– радиус-вектор центра масс. Так как
![]() и
и
![]() направлены по оси вращения, то
направлены по оси вращения, то

![]() . (133)
. (133)
Проекции
кинетического момента на оси координат
можно определить по формулам для тела,
имеющего одну закрепленную точку, но
при условии, что
![]() и
и
![]() .
Имеем:
.
Имеем:
![]() ,
,
![]() ,
,
![]() .
.
Используя эти формулы, получим:
![]() ,
,
![]() , (134)
, (134)
![]() .
.
Проецируя (132) на оси координат и учитывая (133) и (134) получаем:
 . (135)
. (135)
Из
системы уравнений (135) определяем импульсы
реакций
и
![]() изменение угловой скорости при ударе
изменение угловой скорости при ударе
![]() для заданного тела и внешнего ударного
импульса
.
для заданного тела и внешнего ударного
импульса
.
Определим
условия, при которых удар по телу не
вызывает ударных реакций в подшипниках,
т.е. когда
![]() .
Из системы уравнений (135) в этом случае
получаем:
.
Из системы уравнений (135) в этом случае
получаем:
 . (136)
. (136)
Из
соотношений (136) следует: так как
![]() ,
то ударный импульс
находится в плоскости, параллельной
,
то ударный импульс
находится в плоскости, параллельной
![]() .
Выберем начало координат
на оси вращения так, чтобы импульс
лежал в плоскости
,
а координатную ось
направим параллельно
.
Тогда ударный импульс
пересечет ось
.
Выберем начало координат
на оси вращения так, чтобы импульс
лежал в плоскости
,
а координатную ось
направим параллельно
.
Тогда ударный импульс
пересечет ось
![]() в точке
в точке
![]() .
При таком выборе начала координатой
осей
.
При таком выборе начала координатой
осей
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
так как
параллелен
и пересекает
.
,
так как
параллелен
и пересекает
.
Учитывая
это, из условий (136) получаем из второго
уравнения
![]() ,
из четвертого
,
из четвертого
![]() ,
из пятого
,
из пятого
![]() ,
т.е. центр масс находится в плоскости
,
т.е. центр масс находится в плоскости
![]() и ось вращения
является главной осью инерции для точки
.
Так как ударный импульс
параллелен оси
,
то, следовательно, он перпендикулярен
плоскости
,
проходящей через ось вращения и центр
масс.
и ось вращения
является главной осью инерции для точки
.
Так как ударный импульс
параллелен оси
,
то, следовательно, он перпендикулярен
плоскости
,
проходящей через ось вращения и центр
масс.
Если
ввести длину
![]() ,
то
,
то
![]() при направлении
в положительную сторону оси
.
С учетом этого, исключая
из первого и шестого уравнений (136),
получаем
при направлении
в положительную сторону оси
.
С учетом этого, исключая
из первого и шестого уравнений (136),
получаем
![]() . (137)
. (137)
При
сделанном выборе осей координат
![]() – расстояние от оси вращения
до центра масс. Если его обозначить
,
то
– расстояние от оси вращения
до центра масс. Если его обозначить
,
то
![]() .
.
Получена формула, по которой вычисляется приведенная длина физического маятника.
Точка пересечения линии действия ударного импульса с плоскостью, проходящей через ось вращения и центр масс при отсутствии ударных реакций в подшипниках, называется центром удара. Любой по числовой величине ударный импульс , линия действия которого проходит через точку перпендикулярно плоскости, содержащей ось вращения и центр масс, не вызывает ударных реакций в подшипниках; если ось вращения является главной осью инерции для точки – точки пересечения оси вращения с перпендикулярной плоскостью, содержащей ударный импульс ; если расстояние от оси вращения до линии действия ударного импульса равно приведенной длине физического маятника; если центр удара и центр масс лежит по одну сторону от оси вращения.
Если
центр масс находится на оси вращения,
то
![]() и расстояние
от оси вращения до центра удара
равно бесконечности. В этом случае
центра удара не существует.
и расстояние
от оси вращения до центра удара
равно бесконечности. В этом случае
центра удара не существует.
Так
как для_ центра масс, находящегося на
оси вращения,
![]() ,
то
,
то
![]() и из первого уравнения (132) получаем
и из первого уравнения (132) получаем
![]() ,
,
откуда
![]() ,
,
т.е. ударный импульс, приложенный к телу, целиком передается на подшипники.
