1.4.7. Влияние линейного сопротивления на собственные колебания

Пусть и – главные координаты системы. Тогда квадратичные формы для кинетической и потенциальной энергии содержат квадраты своих переменных:

; . (83)

Диссипативная функция в общем случае сохраняет член с произведением даже для случая главных координат:

. (84)

Подставляя эти значения , и в уравнения Лагранжа (56), получаем следующую системы уравнений собственных колебаний с учетом линейного сопротивления:

(85)

Коэффициенты системы уравнений удовлетворяют условия

;

. (86)

Использование главных координат не приводит к распадению системы уравнений на независимые уравнения, но системы уравнений становиться несколько проще. Решение системы (85) можно искать в форме

; . (87)

Подставляя (87) в системы уравнений (85) и сокращая на , получаем

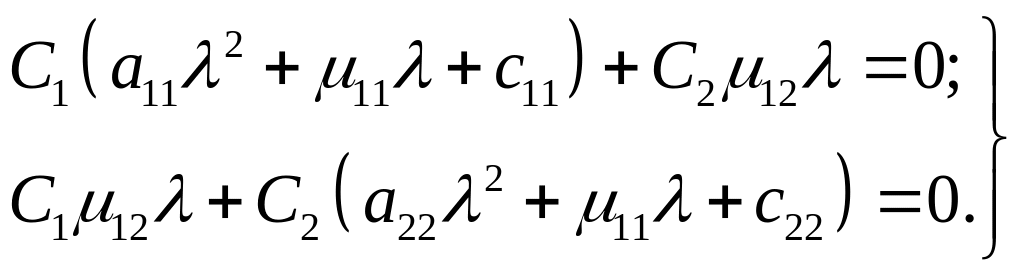(88)

Для того чтобы эта система однородных линейных уравнений относительно неизвестных , имела ненулевые решения, должен быть равен нулю определитель этой системы:

.

Получено характеристическое уравнение для , являющееся уравнением четвертой степени. В развернутом виде характеристическое уравнение имеет форму

(89)

Каждому из четырех его коней , , , соответствуют определенные значения постоянных и .

Из уравнения (88) определяются не величины и для каждого коня , а только их отношения:

,

(90)

Индекс указывает, для какого корня берутся постоянные и .

Не проводя подобного исследования, отметим, что при выполнении условий (86) возможны следующие варианты корней характеристического уравнения (89) и соответственно решений системы дифференциальных уравнений (85).

1. Корни комплексные.

Они попарно сопряжены, так как коэффициенты уравнения вещественны и имеют отрицательные вещественные части:

; .

Этот случай получается при малом сопротивлении. Подставляя эти значения в (87), после несложных преобразований получаем

;

.

Здесь все , , , – постоянные величины.

Каждая главная координата является суммой двух затухающий колебаний. Четыре из восьми постоянных определяются из начальных условий; другие четыре – через величины , .

2. Корни действительные.

Их можно представить в форме

; ,

Причем , . Для главных координат и в этом случае

Движение периодическое, затухающее. Оно получается при большом сопротивлении.

3. Два корня действительны, а два – комплексно-сопряженные:

; ,

Для и получаем

В этом случае имеем наложение затухающих колебаний на затухающее движение. Неглавные обобщенные координаты линейно выражаются через главное в соответствии с (72). Следовательно, для них каждая из обобщенных координат является линейной комбинацией рассмотренных трех видов движений. Аналогичное положение будет в случае любого конечного числа степеней свободы.

1.4.8. Вынужденные колебания без учета сопротивления

Рассмотрим вынужденные колебания системы с двумя степенями свободы без учета сопротивления под действием гармонических возмущающих обобщенных сил, отнесенных к главным координатам. Гармонические возмущающие силы для других координат можно привести к гармоническим возмущающим силам для главных координат, если частоты первоначальных возмущающих сил одинаковы. Действие возмущающих сил, имеющих разные частоты, следует рассматривать по отдельности, используя свойство суперпозиции решений линейных дифференциальных уравнений.

Итак, для главных координат   и из уравнения Лагранжа (56) получим следующую системы уравнений вынужденных колебаний:

; ,

Или после деления первого уравнения на , второго на

; . (91)

Здесь введены обозначения для постоянных: , – квадраты собственных частот; , – относительные амплитуды возмущающих сил.

Каждое уравнение системы (91) можно интегрировать независимо от другого уравнения. Общие решения этих уравнений, согласно теории дифференциальных уравнений, являются суммой общих решений уравнений без правых частей (собственные колебания) и частых решений уравнений с правыми частями (вынужденные колебания):

; .

Свойства собственных колебаний и уже рассмотрены. Они являются гармоническими колебаниями с частотами и . Рассмотрим вынужденные колебания и . Возможны следующие характерные случаи.

1. Частота возмущающей силы не совпадает ни с одной из частот собственных колебаний и . Тогда частные решения можно искать в форме

; .

Подставляя это в (91) и приравнивая нулю коэффициенты при синусах в полученных тождествах, имеем следующие уравнения для определения постоянных и :

; .

Отсюда

; . (92)

Вынужденные колебания через главные координаты выражаются в форме

; . (93)

Если обобщенные координаты не являются главными, то вынужденные колебания, согласно формулам перехода (72), будут линейной комбинацией (93).

2. Частота возмущающей силы совпадает с одной из частот собственных колебаний, например . Это случай резонанса на этой частоте. Решение для вынужденных колебаний можно искать в виде

; . (94)

Подставляя (94) в систему уравнений (91), получаем уравнения для определения постоянных и . Из этих уравнений находим

; . (95)

Вынужденные колебания для главных координат выражаются в форме

;

. (96)

По одной главной координате получаем резонанс.

Переходим к другим, не главным, обобщенным координатам по формулам перехода (72) приводит к резонансу по обеим координатам.

При получается резонанс по обеим главным координатам. Для системы с двумя степенями свободы резонанс наступает при совпадении частоты возмущающей силы с одной из двух частот собственных колебаний.

Для системы с степенями свободы для появления резонанса достаточно совпадения частоты возмущающей силы с одной из частот собственных колебаний.