
- •Введение
- •1. Дискретность (квантование)
- •2. Корпускулярно-волновой дуализм
- •3. Волновая функция свободно движущейся частицы
- •4. Принцип суперпозиции состояний. Волновой пакет
- •5. Статистическое толкование волновой функции
- •6. Свободная частица в ограниченном объеме пространства
- •7. Операторы физических величин
- •8. Собственные функции и собственные значения операторов
- •9. Соотношение неопределенности и принцип дополнительности
- •10. Волновое уравнение Шредингера
- •11. Стационарные состояния
- •Заключение
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Заключение
В данном учебном пособии изложены основные понятия, которыми оперирует квантовая физика – волновая функция оператор и прочие. При этом совершенно не затрагиваются вопросы исторического развития квантовых представлений. Пособие может служить введением к изучению квантовой электродинамике, теории твердого тела. Перечень литературы в библиографическом списке приведен в основном с целью указания места, где читатель может найти более подробное изложение вопросов, затронутых в учебном пособии.
Задачи
Вычислить коммутатор операторов: а)
 ,
б)
,
б)
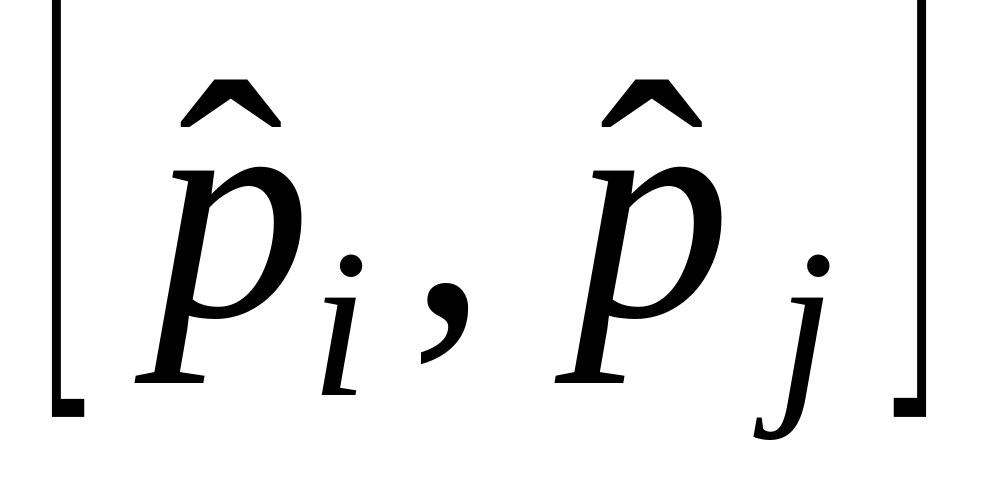 ,
в)
,
в)
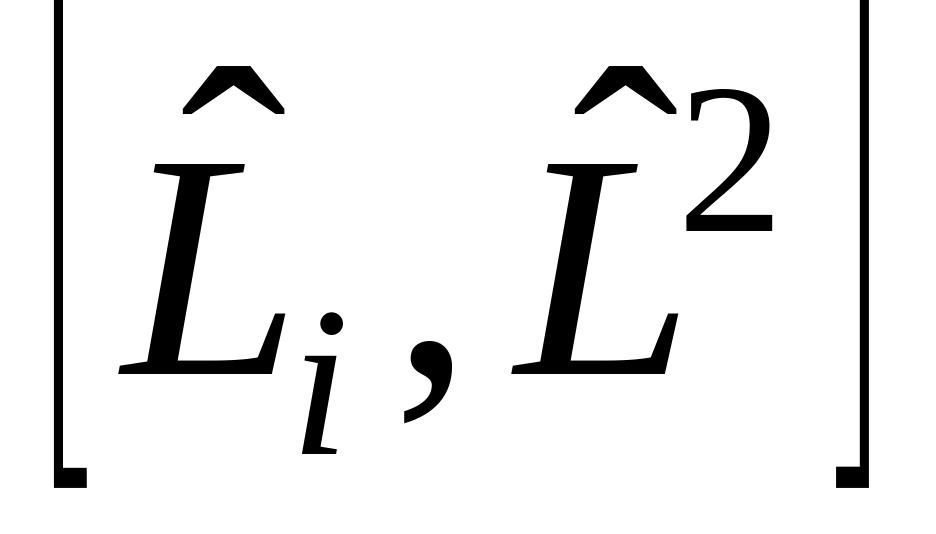 ,
г)
,
г)
 ,
д)
,
д)
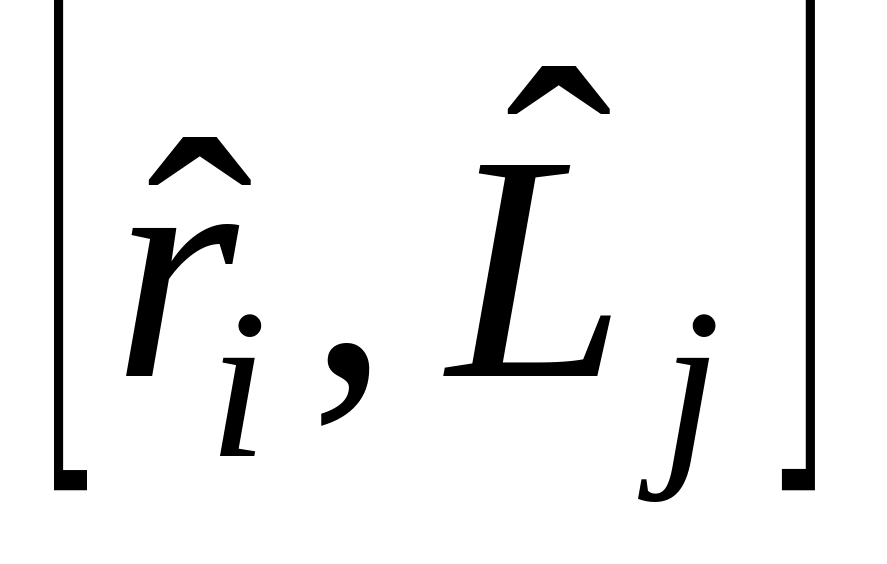 ,
е)
,
е)
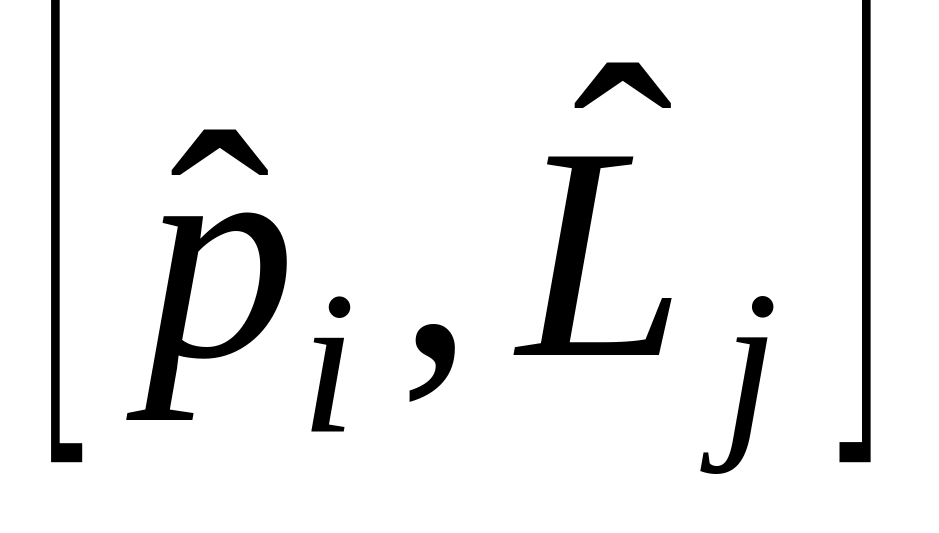 ,
ж)
,
ж)
 ,
з)
,
з)
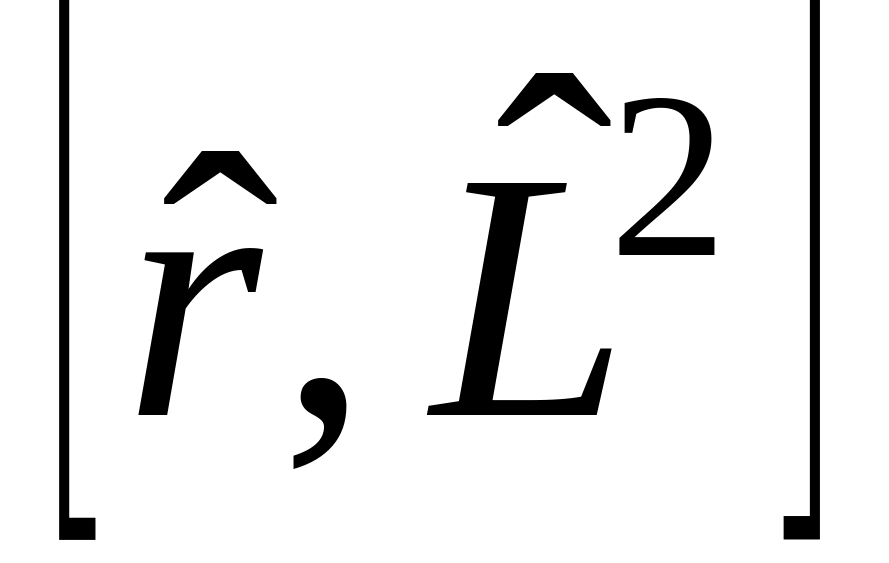 ,
и)
,
и)
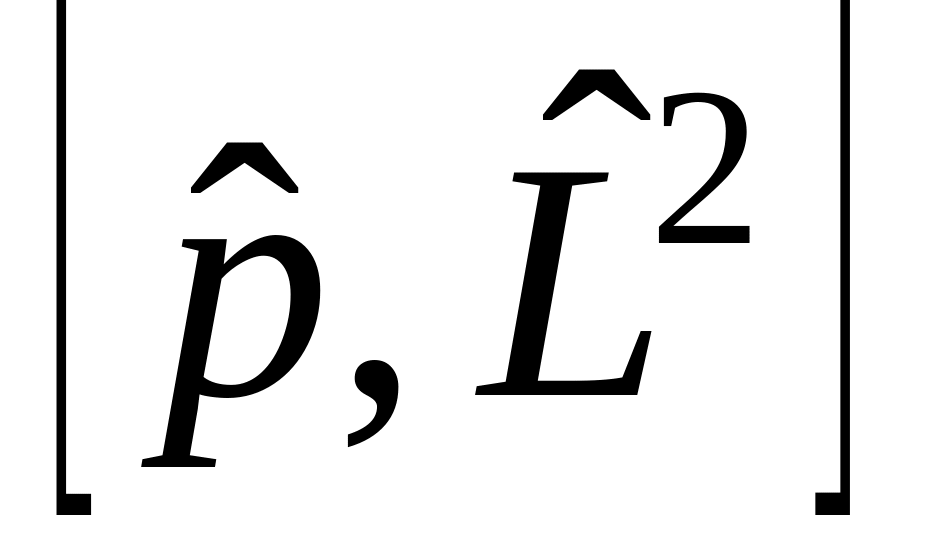 ,
к)
,
к)
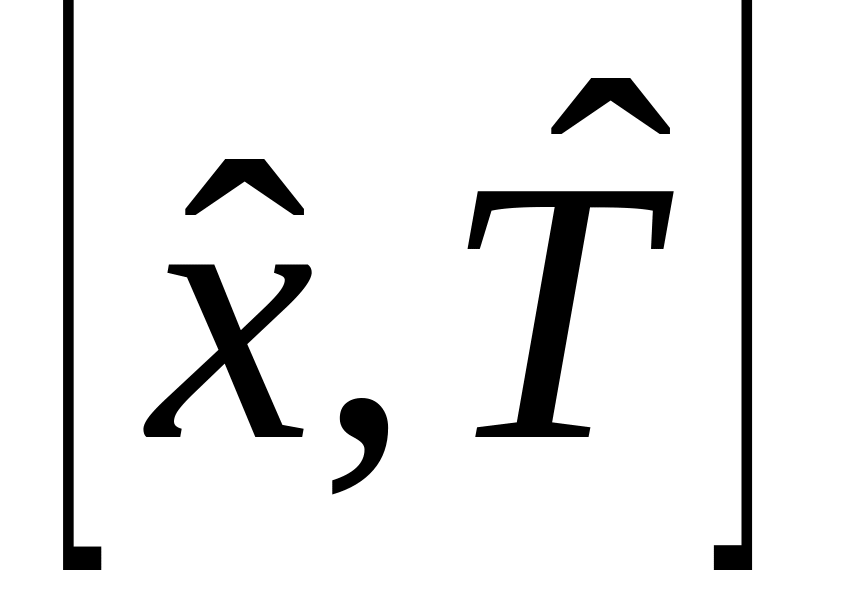 ,
л)
,
л)
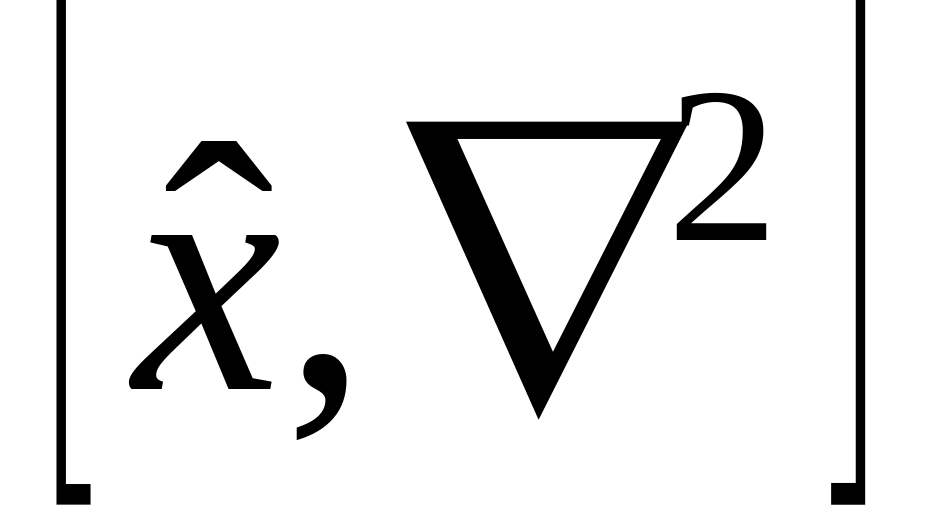 ,
м)
,
м)
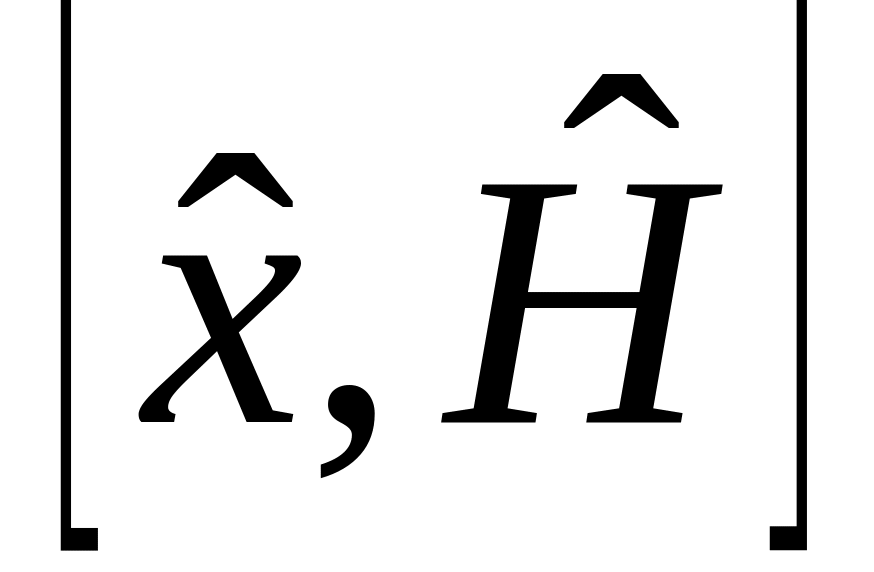 ,
н)
,
н)
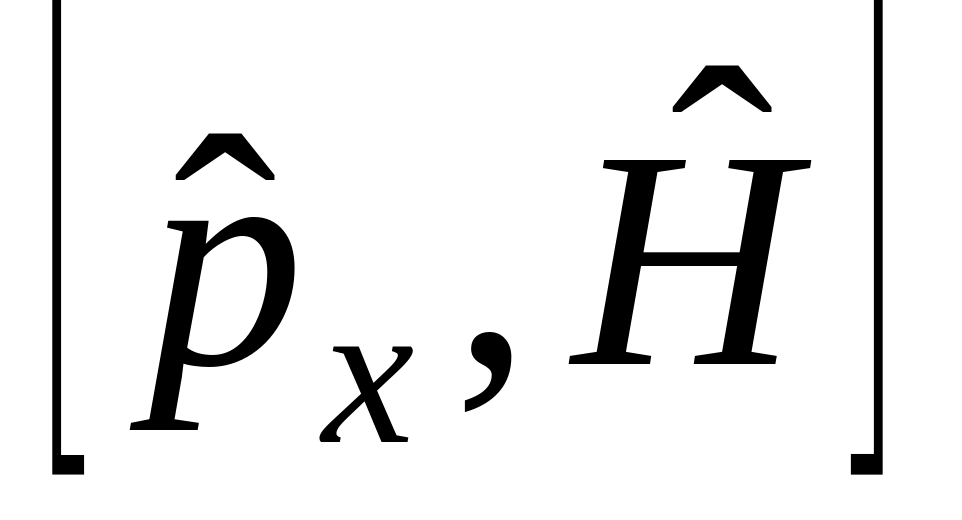 ,
о)
,
о)
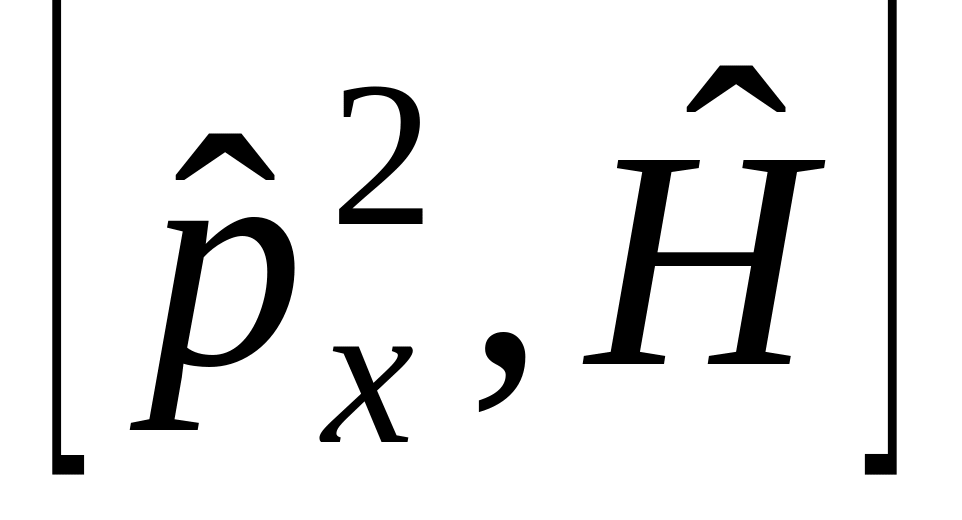 ,
п)
,
п)
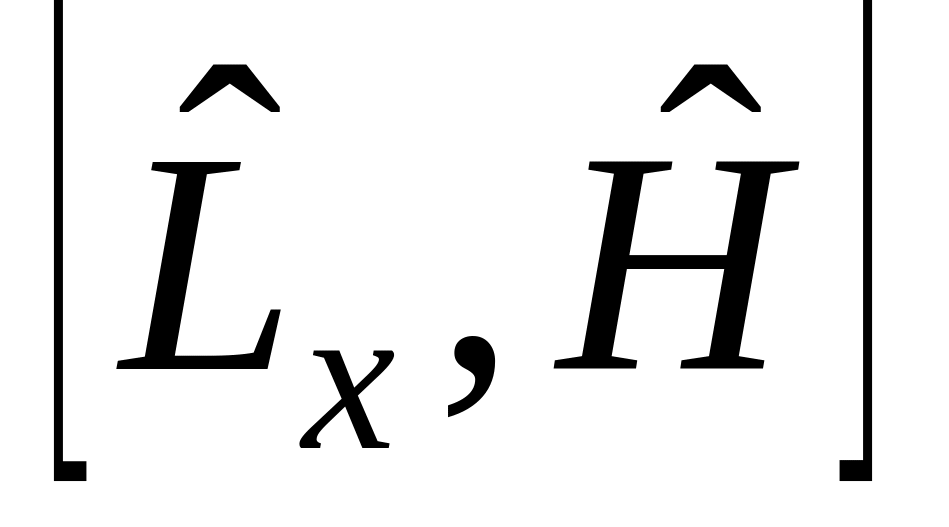 .
.Рассмотреть оператор. Является ли он линейным? Найти вид операторов, которые по отношению к нему, эрмитовы, обратные. А) Оператор изменения масштаба
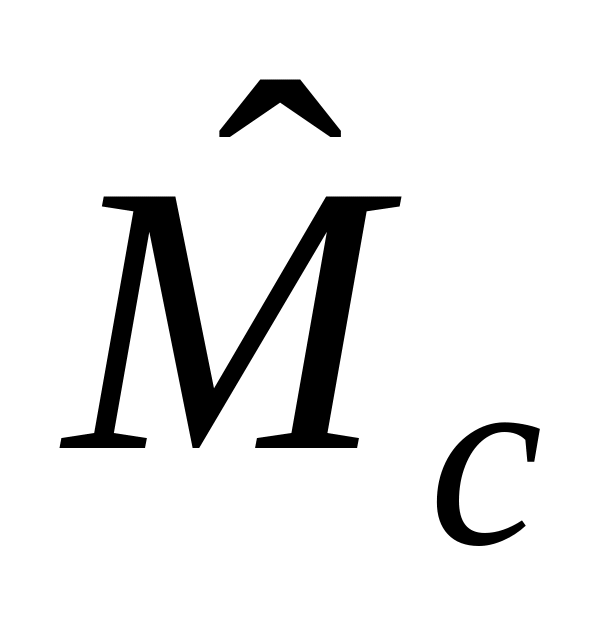 :
:
 ,
,
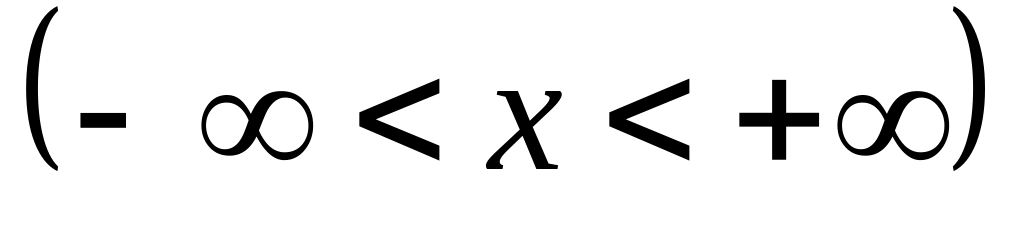 .
Б) Оператор отражения
.
Б) Оператор отражения
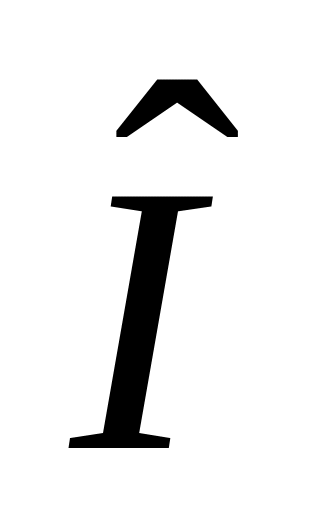 :
:
 ,
.
В) Оператор сдвига
,
.
В) Оператор сдвига
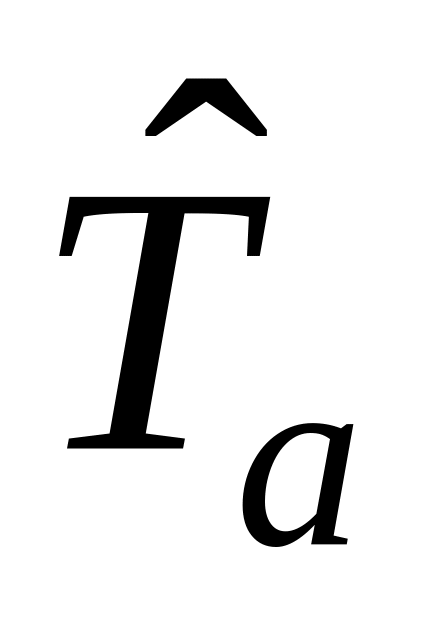 :
:
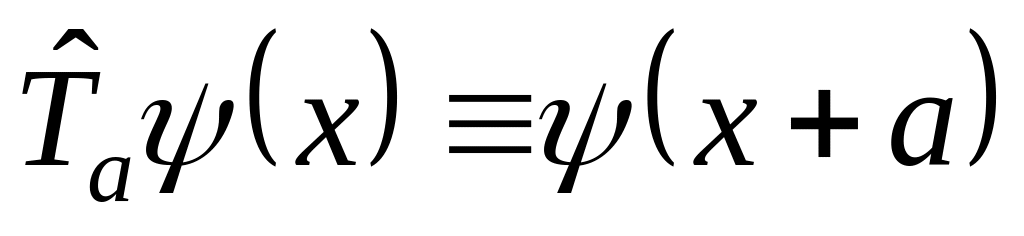 ,
.
Г) Оператор комплексного сопряжения
:
,
.
Г) Оператор комплексного сопряжения
:
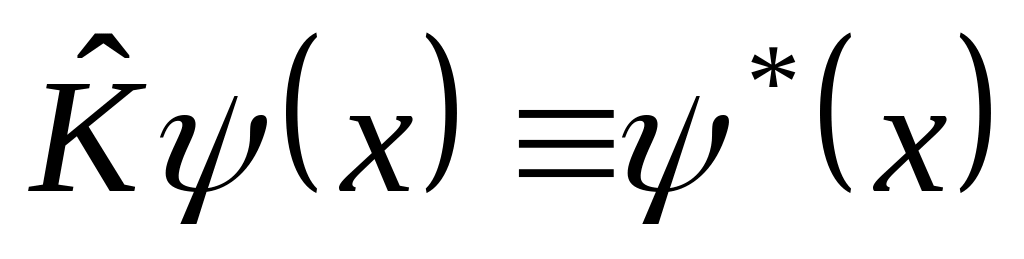 ,
.
Д) Оператор перестановки координат
двух частиц
,
.
Д) Оператор перестановки координат
двух частиц
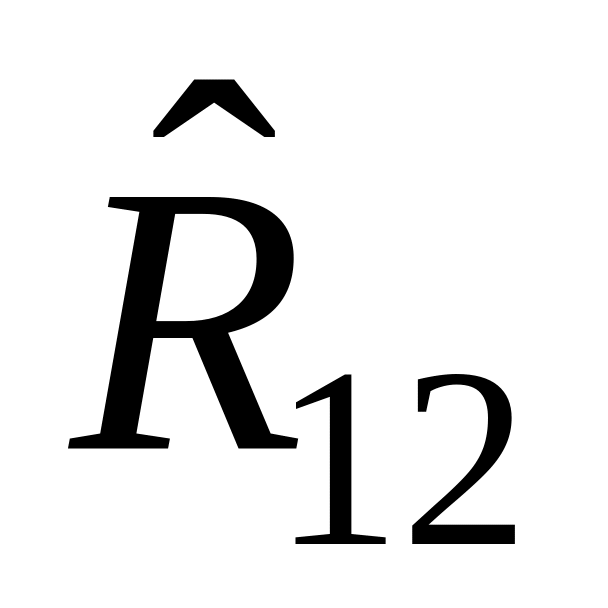 :
:
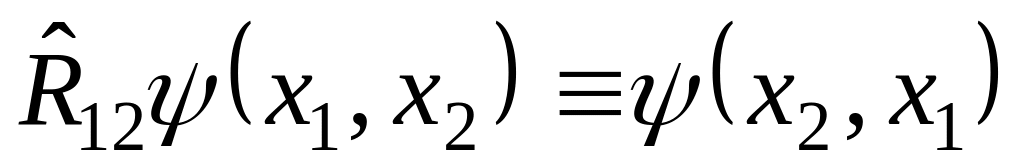 ,
.
,
.Выразить коммутаторы
 и
и
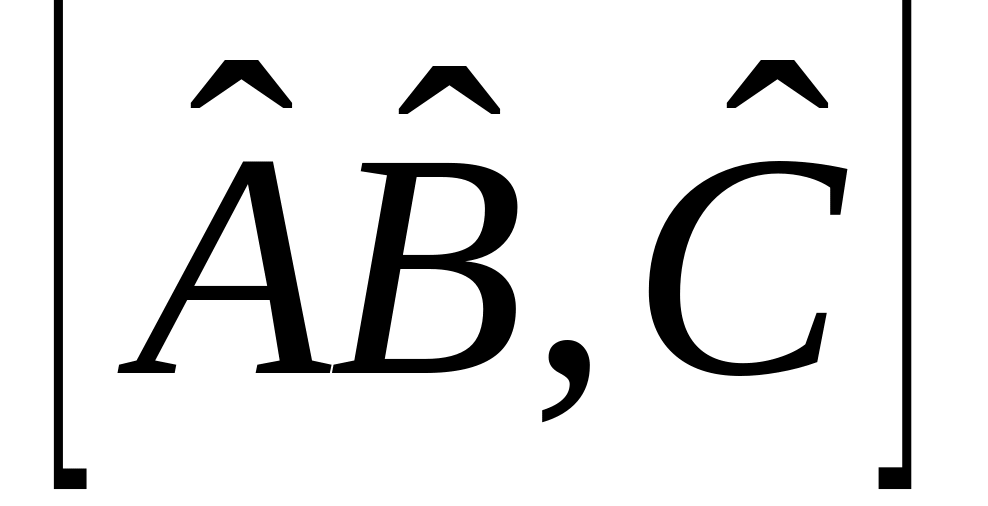 через
через
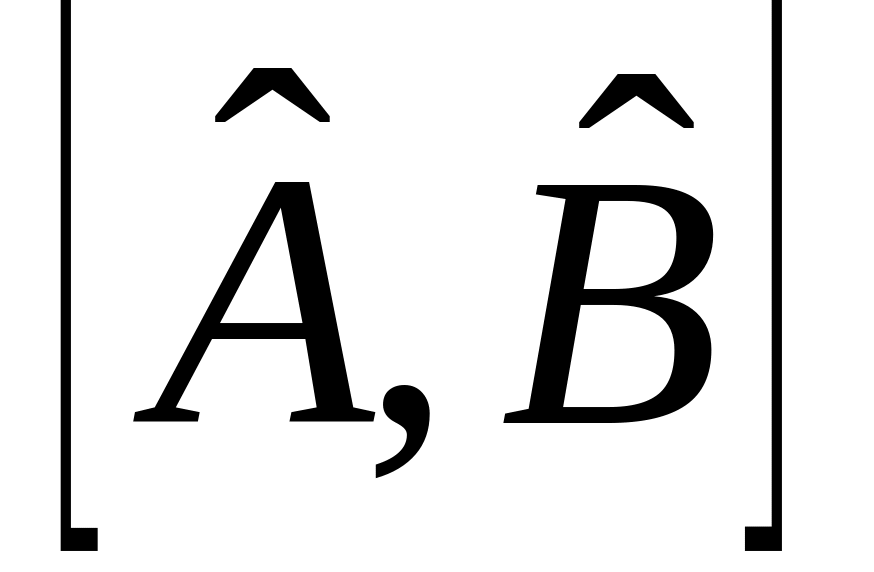 ,
,
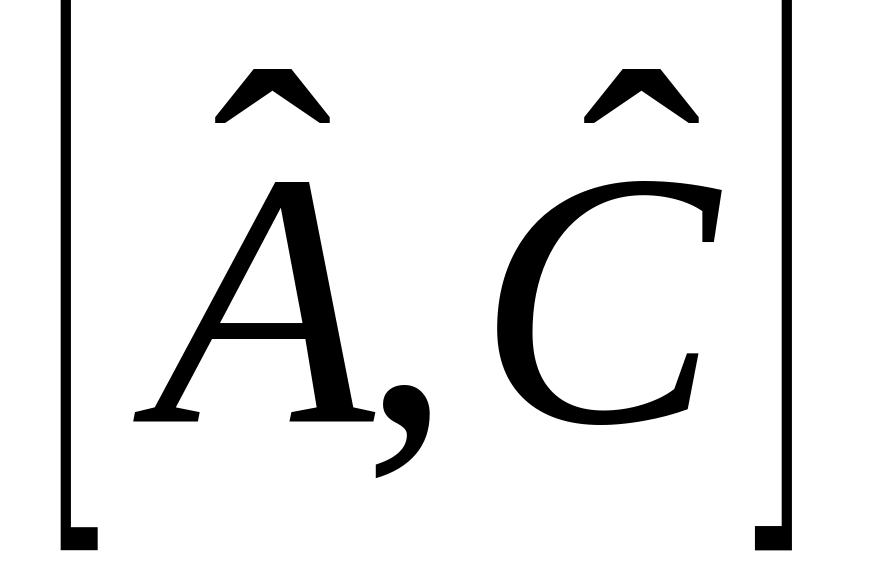 и
и
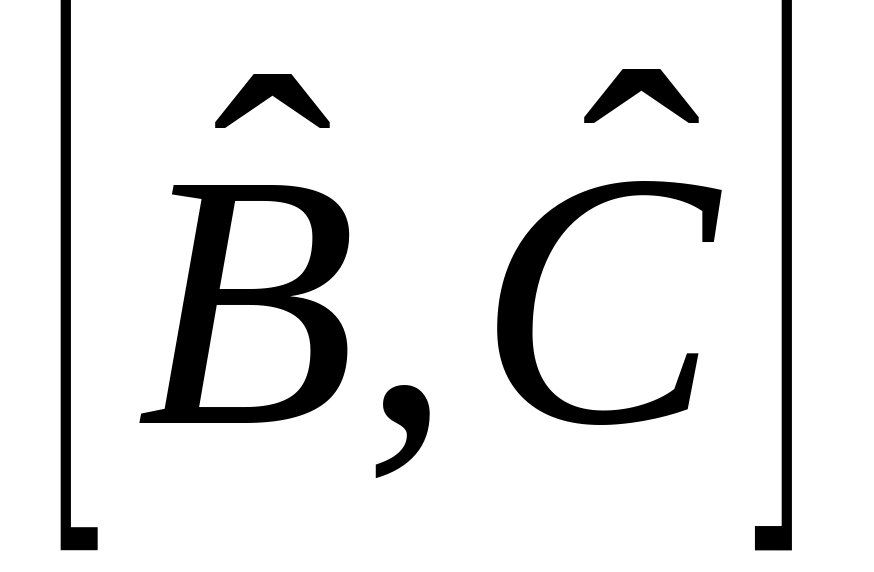 .
.Доказать, что если операторы
 и
и
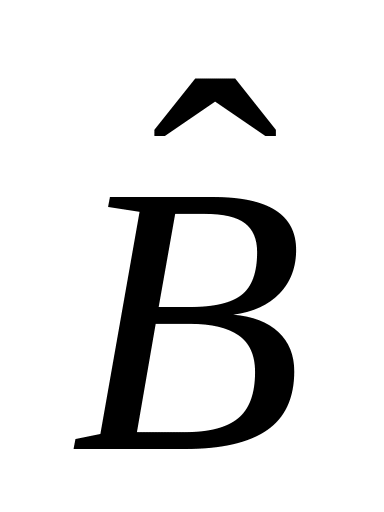 – эрмитовы, то эрмитовы и операторы:
а)
– эрмитовы, то эрмитовы и операторы:
а)
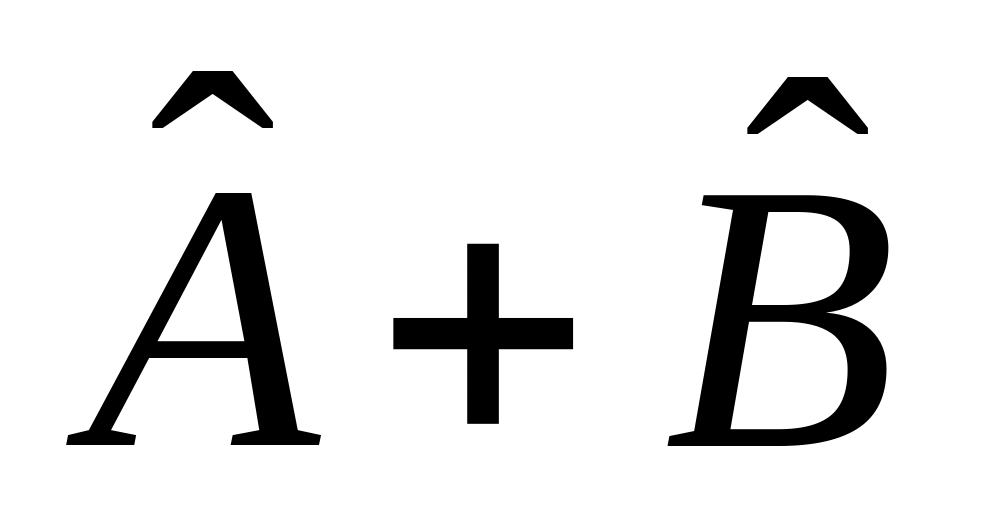 ,
б)
,
б)
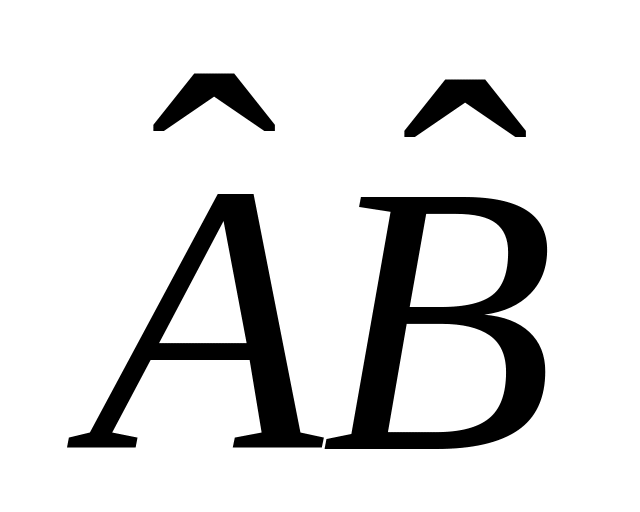 .
.Операторы
 и
и
 – эрмитовы,
– эрмитовы,
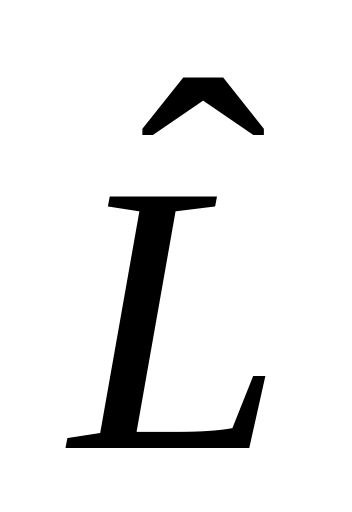 – произвольный оператор. Показать
эрмитовость оператора: а)
– произвольный оператор. Показать
эрмитовость оператора: а)
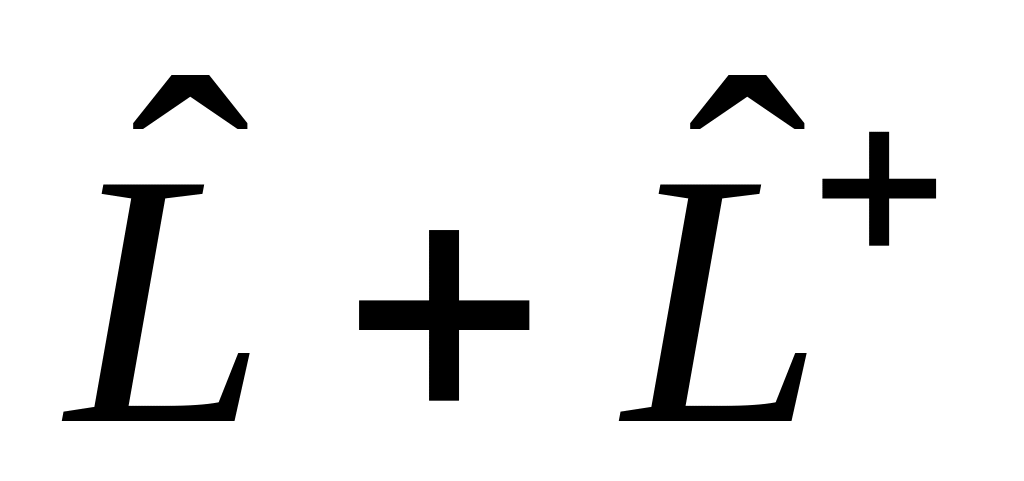 ,
б)
,
б)
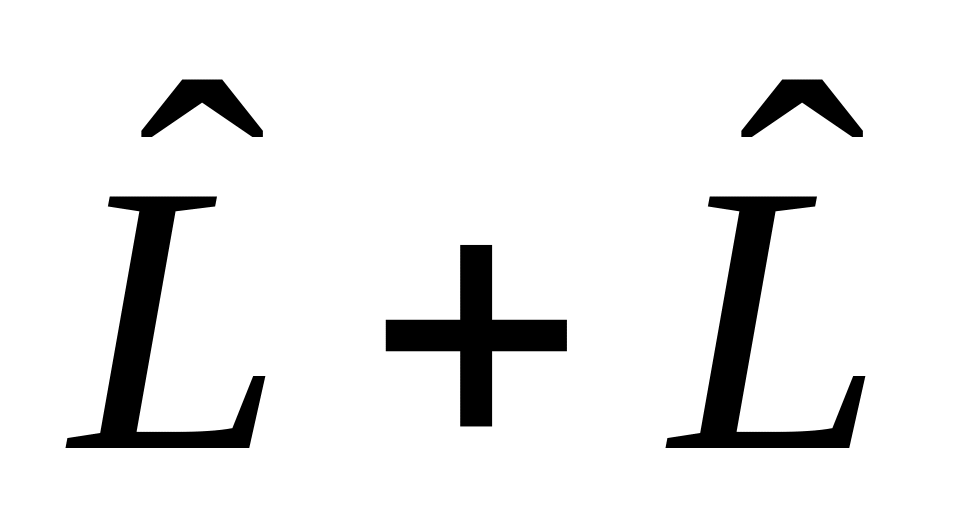 ,
в)
,
в)
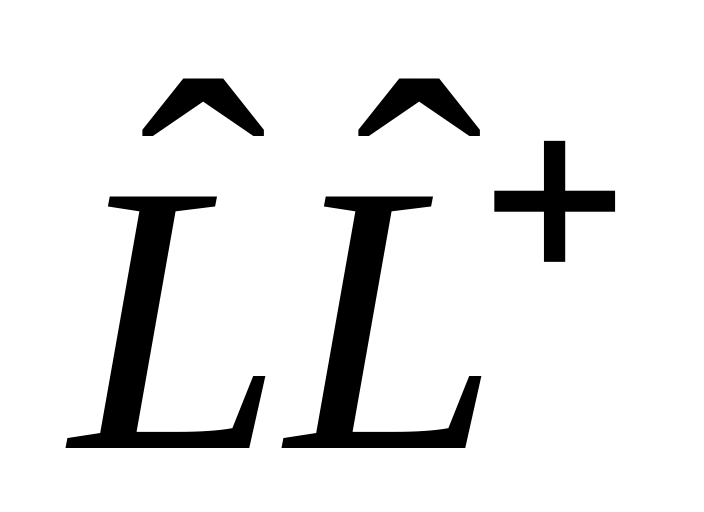 ,
г)
,
г)
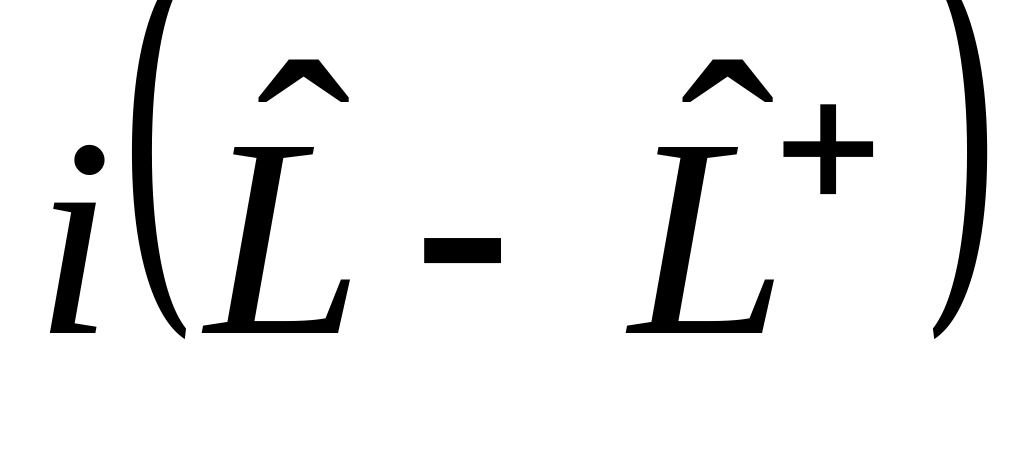 ,
д)
,
д)
 ,
е)
,
е)
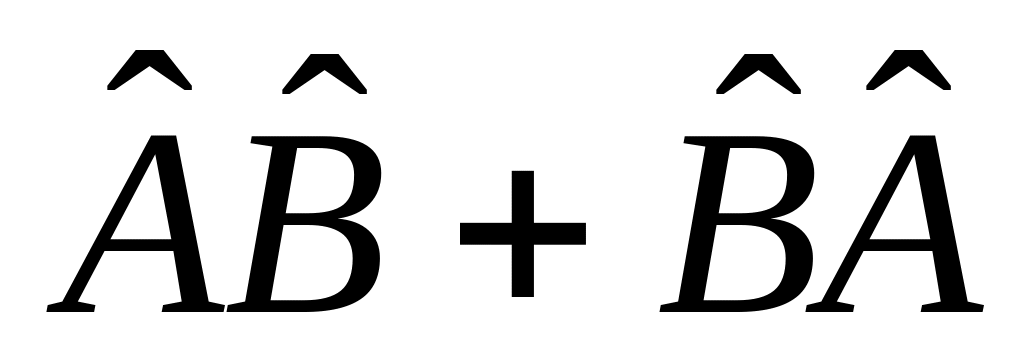 ,
ж)
,
ж)
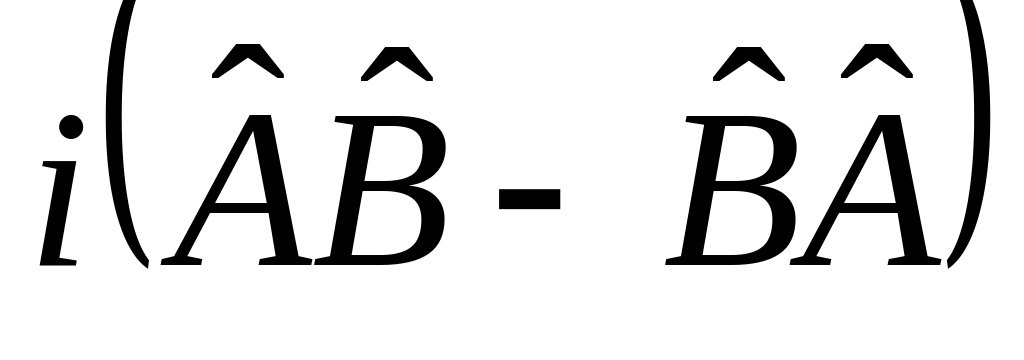 ,
з)
,
з)
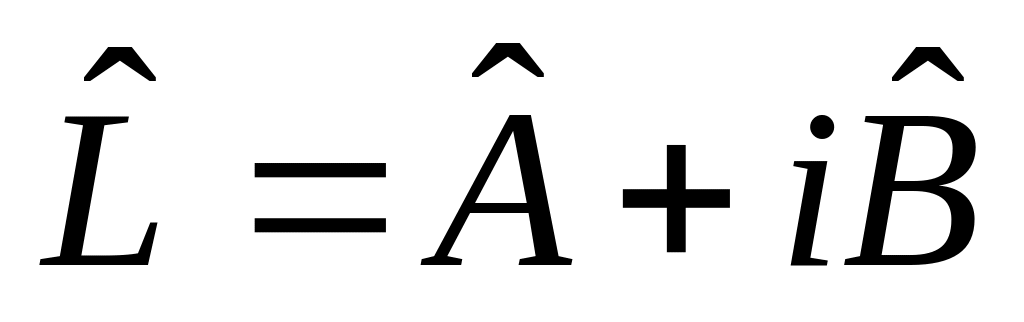 .
.Найти собственные функции и собственные значения. А) Физической величины, являющейся линейной комбинацией одноименных компонент импульса и координаты частицы
 .
Б) Оператора проекции момента количества
движения на ось
(
.
Б) Оператора проекции момента количества
движения на ось
( ).
В) Оператора координаты
).
В) Оператора координаты
 .
Г) Оператора проекции импульса
.
Г) Оператора проекции импульса
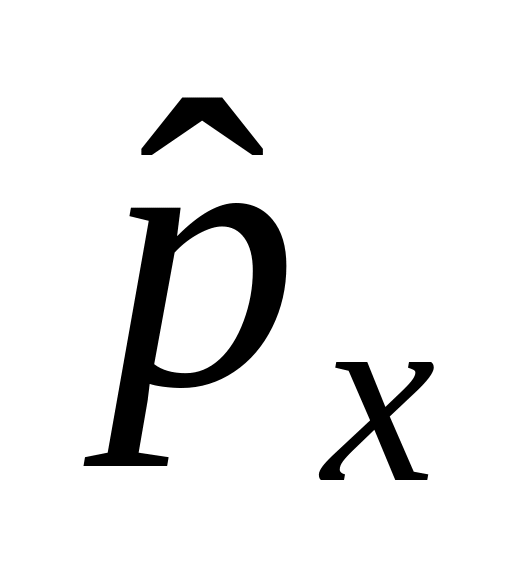 .
Д) Оператора
.
Д) Оператора
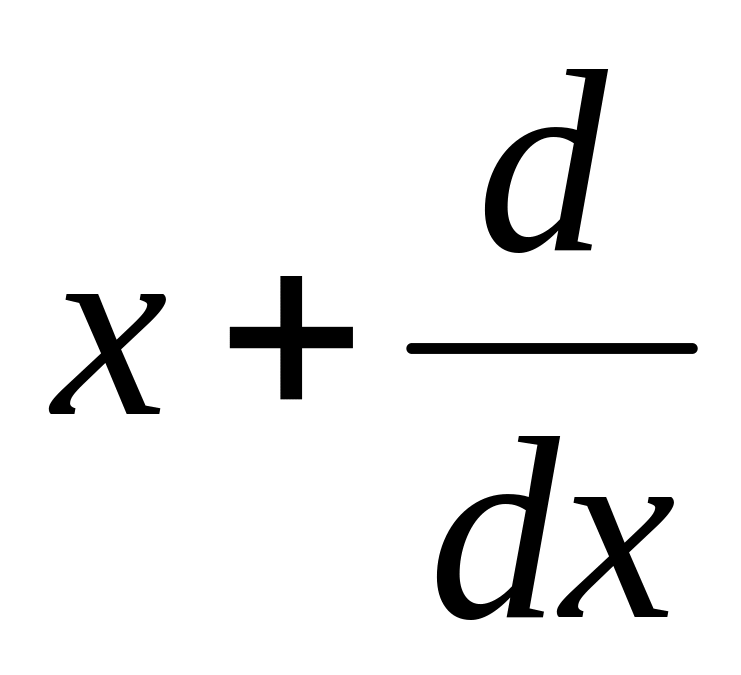 .
Е) Оператора
.
Е) Оператора
 .
Ж) Оператора
.
З) Оператора
.
Ж) Оператора
.
З) Оператора
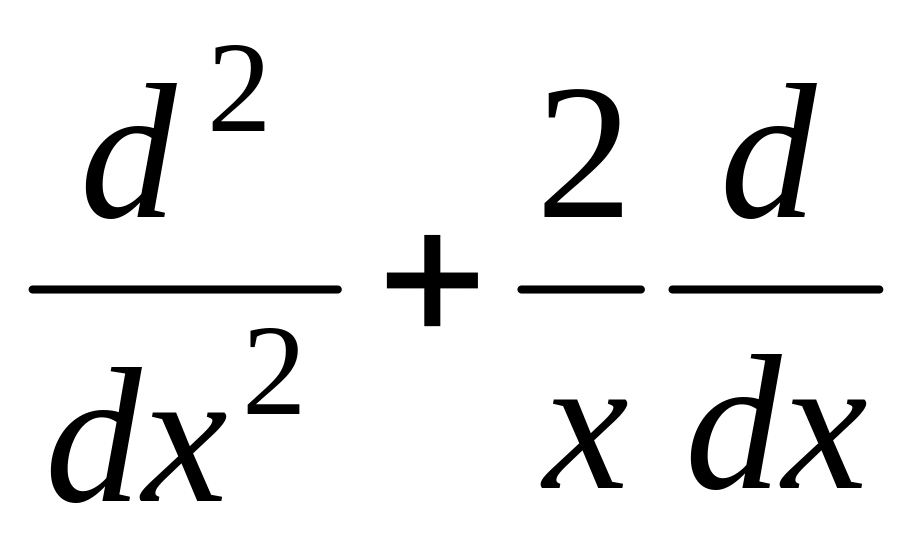 .
И) Оператора
.
И) Оператора
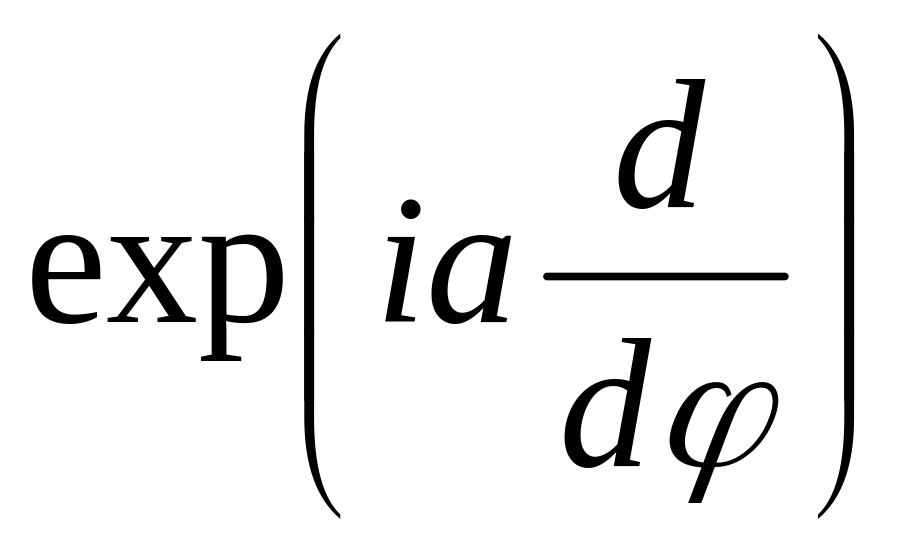 .
.Доказать, что функция
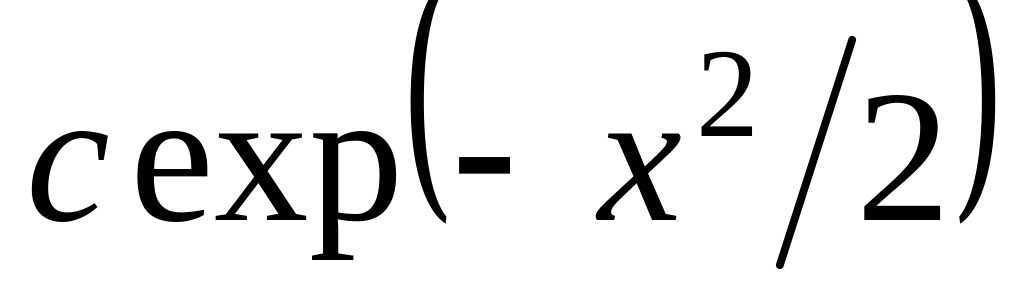 является собственной функцией оператора
является собственной функцией оператора
 и найти соответствующее собственное
значение.
и найти соответствующее собственное
значение.Найти связь между средними значениями координаты и импульса частицы в двух состояниях, волновые функции
 и
и
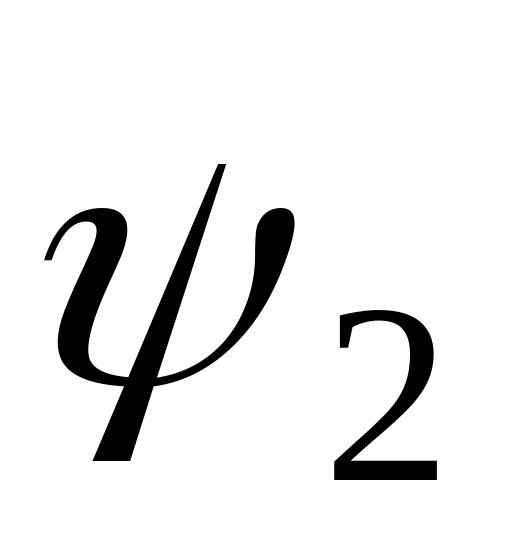 которых связаны соотношением: а)
которых связаны соотношением: а)
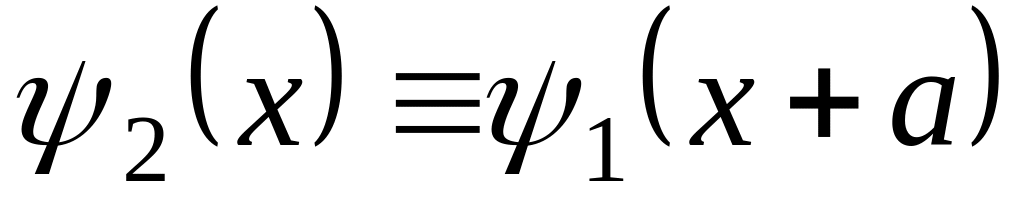 ,
б)
,
б)
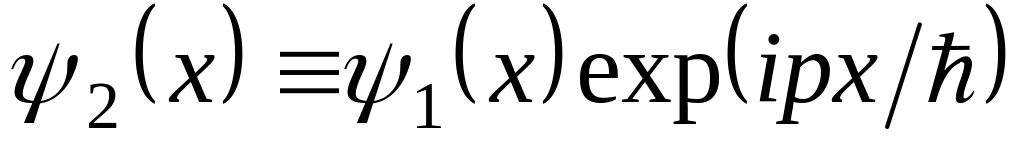 .
.Доказать, что справедливо соотношение неопределенности:
![]() .
.
Доказать, что справедливо соотношение неопределенности:
![]() .
.
Для частицы, состояние которой задано функцией
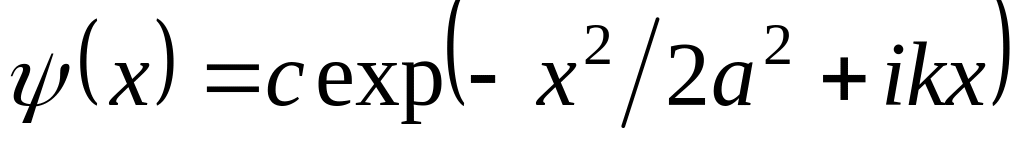 ,
проверить соотношение неопределенности
для координаты и импульса.
,
проверить соотношение неопределенности
для координаты и импульса.Коммутатор операторов и имеет вид
 ,
где
,
где
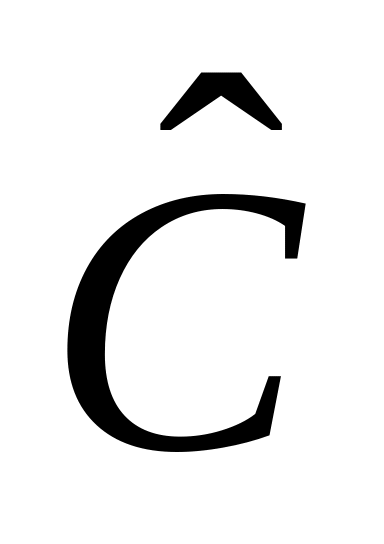 – эрмитов оператор. Доказать, что
справедливо соотношение неопределенности:
– эрмитов оператор. Доказать, что
справедливо соотношение неопределенности:
![]() .
.
Вычислив среднее значение энергии
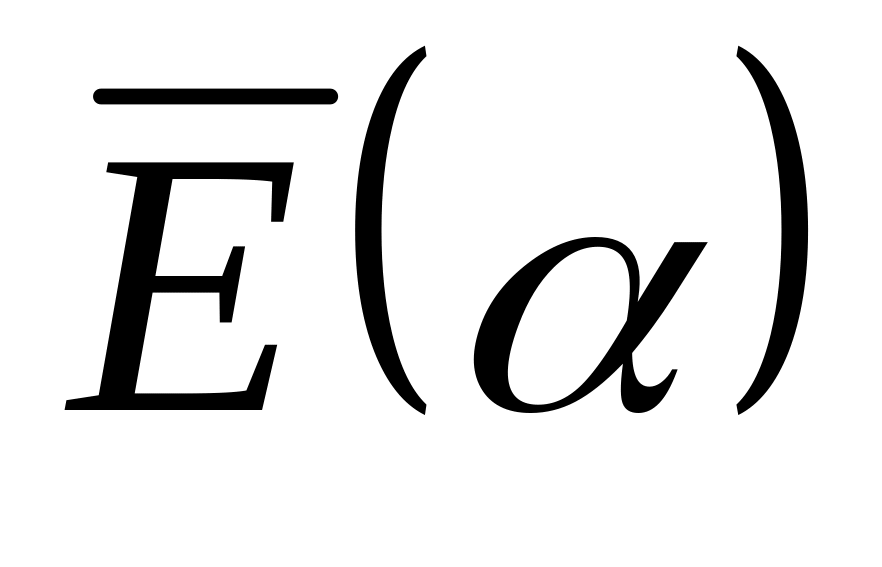 в состоянии с волновой функцией
в состоянии с волновой функцией
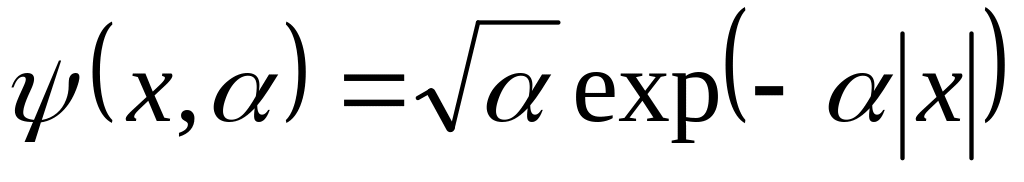 ,
,
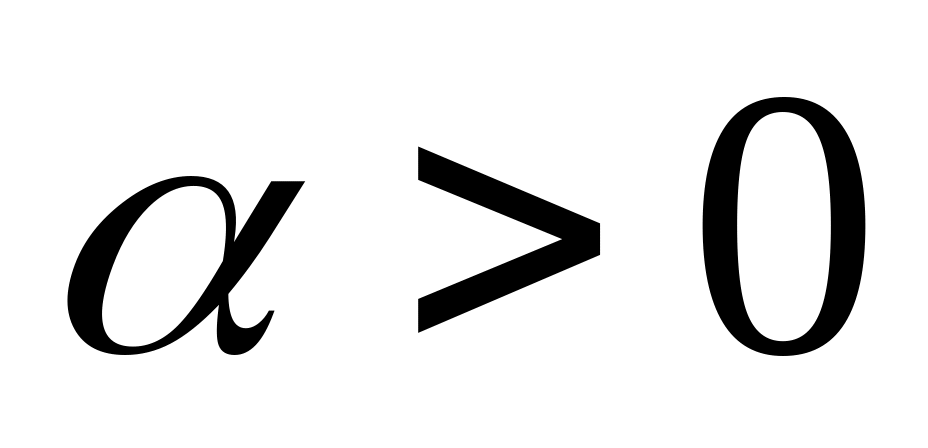 ,
показать, что в любом одномерном
потенциале
,
показать, что в любом одномерном
потенциале
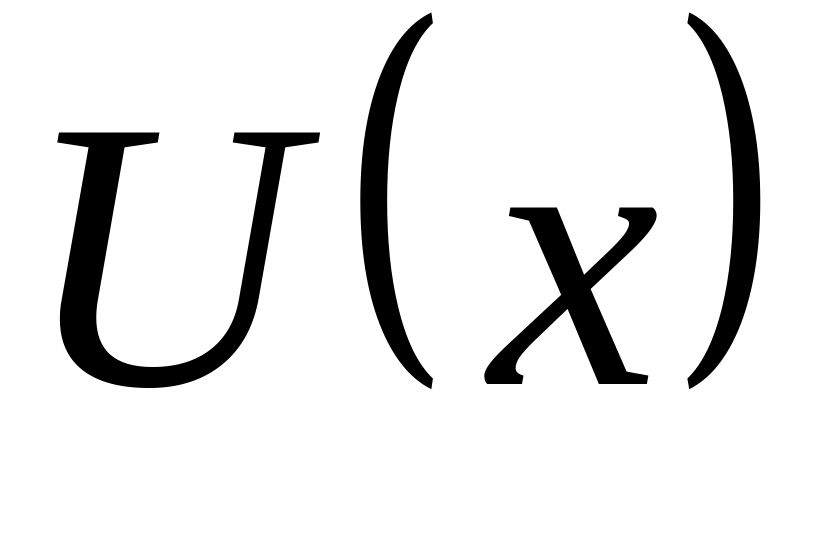 ,
удовлетворяющем условиям
,
удовлетворяющем условиям
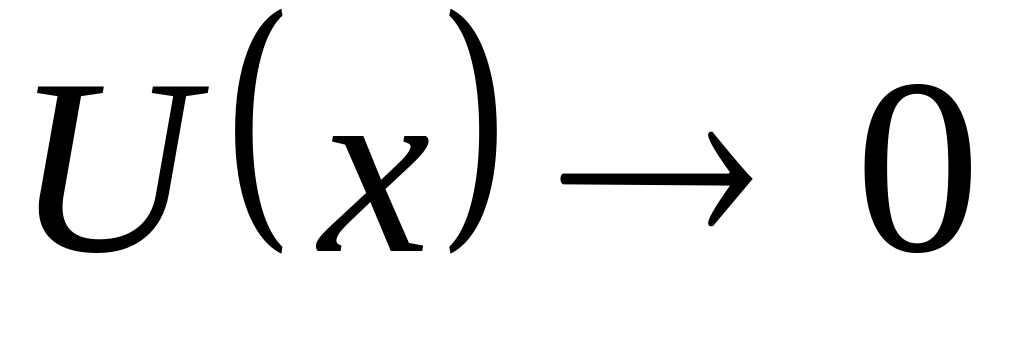 при
при
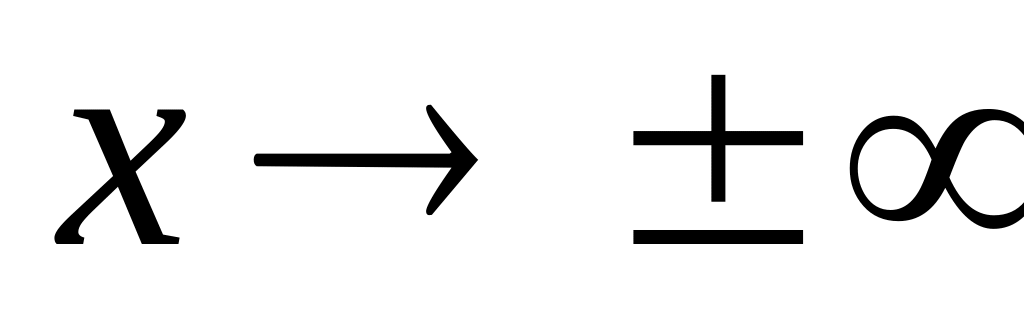 и
и
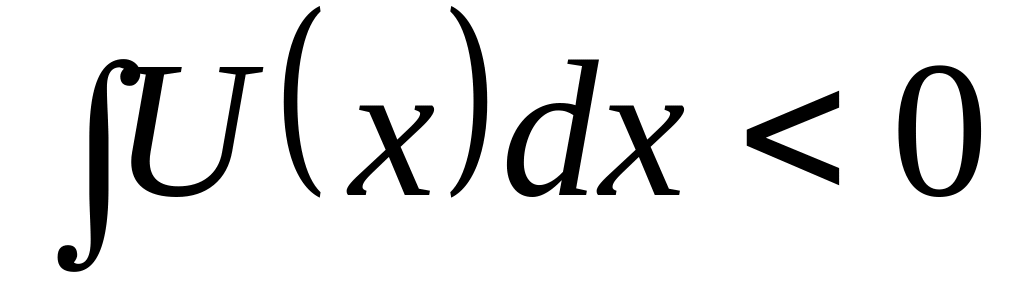 ,
всегда есть хотя бы одно состояние
дискретного спектра с энергией
,
всегда есть хотя бы одно состояние
дискретного спектра с энергией
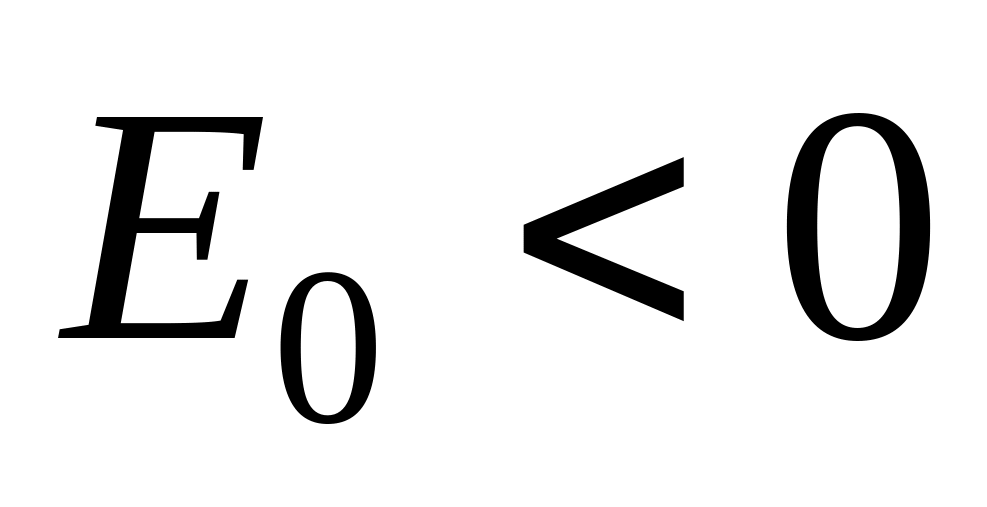 .
.
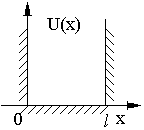
Решить стационарное уравнение Шредингера для частицы массы
 ,
движущейся в одномерной потенциальной
яме с бесконечно высокими стенками
(рис. 2).
,
движущейся в одномерной потенциальной
яме с бесконечно высокими стенками
(рис. 2).
Рис. 2.
Ч
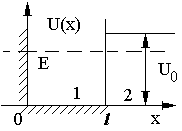
Рис. 3.
астица массы находится в однородном потенциальном поле , где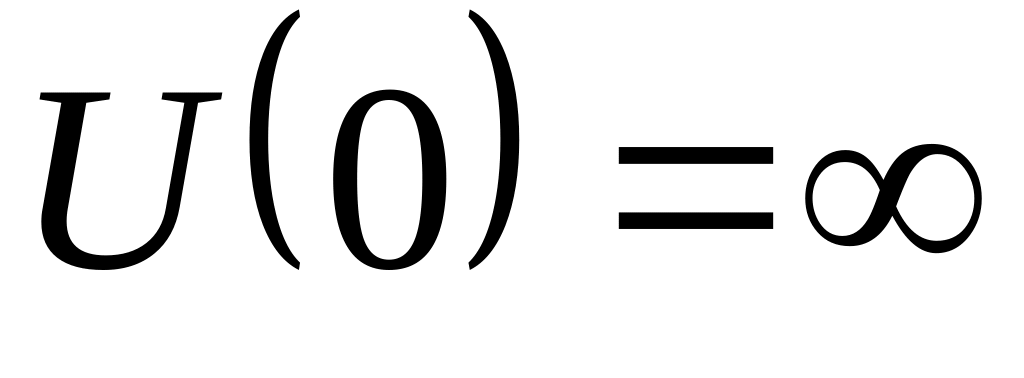 (рис. 3). Найти возможные уровни энергии
частицы в области
(рис. 3). Найти возможные уровни энергии
частицы в области
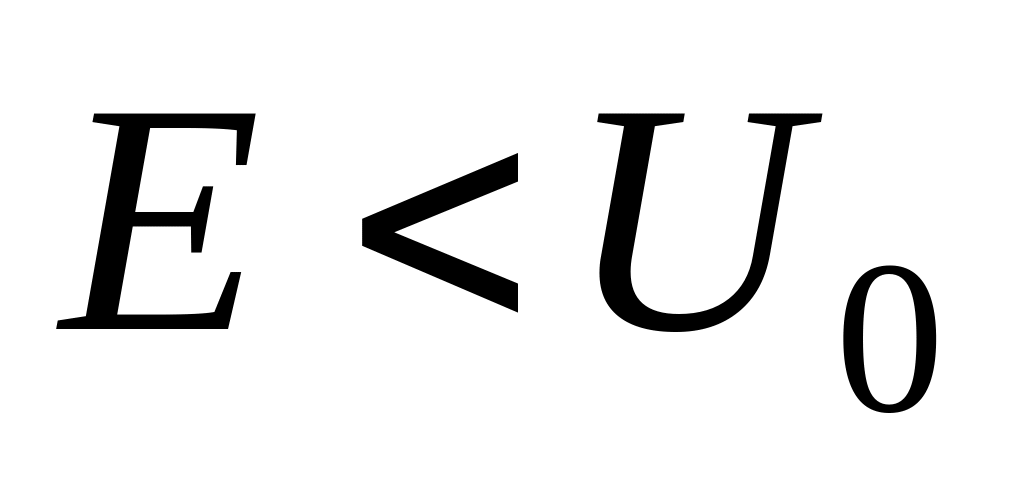 .
.
Ч
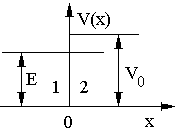
Рис. 4.
астица, двигаясь в положительном направлении оси , падает на потенциальный порог (рис. 4). Рассмотрев случай
(рис. 4). Рассмотрев случай
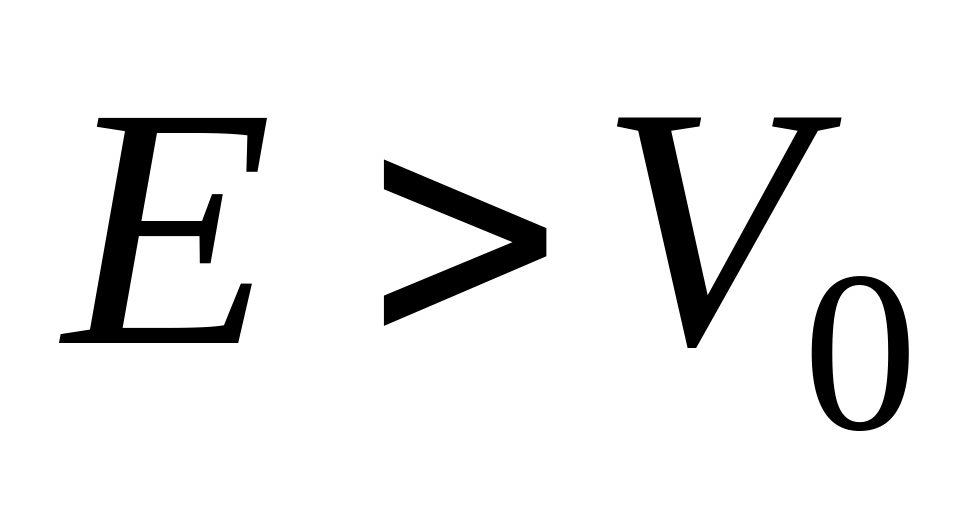 и
и
 ,
найти коэффициенты прохождения и
отражения частиц.
,
найти коэффициенты прохождения и
отражения частиц.
Потенциал имеет вид
 ,
где
,
где
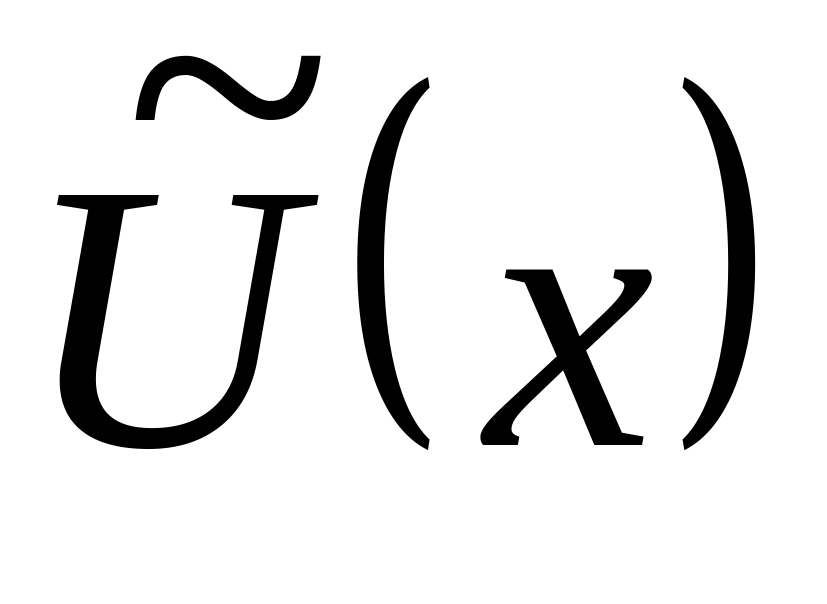 – ограниченная функция. Как ведут себя
решение уравнения Шредингера и его
производная в точке
– ограниченная функция. Как ведут себя
решение уравнения Шредингера и его
производная в точке
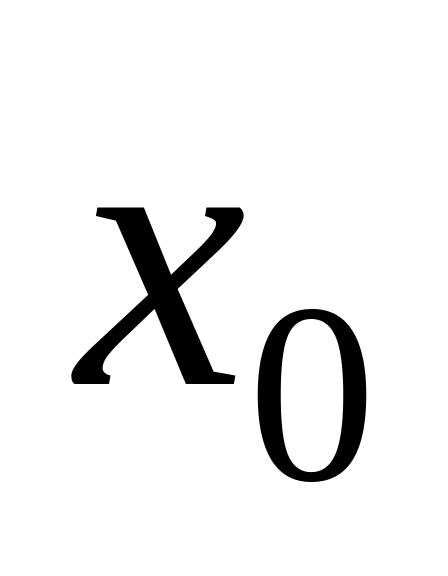 ?
?
Для частицы найти число связанных состояний в зависимости от значений параметров потенциала :
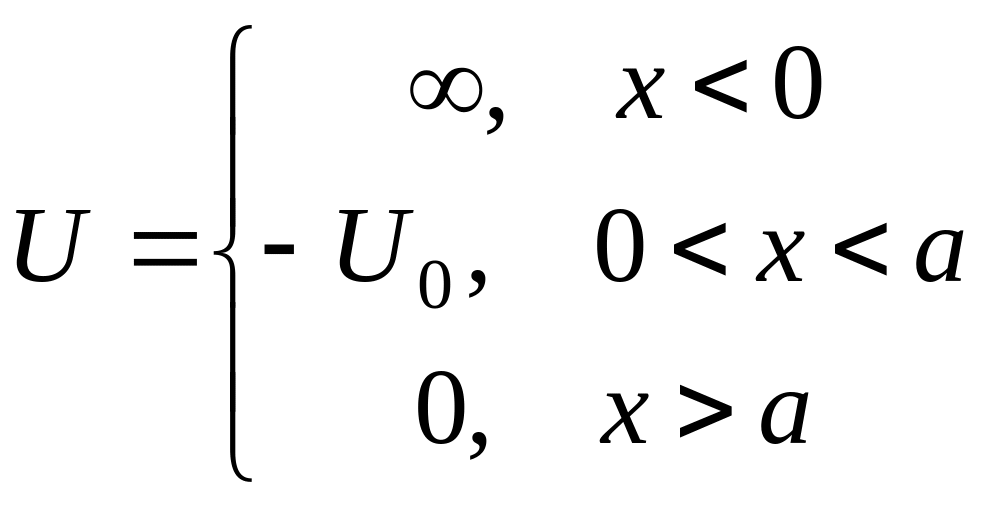 (рис.5).
(рис.5).
Рис. 5.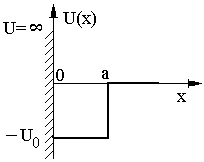
Ч
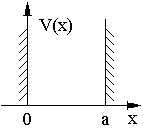 астица
массы
находится в бесконечно глубокой
потенциальной яме ширины
астица
массы
находится в бесконечно глубокой
потенциальной яме ширины
 (рис. 6). Найти энергии стационарных
состояний частицы и соответствующие
им волновые функции.
(рис. 6). Найти энергии стационарных
состояний частицы и соответствующие
им волновые функции.
Рис. 6.
Д

Рис. 7.
ля частицы найти число связанных состояний в зависимости от значений параметров потенциала :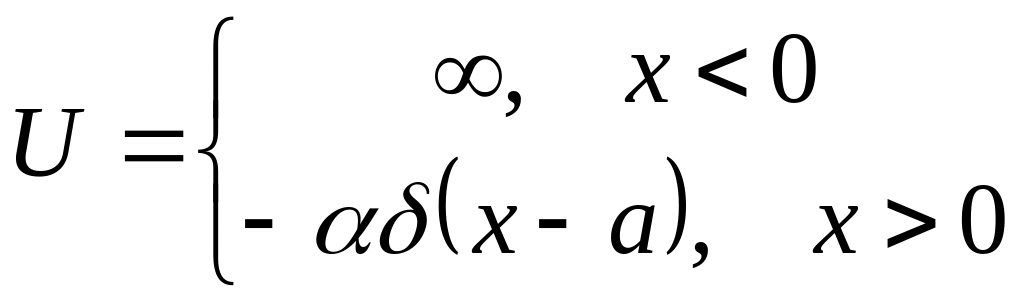 (рис. 7).
(рис. 7).
Н
 айти
энергетические уровни и нормированные
волновые функции состояний дискретного
спектра частицы в
айти
энергетические уровни и нормированные
волновые функции состояний дискретного
спектра частицы в
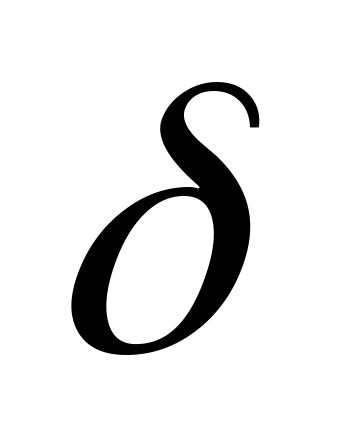 -потенциале
-потенциале
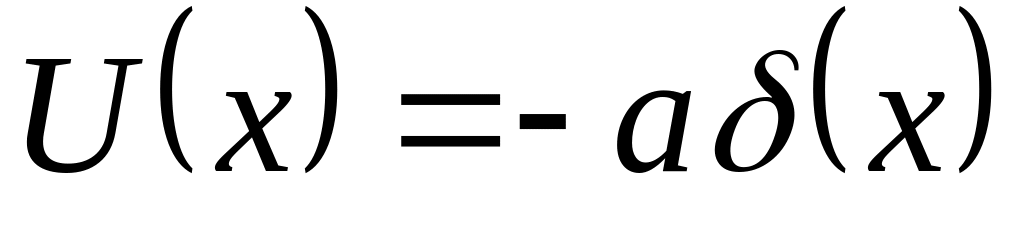 (рис. 8).
(рис. 8).
Н
Рис. 8.
айти энергетические уровни и волновые функции состояний дискретного спектра частицы в потенциале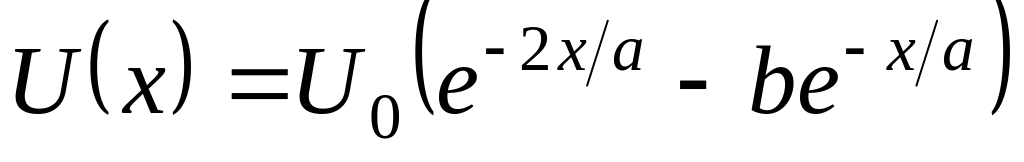 ,
,
 ,
,
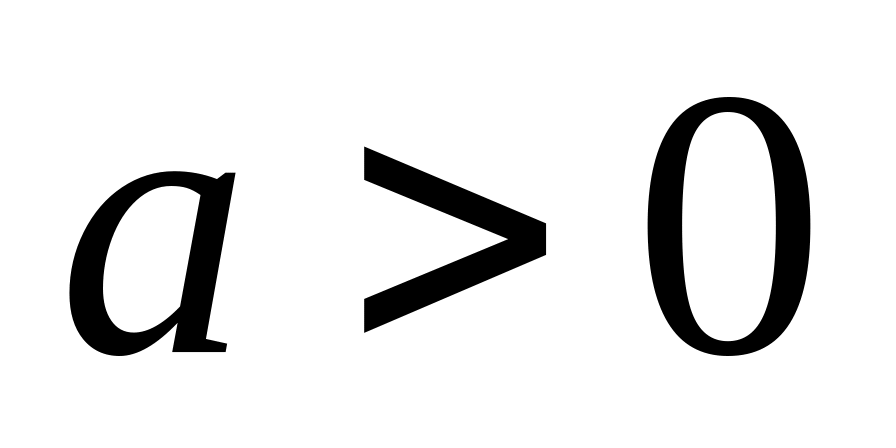 ,
,
 .
.
Н
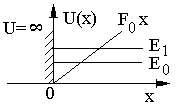 айти
энергетический спектр и волновые
функции стационарных состояний частицы
в потенциале, изображенном на рис. 9.
айти
энергетический спектр и волновые
функции стационарных состояний частицы
в потенциале, изображенном на рис. 9.
Рис. 9.
Найти энергетические уровни и волновые функции состояний дискретного спектра частицы в потенциале
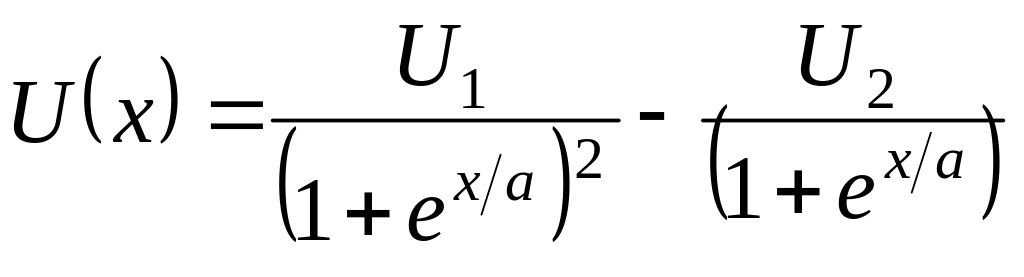 ,
,
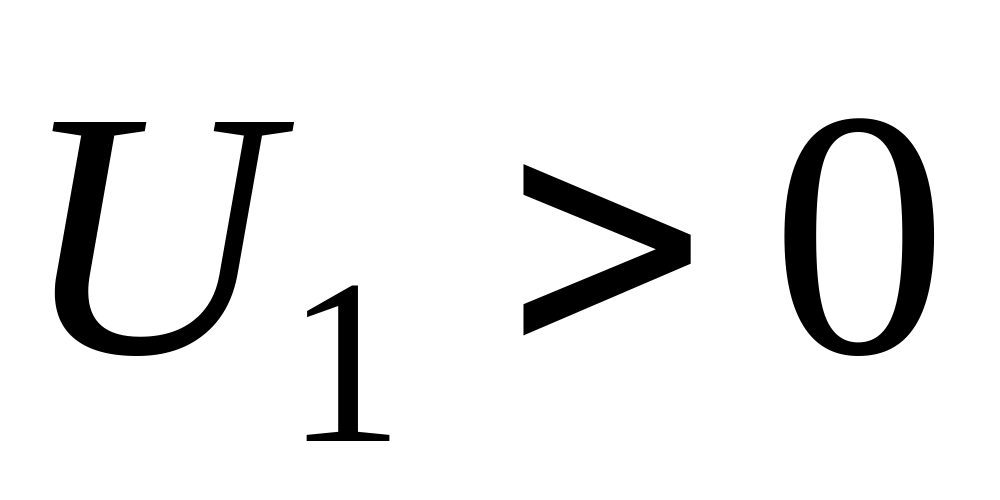 ,
,
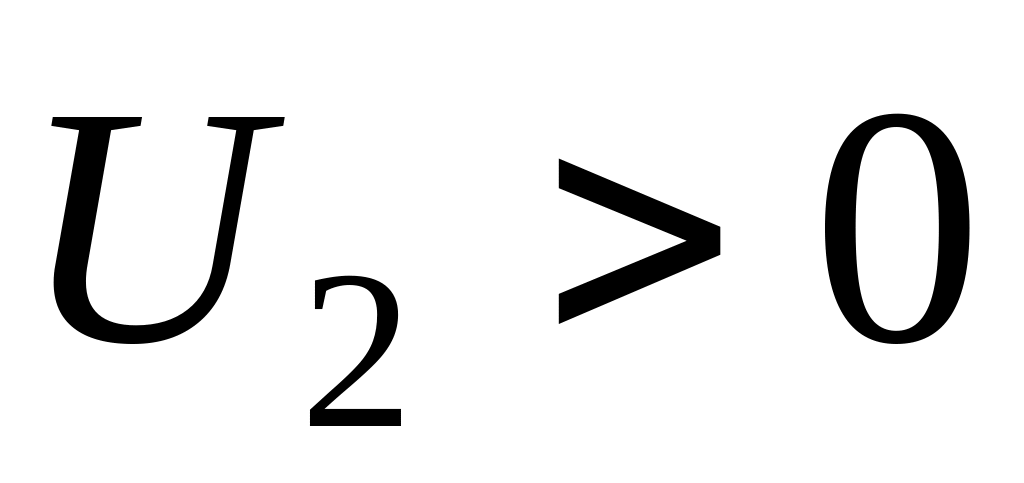 ,
.
,
.
Н
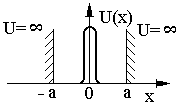
Рис. 10.
айти энергетический спектр и волновые функции частицы в потенциале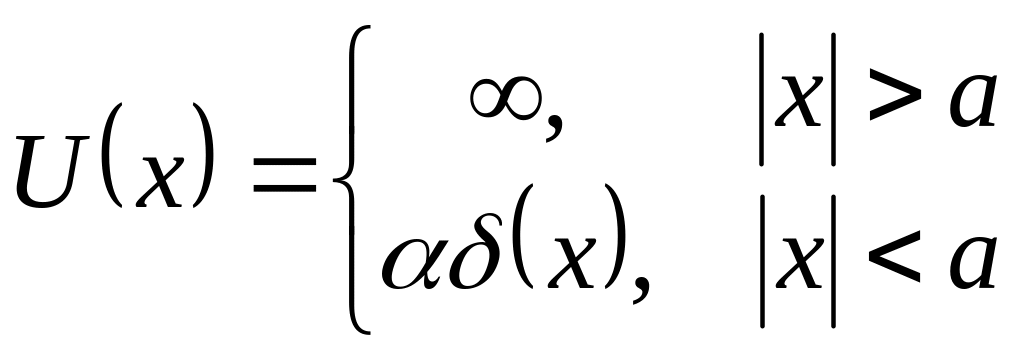 ,
.
,
.
