
- •Введение
- •Варианты контрольных работ
- •1. Контрольная работа №3 Электромагнетизм. Колебания
- •1.1 Законы и формулы
- •1.2 Примеры решения и оформления задач
- •1.3 Задачи к контрольной работе №3
- •Физические величины
- •2. Контрольная работа №4 Волновая оптика. Квантовая природа излучения. Элементы атомной и ядерной физики
- •2.1 Законы и формулы
- •Волновая оптика
- •Квантовая природа излучения. Элементы квантовой механики и ядерной физики
- •2.2 Примеры решения задач
- •2.3 Задачи к контрольной работе №4
- •Массы изотопов некоторых элементов
- •Оглавление
- •394006 Воронеж, ул. 20-летия Октября, 84
2.2 Примеры решения задач
Задача
1. В просветленной оптике для устранения
отражения света на поверхность линзы
наносится тонкая пленка вещества с
показателем преломления ( = 1,26)
меньшим, чем у стекла. При какой наименьшей
толщине пленки отражение света от линзы
не будет наблюдаться? Длина волны
падающего света 0,55 мкм, угол падения
300.
= 1,26)
меньшим, чем у стекла. При какой наименьшей
толщине пленки отражение света от линзы
не будет наблюдаться? Длина волны
падающего света 0,55 мкм, угол падения
300.
Дано: = 0,55 мкм = 5,5∙10-7 м
= 1,26 |
Рисунок 7 |
Найти:
|
|
|
Решение
Лучи 1 и 2 отражаются от среды с большим показателем преломления (см. рис. 7), поэтому как на верхней, так и на нижней поверхности пленки происходит потеря полуволны, и, следовательно, оптическая разность хода лучей равна
 .
.
Отражения света от линзы не будет, если выполнится условие минимума освещенности при интерференции лучей 1 и 2 (условие минимума интерференции света):
 или
или
 ,
,
где k = 0, 1, 2, … .
Толщина пленки будет минимальна при = 0. Отсюда
 .
.
Подставляя числовые данные, найдем минимальную толщину пленки
 м = 0,117 мкм.
м = 0,117 мкм.
Ответ: = 0,117 мкм.
Задача 2. На дифракционную решетку нормально падает монохроматический свет с длиной волны 0,65 мкм. На экране, расположенном параллельно решетке и отстоящем от нее на расстоянии 0,5 м, наблюдается дифракционная картина. Расстояние между дифракционными максимумами первого порядка равно 10 см. Определить постоянную дифракционной решетки и общее число максимумов, получаемых с помощью этой решетки.
Дано: = 0,65 мкм = 6,5∙10-7 м
= 0,1 м =1 |
Рисунок 8
|
Найти:
,
|
|
|
Решение
Картина распределения интенсивности света на экране при дифракции на решетке показана на рис. 8. Условие максимума интенсивности света на дифракционной решетке
, (1)
где – постоянная (период) решетки, – угол дифракции, – длина волны падающего света = 0, 1, 2, … – порядок максимума.
По
условию задачи
 ,
поэтому
,
поэтому
 . (2)
. (2)
Подставляя (2) в (1), получим
 или
или
 . (3)
. (3)
Вычислим постоянную решетки при = 1
 м = 6,5 мкм.
м = 6,5 мкм.
Для определения общего количества максимумов, получаемых с помощью дифракционной решетки, найдем максимальный порядок дифракции. Максимальный угол отклонения лучей от нормального направления распространения не может превышать 900, т.е. формула (1) примет вид
 ,
откуда
,
откуда
 , (4)
, (4)
тогда
 .
.
Общее
количество максимумов равно:
 ,
так как слева и справа от центрального
(
= 0)
будут наблюдаться по
,
так как слева и справа от центрального
(
= 0)
будут наблюдаться по
 максимумов. Окончательно:
максимумов. Окончательно:
 .
.
Ответ: = 6,5 мкм; = 21.
Задача 3. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через поляризатор и анализатор, уменьшилась в четыре раза? Поглощением света пренебречь.
Дано:
|
|
Найти: |
Решение
При прохождении через поляризатор интенсивность естественного света уменьшается вдвое:
 ,
,
где
 –
интенсивность естественного света,
–
интенсивность света, прошедшего через
поляризатор.
–
интенсивность естественного света,
–
интенсивность света, прошедшего через
поляризатор.
При прохождении света через анализатор интенсивность света уменьшается по закону Малюса
,
где – интенсивность света, вышедшего из анализатора, – угол между главными плоскостями поляризатора и анализатора.
По
условию задачи
 ,
следовательно:
,
следовательно:
 ,
,
отсюда
 и
и
 .
.
Ответ: .
Задача 4. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, 0,58 мкм. Определить энергетическую светимость поверхности тела.
-
Дано:
= 0,58 мкм = 5,8∙10-7 м
Найти:

Решение
Энергетическая светимость абсолютно черного тела
,
где – абсолютная температура тела, – постоянная Стефана-Больцмана .
Температуру можно связать с длиной волны законом Вина:
 ,
откуда
,
откуда
 ,
,
где – постоянная Вина . Следовательно,
 .
.
Подставив числовые данные, получим:
 (Вт/м2)
= 35,4 МВт/м2.
(Вт/м2)
= 35,4 МВт/м2.
Ответ: = 35,4 МВт/м2.
Задача
5. В результате эффекта Комптона фотон
при соударении с электроном был рассеян
на угол
 (рис. 9).
Энергия рассеянного фотона
(рис. 9).
Энергия рассеянного фотона
 .
Определить энергию фотона
.
Определить энергию фотона
 до рассеяния.
до рассеяния.
-
Дано:
 =0,4
МэВ
=0,4
МэВ
Рисунок 9
Найти:
Решение
Изменение длины волны фотона, рассеянного на свободном электроне, определяется формулой Комптона:
, (1)
где – длина волны фотона, встретившегося со свободным или слабо связанным электроном, – длина волны фотона, рассеянного на угол после столкновения с электроном, – масса покоящегося электрона.
Учитывая,
что
 и
и
 ,
выразим длины волн
и
через энергии
и
фотонов:
,
выразим длины волн
и
через энергии
и
фотонов:
 ,
или
,
или
 . (2)
. (2)
Из (2) следует, что
 или
или
 . (3)
. (3)
Выразим из полученной формулы искомую величину:
 . (4)
. (4)
Подставим числовые данные, учитывая при этом, что 1 МэВ = 106 эВ = 1,6·10-19·106 Дж = 1,6·10-13 Дж:
 (Дж) = 1,85 МэВ.
(Дж) = 1,85 МэВ.
Ответ: = 1,85 МэВ.
Задача
6. При соударении
- частицы
с ядром
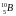 произошла ядерная реакция, в результате
которой образовалось два новых ядра.
Одним из этих ядер было ядро водорода
произошла ядерная реакция, в результате
которой образовалось два новых ядра.
Одним из этих ядер было ядро водорода
 .
Определить порядковый номер и массовое
число второго ядра, дать символическую
запись ядерной реакции и определить ее
энергетический баланс.
.
Определить порядковый номер и массовое
число второго ядра, дать символическую
запись ядерной реакции и определить ее
энергетический баланс.
Решение
Обозначим
неизвестное ядро символом
.
Так как
- частица
представляет собой ядро гелия
 ,
то запись реакции имеет вид
,
то запись реакции имеет вид
 .
.
Применяя законы сохранения числа нуклонов и заряда, получим уравнения
 .
.
Отсюда
 и
и
 .
Следовательно, неизвестное ядро является
ядром атома изотопа углерода
.
Следовательно, неизвестное ядро является
ядром атома изотопа углерода
 .
Теперь можно записать ядерную реакцию
в окончательном виде:
.
Теперь можно записать ядерную реакцию
в окончательном виде:
 .
.
Энергетический баланс ядерной реакции определим по формуле:
 .
.
Здесь
 – сумма масс исходных данных ядер,
– сумма масс исходных данных ядер,
 – сумма масс продуктов реакции.
– сумма масс продуктов реакции.
При
расчетах по этой формуле массы ядер
можно заменить массами нейтральных
атомов. Это возможно по следующей
причине: число электронов в электронной
оболочке нейтрального атома равно его
зарядовому числу
.
Сумма зарядовых чисел исходных ядер
равна сумме зарядовых чисел продуктов
реакции. Следовательно, электронные
оболочки ядер гелия и бора содержат
вместе столько же электронов, сколько
их содержат электронные оболочки ядер
углерода и водорода. Таким образом, при
вычитании суммы масс нейтральных атомов
углерода и водорода из суммы масс атомов
гелия и бора массы электронов выпадут.
Получим тот же результат, как если бы
брали массы только ядер. Подставим массы
атомов в формулу для
 и получим:
и получим:
 МэВ.
МэВ.
Получили
 ,
следовательно, энергетический баланс
указанной ядерной реакции положителен,
т.е. реакция проходит с выделением тепла.
,
следовательно, энергетический баланс
указанной ядерной реакции положителен,
т.е. реакция проходит с выделением тепла.

 =
300
=
300

 =
0,5 м
=
0,5 м

