
Учебное пособие 800669
.pdfи b принимают одно из своих предельных значений в зависимости от знаков величин Ψ и x1/x2.
Траектории минимального и максимального ζ образуют некоторый криволинейный сектор, обладающий тем свойством, что, как бы ни менялись в процессе движения коэффициенты системы (5.90), фазовая точка системы,
находящаяся в начальный момент времени в точке x10, x20, всегда находится внутри этого сектора. Действительно, векторы скорости любой точке, распо-
ложенной на границах криволинейного сектора, т. е. на траекториях мини-
мального и максимального ζ, либо касательны границе, либо направлены внутрь сектора. Это означает, что ни при каких значениях коэффициентов изображающая точка системы не может выйти за пределы сектора. Траекто-
рии, являющиеся границами сектора, по предположению, пересекают линию переключения, так как изображающая точка при любых постоянных значе-
ниях коэффициентов a1(t), a2(t), b(t) попадает на прямую S при любых на-
чальных условиях, а граничные траектории в каждом из квадрантов соответ-
ствуют движению системы с предельными значениями коэффициентов.
При произвольном изменении параметров фазовая точка из начального положения (x10, x20) будет двигаться по траектории, целиком лежащей в кри-
волинейном секторе. Для любойой точки этой траектории можно также по-
строить криволинейный сектор, соответствующий максимальному и мини-
мальному значениям ζ, причем каждый последующий сектор будет лежать внутри предыдущего (рис. 5.24). Площадь сектора, построенного в каждый момент времени и ограниченного траекториями ζmin, ζmax и прямой переклю-
чения S, можно рассматривать как монотонно убывающую функцию P(t).
Случай lim P(t) 0 не может иметь места, так как это означало бы существо-
t
вание дополнительной, кроме начала координат, точки равновесия. Следова-
тельно, либо в некоторый момент времени величина Р будет равна нулю, ли-
бо lim P(t) 0. Это означает, что фазовая точка всегда попадает на прямую пе-
t
501




личин x1 и u со скачкообразно меняющимися коэффициентами |
|
||||
v x x |
|
uu, |
(5.114) |
||
|
1 |
|
|
|
|
где |
|
|
|
|
|
|
x |
при zx |
0, |
|
|
|
|
(5.115) |
|||
x |
|
|
1 |
0, |
|
x |
при zx |
|
|||
|
|
|
1 |
|
|
|
u |
при zx |
0, |
|
|
|
|
(5.116) |
|||
u |
|
|
1 |
0, |
|
u |
при zx |
|
|||
|
|
|
1 |
|
|
z cx1 x2; |
|
(5.117) |
|||
αx, βx, αu, βu, c – постоянные величины.
Выберем коэффициенты αx, βx, αu, βu, определяющие четыре возможные линейные структуры такими, чтобы для рассматриваемого процесса регули-
рования обеспечивалось выполнение условий /75/
lim z 0, |
lim z 0. |
(5.118) |
z 0 |
z 0 |
|
существования скользящего режима для любой точки прямой S (S - прямая,
заданная на плоскости (x1,x2) уравнением z= 0) и попадание изображающей точки на S.
Совершенно так же, как это уже неоднократно делалось в рассматри-
ваемых ранее случаях, из (5.113), (5.114) и (5.117) определим величину z на прямой S:
|
|
b1 |
x)x ( |
b2 |
|
b2 |
u )u. |
(5.119) |
|
z ( c2 ca |
a |
b |
|||||||
T |
T |
|
|||||||
2 |
1 |
1 |
1 |
T |
|
||||
Потребуем, чтобы для слагаемых в (5.119) выполнялись соответственно неравенства
( c2 ca |
|
|
a |
b1 |
x )x z 0, |
|
|
||||||
2 |
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
T |
|
|
(5.120) |
|
|
b2 |
|
|
b2 |
|
|
|
|
|
||||
( |
b1 |
|
|
u |
)uz 0. |
|
|
|
|||||
T |
|
|
T |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Из (5.120) с учетом (5.115), (5.116) получаем расчетные соотношения,
позволяющие выбрать параметры управляющего устройства αx, βx, αu, βu, c
507
так, чтобы прямая S была прямой скольжения:
x max |
T |
|
[ c2 |
ca |
|
a ], |
|
|
|||
|
|
|
|
||||||||
a1,a2,b2 b |
|
|
|
|
2 |
1 |
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
x min |
[ c2 |
ca |
a (t)], |
|
|||||||
|
|
||||||||||
a1,a2 ,b2 |
b2 |
|
|
|
|
2 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
(5.121) |
|
u max[1 T |
b1 |
], |
|
|
|
||||||
|
|
|
|
||||||||
b2 |
|
|
|
||||||||
b1,b2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
b |
|
|
|
|
|
||
u min[1 T |
|
|
|
|
|
||||||
1 |
], |
|
|
|
|
||||||
|
|
|
|
||||||||
b1,b2 |
|
|
|
b2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, если каждое из двух возможных значений коэффици-
ентов Ψx и Ψu удовлетворяет (5.121), то после попадания фазовой точки на S
дальнейшее изменение координаты не будет зависеть от переменных коэф-
фициентов системы (5.113) и, как всегда, в скользящем режиме однородное дифференциальное уравнение с постоянными коэффициентами
cx1 x2 0
определяет закон изменения координат x1, x2, причем коэффициент с выбира-
ется в соответствии с каким-либо заданным критерием качества переходных процессов.
Как и для системы с постоянными параметрами, работоспособность системы с переменными параметрами определяется с учетом закона измене-
ния величины u при движении фазовой точки по прямой S. С этой целью из
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(5.113) и (5.117) определим величину z: |
|
|
|
|
|
|
|
|
|
|
||||||||
z (c a (t))x a (t)x b2 (t) b (t) u b2 (t)v. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
T |
|
|
T |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Поскольку в скользящем режиме z |
= 0, то |
|
|
|
|
|
|
|||||||||||
v |
T |
c a |
2 |
(t) x |
2 |
T |
a1(t) |
x |
1 T |
|
b1 |
(t) |
u. |
|||||
|
|
|
|
|||||||||||||||
|
b2 (t) |
|
|
|
b2 |
(t) |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
b2 (t) |
||||||||
Подставляя найденное значение u в последнее уравнение системы
(5.113), получаем
508

вующей в системе с постоянными параметрами.
При этом удалось не только построить систему, качественные показа-
тели процесса управления в которой с изменением ai(t), bi(t) в пределах
(5.111) меняются незначительно, но и избежать применения настройки пара-
метров управляющего устройства в зависимости от нестационарных характе-
ристик объекта. Увеличение объема информации о состоянии нестационар-
ной системы, используемой в процессе управления, объясняется тем, что введение в управляющее устройство фильтра приводит к повышению поряд-
ка системы. При этом поведение системы полностью определяется тремя ко-
ординатами x1, x2,u. Однако это не приводит к существенному техническому усложнению системы, так как координату u (по сути дела, выходную коор-
динату инерционного звена) всегда можно измерить тем или другим спосо-
бом.
5.3.3. Применение метода разделения движений
к синтезу систем автоматического управления.
Методы фазового пространства позволяют исследовать системы с ши-
роким классом нелинейностей, но ограничивают порядок уравнений до третьего /95/.
«Метод разделения движения» расширяет возможности применения методов фазового пространства и является одним из возможных способов использования метода фазовой плоскости для анализа автоматических сис-
тем высокого порядка /96/. Основа метода – разделение полного движения системы на быстрые и медленные составляющие. При этом быстрым движе-
ниям соответствует система уравнений меньшего порядка, чем исходная сис-
тема; медленным движениям – система уравнений также невысокого поряд-
ка.
Рассмотрим нелинейные автоматические системы, работающие по замкнутому циклу.
510


 b x
b x
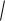 b
b
 ab
ab
 x
x