Учебное пособие 800657

ассоциативной памяти.

Сеть Хопфилда [20] является автоассоциативной сетью (рис. 4.12). Дискретная сеть Хопфилда имеет следующие характеристики: она содержит один слой элементов; каждый элемент связывается со всеми другими элементами, но не связан с самим собой; за один шаг работы обновляется только один элемент сети; элементы обновляются в случайном порядке; выход элемента ограничен значениями 0 или 1.

Рис. 4.12. Схема архитектуры модифицированной сети Хопфилда

Пример решения типовой задачи

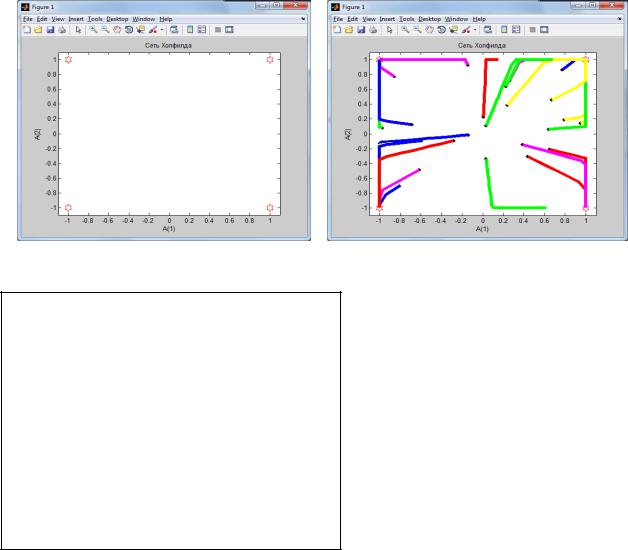
Рассмотрим сеть Хопфилда [27] с четырьмя нейронами и определим четыре точки равновесия (рис. 4.13):

Отчет о выполнении лабораторной работы № 4 должен быть выпол-

нен на листах формата А4 и содержать следующие результаты:

1)исходные данные;

2)текст программы с подробными комментариями;

3)результаты моделирования (рис. 4.13);

4)контрольный пример;

5)краткие письменные ответы на контрольные вопросы, содержащиеся в приложении.

Лабораторная работа № 5 Формирование нечетких множеств и проведение операций с ними

Цель работы: изучить методы построения нечетких множеств с использованием различных типов функций принадлежности. Ознакомиться с наиболее распространенными логическими операциями над нечеткими множествами.

Краткие теоретические сведения

Функции принадлежности. Инструменты нечеткой логики в составе пакета Matlab содержат 11 встроенных типов функций принадлежности, формируемых на основе кусочно-линейных функций, распределения Гаусса, сигмоидной кривой, квадратических и кубических полиномиальных кривых. К наиболее простым функциям принадлежности можно отнести треугольную и трапециевидную.

Рис. 4.14. Треугольная (а) и трапециевидная (б) функции принадлежности

Треугольная функция принадлежности – (triangle membership function) в параметрическом виде представляет собой набор трех точек, образующих треугольник.

= , [ ] ;

где вектор – базовое множество, на котором определяется функция принадлежности. Величины и задают основание треугольника, – его вершину.

В аналитическом виде треугольная функций принадлежности может быть задана следующим образом (рис. 4.14, а):

123

0, если < ;

−

0, если > .

Рассмотрим примеры использования различных функций принадлежности в системе Matlab.

Примеры решения типовой задачи Пример 4.1. Программа использования функций принадлежности .

Трапециевидная функция принадлежности – (trapezoid membership function) – отличается от предыдущей функции лишь тем, что имеет верхнее основание.

= , ;

где параметры и – нижнее основание трапеции; и с – верхнее основание трапеции (рис. 4.14, б).

Аналитическая запись трапециевидной функции имеет вид

0, если < ;

−− , если ≤ ≤ ;

, , , , = 1, если < ≤ ; (4.16)

−

− , если < ≤ ;

0, если > .

Одно из основных достоинств треугольных и трапециевидных функций принадлежности – их простота. На основе функции распределения Гаусса можно построить функции принадлежности двух видов: простую функцию принадлежности Гаусса и двухстороннюю, образованную с помощью различных функций распределения Гаусса. Первая из них обозначается

, а вторая – 2 .

Рис. 4.15. Простая (а) и двухсторонняя (б) функции принадлежности Гаусса

Пример 4.2. Программа использования функции принадлежности

.

= 0: 0.1: 10;

= , 2 5 ;, ;

Описание функции: у = 2 ( , [ 1, 1, 2, 2]). Выражение является комбинацией двух различных функций распределения Гаусса. Первая определяется параметрами 1 и 1 и задает форму левой стороны, а вторая (параметры 2, 2,) – правой стороны функции принадлежности. Если < 2, то функция 2 достигает своего максимального значения на уровне 1. Иначе – максимальное значение функции меньше 1 (рис. 4.15, б).

Пример 4.3. Программа использования функции принадлежности

2 .

= (0 0,1 10) ′ ;1 = 2 ( , [2 4 18]);

у2 = 2 ( , [2 5 17]); уЗ = 2 ( , [2 6 16]); у4 = 2 ( , [2 7 15]); у5 = 2 ( , [2 8 14]);( , [ 1 у2 уЗ у4 у5]);

Символ « ′ » в строке определения базового множества показывает транспонированность базового множества.

Следующей функцией, которая позволяет представлять нечеткие субъек-

125

тивные предпочтения, является функция принадлежности «обобщенный коло-

кол» и обозначается (generalized bell shape membership function). Ее от-

личие от рассмотренных ранее функций принадлежности заключается в добавлении третьего параметра, что позволяет осуществлять плавный переход между нечеткими множествами.

= , ;

Функция «обобщенный колокол» зависит от трех параметров и имеет следующую аналитическую запись:

1, , , = 1 + − 2 , (4.18)

где определяет расположение центра функции принадлежности; и влияют на форму кривой (рис.4.16).

Рис. 4.16. Функция принадлежности «обобщенный колокол»

, = [2 4 6]

Пример 4.4. Программа использования .

= 0 0,1 10; у = ( , [2 4 6]);

( , у);′, = 2 4 6 ′ ;

Функции принадлежности на основе функции распределения Гаусса и функции принадлежности «обобщенный колокол» отличаются гладкостью и простотой записи. Они являются наиболее используемыми при описании нечетких множеств. Несмотря на то, что гауссовы и колоколообразные функции принадлежности обладают свойством гладкости, они не позволяют формировать асимметричные функции принадлежности. Для этих целей предусмотрен

126

набор сигмоидальных функций, которые могут быть открыты либо слева, либо справа в зависимости от типа функции. Симметричные и закрытые функции синтезируют с использованием двух дополнительных сигмоид. Основная сигмоидальная функция принадлежности обозначается , а дополнительные –

и .

В зависимости от знака параметра рассматриваемая функция принадлежности будет открыта или справа или слева (рис. 4.17, a), что позволит применять ее при описании таких нечетких понятий, как «очень большой», «крайне

у = ( , [ 1, 1, 2, 2]). Функция принадлежности зависит от четырех параметров 1, 1, 2 и 2 и определяется как разность двух сигмои-

1( , 1, 1) 2{ , 2, 2) (рис. 4.17, в).

Рис. 4.17. Сигмоидальные функции принадлежности:

– основная односторонняя; б – дополнительная двухсторонняя;

в– дополнительная несимметричная

127

Пример 4.5. Программа использования сигмоидных функций (рис. 4.18).

( ′, = [2 3 − 5 8]′);

Рис. 4.18. Полиномиальные функции принадлежности: а – - функция; б – - функция; в – - функция

Инструментарий нечеткой логики (fuzzy logic toolbox) в составе Matlab предоставляет возможность формирования функции принадлежности на основе полиномиальных кривых. Соответствующие функции называются - функциями ( ), -функциями ( ) и 5-функциями ( ). Функция представляет собой асимметричную полиномиальную кривую, открытую слева

128

(рис. 4.18, а), функция – зеркальное отображение функции (рис. 4.18, б). Соответственно функция равна нулю в правом и левом пределах и принимает значение, равное единице, в середине некоторого отрезка

(рис. 4.18, в).

= , ;

Параметры и определяют экстремальные значения кривой (рис. 4.18, а).

= , с ;

Параметры и задают переход функции в нулевое значение, а параметры и — в единичное (рис. 4.18, б).

= , ;

Параметры а и b определяют экстремальные значения кривой (рис. 4.18, в). Пример 4.6. Программа использования полиномиальных кривых.

= 0: 0,1: 10;(1, 3, 1);

= ( , [3 7]); ( , ); (′, = [3 7]′);(1, 3, 2);

= ( , [1 4 5 10]); ( , ); (′, = [1 4 5 10]′);(1, 3, 3);

= ( , [1 8 ]); ( , ); ′, = 1 8 ′ ;

Помимо рассмотренных выше функций, позволяющих представлять нечеткие множества, в Matlab имеется возможность формировать собственные функции принадлежности или модифицировать встроенные.

Операции с нечеткими множествами

Выделяют три основные логические операции с нечеткими множествами: конъюнкцию, дизъюнкцию и логическое отрицание. В среде Matlab существует возможность определять конъюнктивные и дизъюнктивные операторы с точки зрения минимаксной и вероятностной интерпретаций.

Рассмотрим минимаксную интерпретацию логических операторов, в которой конъюнктивный оператор представляет нахождение минимума – (рис. 4.19, а), а дизъюнктивный – нахождение максимума – (рис. 4.19, б).

= 1; 2 ,

= ([ 1; 2]).

Параметры 1 и 2 представляют собой исходные функции принадлежности. Функция работает со списком функций принадлежности. В Matlab список оформляется квадратными скобками, а элементы списка разделяются точкой с запятой.

129

Рис. 4.19. Пересечение (а) и объединение (б) нечетких множеств (минимаксная интерпретация)

Пример 4.7. Программа использования операций и .

= 0: 0,1: 10;(1, 2, 1);

1 = ( , [3 5]); 2 = ( , [3 7]);З = ( [ 1; 2]); ( , [ 1; 2], ′: ′)

; ( , З); ;

(1, 2, 2);4 = ([ 1; 2]); ( , [ 1; 2] , ′: ′) ;

; ( , 4); ;

Пунктирной линией на графиках изображены исходные функции принадлежности, а сплошной линией – результат действия логических операторов.

Минимаксная интерпретация является наиболее распространенной при построении нечетких систем. Тем не менее, на практике довольно часто используется альтернативная вероятностная интерпретация конъюнктивных и дизъюнктивных операторов. Matlab содержит соответствующие функции.

алгебраической суммы — (рис. 4.20, б).

= 1 ; 2 ,= ([ 1; 2]).

130