Учебное пособие 800533

С.А. Кострюков В.В. Пешков Г.Е. Шунин В.А. Шунина

ПРАКТИКУМ ПО ЧИСЛЕННЫМ МЕТОДАМ

Учебное пособие

Воронеж 2017

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВО «Воронежский государственный технический университет»

С.А. Кострюков В.В. Пешков Г.Е. Шунин В.А. Шунина

ПРАКТИКУМ ПО ЧИСЛЕННЫМ МЕТОДАМ

Утверждено учебно-методическим советом университета в качестве учебного пособия

Воронеж 2017

ВВЕДЕНИЕ

С точки зрения математического моделирования решение физико-технической задачи сводится к решению математической задачи, являющейся ее моделью. Для решения математических задач в основном используются аналитические, графические и численные методы.

Аналитические методы позволяют представить решение в виде формул. С помощью графических методов решение получается в виде графических построений. Численные методы сводят решение математической задачи к выполнению конечного числа арифметических операций над числами, и результаты при этом представляются в виде чисел. Именно спомощью численных методов решается подавляющее число современных сложных задач физико-математического моделирования. Основную роль в этом сыграло появление высокопроизводительных компьютеров, способных выполнять миллиарды, триллионы и более операций в секунду.

В настоящее время имеется значительное число программных продуктов, ориентированных на решение задач вы-

числительной математики (MathCad, Maple, Mathematica, и

т.д.) Конечно, умение пользоваться готовыми программами сокращает время и затраты на решение важных практических задач. С другой стороны, для их использования зачастую достаточно лишь задания входных данных без вникания в сущность методов и алгоритмов, заложенных в программу. Как правило, выбор метода, проведение расчетов, выдачу результатов программа берет на себя. Однако при таком подходе полученное решение носит обычно приближенный характер, поскольку каждая модель и каждый метод имеют существенные ограничения по применимости. Кроме того, незнание метода не дает возможности проанализировать решение (оценить погрешность решения, скорость сходимости, устойчивость и др.) Таким образом, грамотный специалист должен иметь представление об основах математического моделирования, численных методов, о возможностях современных программных

3

средств, уметь анализировать полученные результаты с точки зрения их точности и достоверности.

В данном учебном пособии рассмотрены основные численные алгоритмы решения математических задач, таких как решение линейных и нелинейных уравнений, интегрирование и дифференцирование, интерполирование, точечная и непрерывная аппроксимации функций, решение дифференциальных уравнений.

Как известно, многие задачи моделирования физических процессов сводятся к решению дифференциальных уравнений. Причем аналитически может быть решен только ограниченный класс таких уравнений. Традиционный подход численного решения связан к переходу к конечным разностям. Однако более эффективными методами решения, в частности, краевых задач, в настоящее время признаются методы, базирующиеся на аппроксимации базисными функциями. Поэтому этим методам в пособии уделено особое внимание. Подробно рассмотрены методы: вариационный (метод Ритца), проекционный (метод Галеркина), вариационно-разностный (метод конечных элементов). Для них даны четкие критерии сходимости аппроксимации.

Особенностью пособия является его практическая направленность. Большинство примеров разбираются в пошаговом режиме с использованием одной из популярных сиcтем компьютерной математики – Maple. Такой подход способствует лучшему усвоению методов, не отвлекаясь на рутинные вычисления.

Учебное пособие может быть использовано преподавателями, аспирантами и студентами физико-технических специальностей вузов.

4

1.РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

ИСИСТЕМ УРАВНЕНИЙ

1.1.Понятие о линейных и нелинейных уравнениях

в котором g(x) – некоторая функция, x является неизвестной переменной, а b – некоторое число. Решением (корнем) этого уравнения называется всякое число x из области определения g(x), которое, будучи подставлено в уравнение (1.1), обращает его в тождество. Под термином «решение уравнения» также понимают процесс нахождения (вычисления) его корней. Решить уравнение – значит найти совокупность (множество) всех его корней. Иногда задача ставится о решении уравнения лишь на каком-либо подмножестве числовой оси x (например, на отрезке), тогда ищется совокупность корней уравнения, принадлежащих этому подмножеству.

Пусть x, b – векторы размерности n, тогда приходим к системе уравнений

g1(x1,x2, ,xn) b1 , g2(x1,x2, ,xn) b2 ,

…………………….

gn(x1,x2, ,xn) bn ,

В этом случае решением является не число, а числовой вектор x* (x1, x2,..., xn)*.

Линейные уравнения вида (1.1) или (1.2) характеризуются важным свойством: функция g(x) (или вектор-функция g(x)) удовлетворяет принципу суперпозиции, состоящему в том, что если аргумент x есть линейная комбинация (суперпозиция) двух точек

5

x c1x(1) c2x(2) ,

где c1 и c2 – константы, то значение g(x) есть линейная суперпозиция значений g(x(1)) и g(x(2)), а именно

Легко проверить выполнение этого принципа для функций g(x)=ax (a = const) и g(x)=Ax, где A – матрица размером n n.

Нелинейные функции не удовлетворяют принципу суперпозиции, например, для g=x2 (1.3) не выполняется:

(c1x1 c2x2)2 c1x12 c2x22

Этот факт лежит в основе различия линейных или нелинейных уравнений.

Линейные уравнения могут иметь:

1)единственное решение;

2)бесконечное множество решений;

3)не иметь решений вовсе.

Линейные уравнения являются частным случаем нелинейных, поэтому для нелинейных уравнений возможны упомянутые выше три варианта, а также

4) имеется n решений, 2 n< .

Примером четвертого варианта могут служить задачи определения корней полиномов Pn(x)=a0 +a1x+a2x2 +…+anxn.

Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.

Нелинейные уравнения принято записывать в виде

который получается из (1.1) путем замены f(x) g(x) – b.

6

1.2. О методах решения нелинейных уравнений

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры читателю известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако встречающиеся на практике уравнения часто не удается решить такими простыми методами. Для их решения используются итерационные методы, т.е. методы последовательных приближений. Алгоритм нахождения корня нелинейного корня нелинейного уравнения с помощью итерационного метода состоит из двух этапов: а) отыскания приближенного значения корня (начального приближения); б) уточнения приближенного значения до некоторой заданной степени точности. В некоторых методах отыскивается не начальное приближение, а некоторый отрезок, содержащий корень.

Общая схема итерационных методов состоит в последовательном уточнении начального приближения x0. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня x1, x2,…, xk. Если эти значения с ростом k стремятся к истинному значению корня

lim xk x*,

k

то говорят, что итерационный процесс сходится.

Прежде чем приступить к вычислительной процедуре решения уравнения, определяют отрезки числовой оси, содержащие по одному корню данного уравнения, или, как говорят, отделяют корни. Для отделения корней уравнения можно использовать критерий: если на отрезке [a, b] функция f(x) непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на этом отрезке существует и притом один корень данного уравнения. Достаточным признаком монотонности функции f(x) на отрезке [a, b] является сохранение знака

7

производной функции. При отделении корней стараются определить отрезок [a, b] как можно меньшей длины.

Отделение корней можно выполнить также графически. Найти корень уравнения (1.4) – это значит найти абсциссу точки пересечения графика функции y=f(x) с прямой y=0 (осью абсцисс). Если построить график функции затруднительно, то уравнение (4) следует представить в эквивалентном виде

с таким расчетом, чтобы графики функций f1(x) и f2(x) строились проще. Корни же уравнения (1.5) определяются как абсциссы точек пересечения графиков функций y = f1(x) и y = f2(x). Если уравнения (1.4) и (1.5) эквивалентны, то, отделив корни уравнения (1.5), мы тем самым отделяем и корни уравнения

(1.4).

Выбор алгоритма построения последовательности {xk}, или метода решения, – весьма важный момент при практическом решении задачи. Здесь немалую роль играют такие свойства алгоритма, как простота, надежность, экономичность и т.д.

Одной из характеристик вычислительного алгоритма является его скорость сходимости. Последовательность{xk}, сходящаяся к пределу x* (x*≠x1), имеет порядок сходимости≥1, если существуют числа c≥0, k0 >0, ≥1 такие, что для всех k≥k0

|xk 1 x*| c| xk x*| .

Сходимость при =1 называется линейной, или 1-го порядка, при =2 – квадратичной и т.д. С ростом вычислительный алгоритм построения последовательности {xk} усложняется, и условия, обеспечивающие сходимость последовательности {xk}, становятся более жесткими.

На практике чаще всего используются следующие методы решения нелинейных уравнений: половинного деления, секущих (хорд), простой итерации, парабол, Ньютона.

8

1.3.Решение нелинейных уравнений

1.3.1.Метод деления отрезка пополам

Простейшим и надежным алгоритмом уточнения корня является метод деления отрезка пополам (или бисекции). Пусть на отрезке [a, b] функция f(x) непрерывна и на концах этого отрезка имеет разные знаки, т.е. f(a)f(b)<0. Очевидно, что середина отрезка служит приближением к корню уравнения (1.4) с точностью (b–a)/2. В середине отрезка x1 =(a+b)/2 определяется знак функции f(x), затем выбирается та половина отрезка, на концах которой функция f(x) принимает значения разных знаков, и деление повторяется. Если требуется найти корень с точностью , то деление отрезка пополам продолжается до тех пор, пока длина отрезка не станет меньше 2 . Тогда середина последнего отрезка даст значение корня с требуемой точностью.

Алгоритм метода:

1.Найти x a b 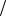2.

2.Вычислить f(x).

перейти к пункту 1, если оно не выполняется, закончить вычисления, считая корнем x с точностью .

Метод деления отрезка пополам имеет линейную скорость сходимости.

Пример. Решить уравнение 0.5x +2=(x–2)2.

Решение в системе компьютерной математики Maple

Документ пакета Maple рекомендуется начинать с команды очистки оперативной памяти:

>restart;

1)Задаем функцию f(x)=0,5x +2–(x–2)2:

>f:=t->0.5^t+2-(t-2)^2;

2)Отделяем корни, для этого строим график функции f(x). Поскольку заранее неизвестно, на каком промежутке (или

9