Учебное пособие 800519

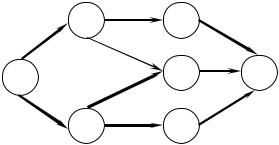
4.Сокращаем продолжительность работы (4,6) на Δ=16 единиц.

Соответственно ее объем на 3,2 единицы. x346 3.8. Затраты увеличились на

3.210 32 единицы и стали равны c(x3 ) 72.

5.Поскольку Т(х3)=33>30, то повторяем шаги алгоритма.

1.Сеть критических путей показана на рис. 2.1.1.3.

2.Множество V(x3 ) {(4,6),(3.6)}. Пропускная способность разреза равна 4.

3.Определяем . Заметим, что при Δ=1 в сети появляется еще один критический путь (0,2,5,6). Берем Δ=1.

4.Сокращаем продолжительности работ (3,6) и (4,6) на 1. Соответственно их

Рис. 2.1.1.4

2.Множество V(x4 ) {(3,6)(4,6),(5,6)}. Пропускная способность разреза равна 5.

3.Определяем . Поскольку Т(х4)-Т=2, то Δ=3.

4.Сокращаем продолжительности работ (3,6), (4,6) и (5,6) на 2 единицы. Соответственно их объемы уменьшим на 2/3 (для работы (3,6)), на 0,4 единицы для работы (4,6) и на 1/3 единицы для работы 5,6). Затраты увеличились на

(5,6), то есть на 10 единиц, что составляет c(x5 ) 76 10 86 единиц. 5. Поскольку Т(х5)=30=Т, то задача решена.

Оптимальные объемы работ, выполняемых своими силами, ( yij Wij xij )

объемы работ, передаваемые на субподряд, и дополнительные затраты приведены в табл. 2.1.1.3.

51

Таблица 2.1.1.3

2.1.2.Независимые работы. Степенной случай

Впредыдущей модели не учитывалась возможность использования освобождающихся ресурсов на других работах проекта. Рассмотрим ряд простых моделей, учитывающих эту возможность. Пусть работы проекта

независимы, а скорости работ wij являются степенными функциями количества ресурсов ui :

wij uij1 , где α>1.

Количество ресурсов ограничено и равно N. Рассмотрим сначала случай α=2. В случае независимых работ и вогнутых зависимостей скоростей работ от количества ресурсов оптимальное решение по критерию минимума времени удовлетворяет следующим двум условиям:

1.Все работы начинаются и заканчиваются одновременно.

2.Все работы выполняются с постоянной интенсивностью.

Пусть Т(х) − минимальная продолжительность проекта при объемах х. Имеем

Из ограничения Т(х)≤Т получаем

Целевая функция имеет вид

Таблица 2.1.2.1

Дополнительные затраты

C(x) 4 2 5 6 38 .

Обобщим решение для случая произвольного α>1. По аналогии с предыдущими выкладками, получаем

Из ограничения T(x) T получаем

Множитель λ определяем из уравнения

Далее алгоритм работает аналогично описанному выше.

2.1.3. Независимые работы. Линейный случай

Рассмотрим линейный случай, когда зависимость скоростей работ от

wi

wi

T(Q1 ) T(Q2 ) ... T(Qk ) ,

поскольку количество ресурсов на работах множества Qj увеличивается с

не может быть пустым. В силу монотонного уменьшения числа работ множеств Qj с ростом j процедура конечна.

Пример 2.1.3.1. Имеются 5 работ, данные о которых приведены в табл. 2.1.3.1.

Таблица 2.1.3.1

Примем N=12. 1шаг. Вычисляем

Рассмотрим алгоритм решения задачи определения оптимальных объемов работ.

2случай. T T(Q) .

Вэтом случае объемы всех работ i Q должны быть сокращены на iai ,

где i i T и равны xi w i i ai .

Что касается работ i Q , то для определения оптимальных объемов необходимо решить задачу максимизации

C(x, Q) ci xi ,

i Q

при ограничениях

0 xi ai min( T, i ) bi , i Q ,

2. Полагаем

xi aibi , i 1,k 1,

k 1

xk (k 1)D xi ,

1

xi 0, i k 1,n .

57

Обоснование алгоритма

Обоснование алгоритма следует из того, что, во-первых, xi D, а, во

i Q

вторых, для всех xi имеет место xi bi и, следовательно, все работы будут

выполнены за время Т. Оптимальность легко следует из вида задачи линейного программирования.

Пример 2.1.3.2. Возьмем данные из примера. Примем Т=2,5. Имеем: b1=2,5, b2=2, b5=2. Вычисляем

D NT 5 7,5 17,5. a1b1 7,5 17,5 ,

a1b1 a2b2 15,5 17,5 , a1b1 a2 b2 a5b5 25,5 17,5 ,

Таким образом, k=3.

Получаем оптимальное решение х1=7,5, х2=8, х3=5, х4=7,5, х5=2. Соответственно объем работ, отдаваемых на субподряд, составит у1=1,5, у2=0, у3=7, у4=7,5, у5=8, а дополнительные затраты

Сmin=7,5+0+21+15+8=51,5.

2.1.4. Потоковая модель

До сих пор мы рассматривали задачи с постоянным уровнем ресурсов N. Рассмотрим модель с переменным уровнем ресурсов. А именно примем, что отрезок [0,Т] разбит на m отрезков постоянства уровней ресурсов. Обозначим Nk - количество ресурсов в k-м интервале. Кроме того, примем, что работа i может выполняться в промежутке от интервала diдо интервала Diвключительно. Ограничимся линейным случаем. По-прежнему считаем, что работы пронумерованы по убыванию коэффициентов сi.

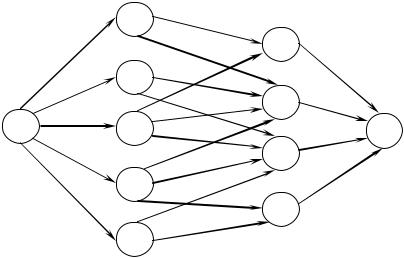
Определим сеть из (n+m+z) вершин, состоящую из входа 0, n вершин первого слоя, m вершин второго слоя и выхода z. На рис. 2.1.4.1. приведен пример такой сети для случая n=5, m=4.

Рис. 2.1.4.1

58

Вершина 0 соединена со всеми вершинами первого слоя дугами (0,i) пропускной способности P0i Wi . Вершина i первого слоя соединена с

вершиной j второго слоя дугой (i, j), если работа i может выполняться в

где Ri – множество дуг, исходящих из вершины i первого слоя.

где Ро – множество дуг, заходящих в вершинуjвторого слоя.

Заметим, что любому потоку {xij} однозначно соответствует допустимое распределение объемов работ по периодам. И наоборот, любому допустимому распределению работ по периодам однозначно соответствует поток в сети.

Задача заключается в определении потока, минимизирующего

C(x) wi x0i ci

i

или максимизирующего

Ф(x) ci x0i .

i

Описание алгоритма

1шаг. Определяем поток максимальной величины, проходящей по дуге (0,1) первого слоя.

2 шаг. Определяем поток максимальной величины, проходящей по дуге (0,2) первого и не уменьшающей величины потока по дуге (0,1) первого слоя.

k шаг. Определяем поток максимальной величины, проходящей по дуге (0,k) первого слоя и не уменьшающей величины потоков по дугам (0,i) первого слоя (i<k).

Теорема 2.1.4.1. Описанный выше алгоритм дает оптимальное решение задачи. Доказательство. Поток по любой дуге (0,k) первого слоя можно увеличить только за счет уменьшения на ту же величину потоков по дугам (0,i) первого

59

слоя, где i<k. Но это не приведет к уменьшению затрат, поскольку Ci Ck для всех i<k. Это доказывает теорему.

Пример 2.1.4.1. Имеются 5 работ, данные о которых приведены в табл. 2.1.4.1.

Примем Т=9.

Длительности интервалов и уровни ресурсов указаны в табл. 2.1.4.2.

Таблица 2.1.4.2

Потоковая сеть приведена на рис. 2.1.4.1 (в скобках указаны пропускные способности дуг)

1шаг. Определяем поток максимальной величины по дуге (0,1). Возможный вариант

x11 9, x12 3 (указано без скобок у дуг), x01 12 . 2 шаг. Определяем поток максимальной величины по дуге (0,2).

x22 12, x23 5 , x02 17 .

3 шаг. Определяем поток максимальной величины по дуге (0,3).

x31 9, x32 5, x33 0 , x03 14 .

4 шаг. Определяем поток максимальной величины по дуге (0,4).

x42 0, x43 0, x44 9 , x04 9 .

5 шаг. Определяем поток максимальной величины по дуге (0,5).

x53 0, x54 9 , x05 9 .

Объемы работ, передаваемых на субподряд равны

у1=0, у2=1, у3=10, у4=6, у5=0,

затраты составляют

С(х)=0+4+30+12+0=46.

60