
Теория автоматического управления. Лабораторный практикум в среде Matlab. учебное пособие. Харченко А.П., Слепокуров Ю.С
.pdf
5.Как влияет коэффициент передачи К и по времени постоянная времени Т на временные и частотные характеристики типового звена 2-го порядка?
6.Как влияет коэффициент демпфирования Do на временные и частотные характеристики типового звена 2-го порядка?
ЛАБОРАТОРНАЯ РАБОТА № 3
ИCСЛЕДОВАНИЕ ОДНОКОНТУРНОЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель работы: исследование системы автоматического управления с жесткой и гибкой отрицательной обратной связью.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Применение отрицательных обратных связей (ООС) в системах автоматического управления (САУ) позволяет изменять вид ЛАЧХ и параметры переходной характеристики замкнутой САУ.
На рис. 15 представлена структурная схема с ООС, с передаточной функцией прямой цепи Wпр(p) и в обратной цепи
– Wос(p).
Жесткая отрицательная обратная связь (ЖООС) действует все время, а гибкая (ГООС) – не действует при отсутствии скорости изменения выходного сигнала dу(t) /dt охватываемого звена.
Х(p) |
|
|
|
У(p) |
||
|
|
|
||||
|
|
|
|
Wпр(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wос(p)
Рис. 15. Структурная схема с ООС
21
Пусть апериодическое звено первого порядка охвачено ЖООС, то есть в цепи ООС включено позиционное звено, например пропорциональное.
Пусть такое же апериодическое звено охвачено ГООС, то есть в цепи ООС включено дифференцирующее звено с замедлением. В случае ЖООС передаточная функция замкнутой системы при p = 0 определяется
W(p = 0) = Ко = Кпр / (1 + Кпр*Кос),
где Кпр, Кос – коэффициенты передачи звеньев в прямой и обратной цепях структурной схемы; Ко – коэффициент передачи системы.
В результате охвата звена ЖООС общий коэффициент передачи уменьшился, такое введение ООС эквивалентно включению в систему форсирующего звена.
Во случае ГООС передаточная функция замкнутой системы при p = 0 определяется
W(p) = Кпр.
В этом случае общий коэффициент передачи системы не изменился, а в динамическом отношении введение ГООС эквивалентно включению в структурную схему системы с ООС последовательного замедляющего корректирующего звена.
Использование ГООС в технических системах позволяет регулировать не только выходную величину, но и скорость ее изменения.
При использовании ЖООС в САУ и выполнении условия Кпр*Кос » 1 коэффициент передачи системы определяется
Ко = Кпр / Кпр*Кос = 1/ Кос.
Использование ГООС в САУ позволяет реализовать управление по скорости изменения выходной величины. В этом случае САУ в установившемся режиме работы функцио-
22
нирует как разомкнутая, а в переходном режиме работы, как замкнутая.
ПРЕДВАРИТЕЛЬНОЕ ЗАДАНИЕ
1.Определить передаточную функцию замкнутой и разомкнутой САУ для значений передаточной функции прямой и обратной цепи, представленных в табл. 3 – 4.
2.Для элементов САУ, заданных табл. 3 положить, что в обратной связи позиционное (пропорциональное) звено с коэффициентом передачи Кос.
3.Для параметров элементов САУ, заданных табл. 4 положить, что в обратной цепи позиционное звено с коэффициентом передачи Кос1.
4.Для параметров элементов САУ заданных табл. 4 положить, что в обратной цепи реальное дифференцирующее звено с коэффициентом передачи Кос2 и постоянной времени Тос.
5.Определить передаточную функцию САУ при p = 0.
|
|
|
|
|
Таблица 3 |
||
|
Параметры передаточной функции САУ |
|
|
|
|||
|
|
|
|
|
|
|
|
Вариант |
Интегрирующе |
ЖООС |
Апериодическое |
|
ЖООС |
|
|
звено |
|
звено |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Кпр |
Кос |
Кпр |
Тпр |
|
Кос |
|
|
|
|
|
|
|
|
|
1 |
100 |
1 |
1 |
0.1 |
|
1 |
|
2 |
100 |
2 |
1 |
0.1 |
|
2 |
|
3 |
100 |
3 |
1 |
0.1 |
|
3 |
|
4 |
100 |
4 |
1 |
0.1 |
|
4 |
|
5 |
100 |
5 |
1 |
0.1 |
|
5 |
|
6 |
100 |
6 |
1 |
0.1 |
|
6 |
|
7 |
100 |
7 |
1 |
0.1 |
|
7 |
|
8 |
100 |
8 |
1 |
0.1 |
|
8 |
|
23
Окончание табл. 3
9 |
100 |
9 |
1 |
0.1 |
9 |
10 |
100 |
10 |
1 |
0.1 |
10 |
11 |
1000 |
0.1 |
10 |
0.1 |
0.1 |
12 |
1000 |
0.2 |
10 |
0.1 |
0.2 |
13 |
1000 |
0.3 |
10 |
0.1 |
0.3 |
14 |
1000 |
0.4 |
10 |
0.1 |
0.4 |
15 |
1000 |
0.5 |
10 |
0.1 |
0.5 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
1. Задать структурную схему САУ в среде Matlab, представленную на рис. 13, для случая передаточной функции в обратной цепи – позиционное звено Кос и передаточной функции в прямой цепи – интегрирующее звено с коэффициентом передачи Кпр – табл. 6.
2. Представить ММ в виде Transfer Fcn, Gain и Sum.
3. В области Simulink среды Matlab использовать окно
Tools |
и вызвать строку Linear analysis. |
|
|
|
|
||||||
|
4. Установить в среде Matlab |
на входе структурной |
|||||||||
схемы |
|
порт Iu и на выходе – Out. |
|
|
|
|
|
||||
|
5. Запустить |
процесс |
моделирования по набранной схе- |
||||||||
ме, нажав левой клавишей мышки на значок ►. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Таблица 4 |
||
|
|
|
Параметры передаточной функции САУ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
Колебательное звено |
ЖООС |
ГООС |
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кпр |
|
Тпр |
ξпр |
Кос1 |
Кос2 |
|
Тос |
|
|
1 |
|
12 |
|
0.112 |
0.52 |
1 |
2 |
|
0.022 |
|
|
2 |
|
14 |
|
0.114 |
0.54 |
1 |
4 |
|
0.022 |
|
24
Окончание табл. 4
3 |
16 |
0.116 |
0.56 |
1 |
6 |
0.022 |
4 |
18 |
0.118 |
0.58 |
1 |
8 |
0.022 |
5 |
20 |
0.120 |
0.60 |
1 |
10 |
0.033 |
6 |
22 |
0.122 |
0.62 |
1 |
2 |
0.033 |
7 |
24 |
0.124 |
0.64 |
1 |
4 |
0.033 |
8 |
26 |
0.126 |
0.66 |
1 |
6 |
0.033 |
9 |
28 |
0.128 |
0.68 |
1 |
8 |
0.011 |
10 |
30 |
0.130 |
0.70 |
1 |
10 |
0.011 |
11 |
32 |
0.132 |
0.72 |
1 |
2 |
0.011 |
12 |
34 |
0.134 |
0.74 |
1 |
4 |
0.011 |
13 |
46 |
0.136 |
0.76 |
1 |
6 |
0.044 |
14 |
48 |
0.138 |
0.78 |
1 |
8 |
0.044 |
15 |
50 |
0.140 |
0.80 |
1 |
10 |
0.044 |
6. Снять логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ) разомкнутой и замкнутой структурных схем, амплитудно-фазовую частотную характеристику (АФЧХ) разомкнутой структурной схемы и временные (переходную и импульсно-переходную) характеристики замкнутой структурной схемы в LTI View, вызвав правой клавишей мышки меню Plot tupe (для исследования в среде Matlab).
7. Повторить п. (3 – 6) для случая передаточной функции
впрямой цепи – апериодическое звено и в обратной – позиционное звено.
8.Повторить п. (3 – 6) для случая передаточной функции
впрямой цепи – колебательное звено и в обратной – позиционное звено Кос=Кос1.
9.Повторить п. 8 для того же колебательного звена в прямой цепи при ГООС в обратной цепи – реальное дифференцирующее звено с Кос=Кос2, постоянной времени Тос. Снять временные (ПХ и ИПХ) характеристики замкнутой структурной схемы.
25
10. Повторить п. (3 – 5) и снять только ПХ и ИПХ. 11. Сделать выводы по работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Виды соединений элементов в структурной схеме.
2.Правила переноса элементов в структурной схеме
3. Передаточная функция системы с отрицательной обратной связью (ООС) и положительной обратной связью
(ПОС).
4.Передаточная функция системы с гибкой отрицательной обратной связью (ГООС) и жесткой отрицательной обратной связью (ЖООС).
5.Логарифмические частотные характеристики (ЛЧХ) замкнутой и разомкнутой САУ с ООС.
6.Переходная и импульсная переходная характеристика САУ с ЖООС и ГООС.
7.Влияние ГООС на параметры качества регулирования.
ЛАБОРАТОРНАЯ РАБОТА № 4
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ОДНОКОНТУРНОЙ САУ
Цель работы: исследование одноконтурной САУ частотными и алгебраическими критериями устойчивости.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Устойчивость – это способность САУ, например, следящей системы (СС), при внешних воздействиях занимать устойчивое положение.
Алгебраические критерии устойчивости основаны на использовании характеристического уравнения системы. Харак-
26
теристическим уравнением является знаменатель передаточной функции замкнутой системы.
При корневом методе анализа устойчивости используется расположение корней на комплексной плоскости.
К частотным критериям устойчивости относится критерий Найквиста, который используется при анализе ампли- тудно-фазовой частотной характеристики (АФЧХ) и логарифмических амплитудной и фазовой частотных характеристик (ЛАЧХ и ЛФЧХ) разомкнутой системы.
По ЛАЧХ, ЛФЧХ и АФЧХ разомкнутой системы вво-
дятся понятия запаса устойчивости по фазе Δφ и запаса устойчивости по амплитуде L.
Устойчивость определяется и по виду ЛАЧХ и ЛФЧХ замкнутой системы.
Устойчивость определяется по виду переходной характеристики системы. При отсутствии колебаний или присутствии затухающих колебаний переходной характеристики или импульсной переходной характеристики система устойчивая. При наличии незатухающих колебаний по переходной характеристике система находится на границе устойчивости, а возрастающих колебаний – система неустойчивая.
ПРЕДВАРИТЕЛЬНОЕ ЗАДАНИЕ
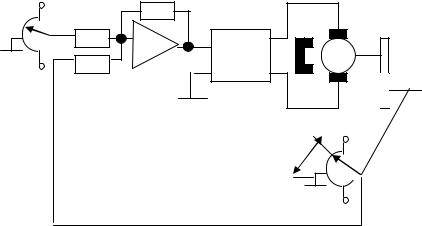
1.Рассчитать параметры ПФ элементов электромеханической следящей системы СС (см. табл. 5-6), приведенной на рис. 16. Выходной сигнал датчика обратной связи ДОС Uос = ±15 В при угле поворота его вала соответственно ± 180 градусов относительно исходного положения 0 градусов.
2.Представить структурную схему СС с единичной отрицательной обратной связью.
27
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
1. Задать структурную схему СС с единичной отрицательной обратной связью в подсистеме Simulink среды Matlab, используя функциональную схему на рис. 16.
1.1. В области Simulink использовать окно Tools и вы-
звать строку Linear analysis.
1.2. Вывести требуемые временные и частотные в LTI View, вызвав правой клавишей мышки меню Plot tupe.
2.Вывести комплексную плоскость распределения корней характеристического уравнения замкнутой системы.
Определить влияние коэффициента передачи разомкнутой системы на значение и расположение корней на плоскости, изменяя заданное значение коэффициента передачи предварительного усилителя Кпу (задаются дополнительно значения 2*Кпу и ½*Кпу).
3.Вывести частотные характеристики.
Выводится логарифмические амплитудная и фазовая частотные характеристики замкнутой системы с ООС и, при отключении ООС, выводится ЛАЧХ и ЛФЧХ разомкнутой системы. Определить запасы по фазе и амплитуде L по ЛЧХ разомкнутой системы. Получить зависимость запаса по фазе от коэффициента передачи разомкнутой системы, изменяя коэффициент передачи предварительного усилителя Кпу не менее (5 – 7) раз.
28
|
ПУ |
|
ЗУ |
Rос |
Д |
+Uп αз R1 |
УМ |
Р |
|
|
ωдв |
|
Uя |
Z1 |
-Uп |
Uп |
|
R2 |
|
|
|
|
Z2 |
αр
αр
ДОС
Uос
Рис. 16. Электромеханическая следящая система:
ЗУ – задающее устройство; ПУ – предварительный усилитель; УМ – усилитель мощности;
Д – двигатель постоянного тока; Р – редуктор; ДОС – датчик обратной связи;
αз – заданный угол поворота вала редуктора [рад.];
Uз – напряжение на выходе задающего устройства [В]; Uп – напряжение на выходе предварительного усили-
теля [В];
Uя – напряжение в якорной цепи [В];
αр – угол поворота выходного вала редуктора [рад.]; Z1, Z2 – число зубьев шестерен редуктора.
29
Таблица 5 Параметры элементов системы управления
вариант |
Предварительный |
Усилитель |
Редуктор |
||||
Усилитель |
|
мощности |
|
|
|||
R1,R2 |
Rос |
K |
|
T |
Z1 |
Z2 |
|
МОм |
МОм |
|
|
сек. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
0.5 |
2.0 |
15 |
|
0.001 |
24 |
48 |
2 |
0.5 |
2.0 |
15 |
|
0.002 |
24 |
48 |
3 |
0.5 |
2.0 |
15 |
|
0.003 |
24 |
48 |
4 |
0.5 |
2.0 |
15 |
|
0.004 |
24 |
48 |
5 |
0.5 |
2.0 |
15 |
|
0.005 |
24 |
48 |
6 |
1 |
2.0 |
35 |
|
0.001 |
24 |
60 |
7 |
1 |
2.0 |
35 |
|
0.002 |
24 |
60 |
8 |
1 |
2.0 |
35 |
|
0.003 |
24 |
60 |
9 |
1 |
2.0 |
35 |
|
0.004 |
24 |
60 |
10 |
1 |
2.0 |
35 |
|
0.005 |
24 |
60 |
11 |
1 |
2.0 |
15 |
|
0.001 |
24 |
96 |
12 |
1 |
2.0 |
15 |
|
0.002 |
24 |
96 |
13 |
1 |
2.0 |
15 |
|
0.003 |
24 |
96 |
14 |
1 |
2.0 |
15 |
|
0.004 |
24 |
96 |
15 |
1 |
2.0 |
15 |
|
0.005 |
24 |
96 |
4. Вывести амплитудно-фазовую частотную характеристику (АФЧХ) разомкнутой системы – nyquist.
Определить запас устойчивости по фазе для заданного коэффициента передачи разомкнутой системы (Кпу). Определить влияние изменения Кпу на вид АФЧХ разомкнутой системы.
5. Вывести поочередно переходную и импульсную переходную характеристики замкнутой системы – Step и Impulse.
Определить устойчивость системы по виду переходной
иимпульсно-переходной характеристик.
6.Сделать выводы по работе.
30
