
Теория автоматического управления. Лабораторный практикум в среде Matlab. учебное пособие. Харченко А.П., Слепокуров Ю.С
.pdf
Используя уравнения Кирхгофа для электрических цепей и уравнения моментов для электромеханических цепей для ДПТ, запишем систему уравнений:
|
|
|
|
|
|
di |
|
||
U н (t) iя (t) Rя |
L |
|
|
E(t) |
|||||
dt |
|||||||||
|
|
|
|
|
|
|
|||
|
(t) M н (t) M c (t) |
|
|||||||
M |
д |
|
|||||||
|
|
|
d (t) |
|
|
|
|
||
M |
|
(t) Jн |
|
|
|
|
|||
н |
|
|
|
|
|||||
|
|
dt |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
Всоответствии с принятыми обозначениями входа X(t)
ивыхода Y(t), необходимо получить уравнение, где вход – напряжение Uн(t), а выход – угловая скорость ω (t). Принимаем значение момента нагрузки Мс = 0.
Значение э.д.с. E(t) и значение электромагнитного номинального момента Мн(t) определяется из выражений:
E(t) Ce (t)M н (t ) См iя (t)
где См, Се – электромеханическая и электрическая постоянные Из уравнения моментов определяем значение тока
iя (t) Jн d . Cм dt
Записываем окончательное уравнение по закону Кирхгофа при замене в нем значения полученного тока iя(t), дополнительно поделив его слагаемые на величину Се и добавив в числитель и знаменатель при производной d²ω(t)/dt² значение сопротивления Rя
1 |
U |
(t) |
Jн Lя Rя |
|
d 2(t) |
|
J Rя |
|
d(t) |
(t). |
|
|
|
|
|
2 |
|
|
|||||
|
н |
|
CмСе Rя dt |
|
CмСе dt |
||||||
Се |
|
|
|
||||||||
Запишем предыдущее уравнение в операторной форме, произведя замену р = d/dt.
11
Вводим обозначения электромеханической постоянной времени Тм = JнRя/(СмСе), электромагнитной постоянной времени Тя = Lя/Rя и коэффициента передачи Кд = 1/Се.
Тм*Тя*р²*Y(p) + Тм*р*Y(p) + Y(p) = Кд*X(p).
Передаточная функция ДПТ определяется
W(p) = Кд/( Тм*Тя*р² + Тм*р + 1).
где Kд – коэффициент передачи; Tм,Tя – электромеханическая и электромагнитная постоянные времени.
Введенные постоянные коэффициенты определяются по формулам
Константа
См = Мн/Iя ,
где Мн – номинальный момент двигателя; Iя – номинальный ток двигателя.
Константа
Се = (Uн – Iя*Rя)* 30/(π*nн),
где nн – номинальная частота вращения вала двигателя;
При этом электромеханическая постоянная времени Тм ДПТ пропорциональна моменту инерции Jн и определяет его механическую инерционность. Чем больше электромеханическая постоянная времени Тм, тем медленнее разгоняется двигатель.
Если инерционность двигателя достаточно велика, т.е. механическая постоянная времени двигателя намного больше электромагнитной постоянной, то можно принять значение Тя = 0, тогда уравнение ДПТ определяется по формуле:
Тм*р*Y(p) + Y(p) = Кд*X(p).
12
Передаточная функция определяется, как апериодическое звено
W(p) = Кд/( Тм*р + 1).
Передаточная функция ДПТ по управляющему воздействию сводится к типовым звеньям второго порядка.
При Тм ‹ 4Тя – к колебательному звену с передаточной функцией:
W(s) = К / (Т² s² + 2 ξoТ s + 1),
где Т = √ТмТя – постоянная времени; ξo = 1/2√Тм/Тя – коэффициент демпфирования; К = Кд – коэффициент передачи.
При Тм ≥4Тя – к апериодическому второго порядка
звену
W(s) = К / (Т3*Т4 s² + (Т3+Т4) s + 1),
где Т3*Т4 = Тм*Тя , (Т3+Т4) = Тм – постоянные времени.
При решении дифференциального уравнения для двигателя малой мощности и подстановке Х(t) = 1(t), получим переходную функцию А звена:
h(t) = К*(1 – e-t/T).
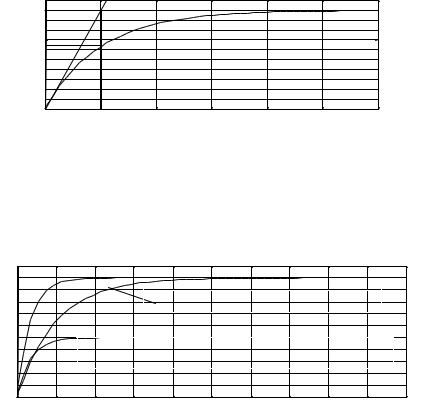
Переходная характеристика двигателя, как апериодического типового звена 1-го порядка представлена на рис. 6.
По переходной характеристике можно определить постоянную времени Т и коэффициент передачи К. Коэффициент передачи К равен установившемуся значению hуст.
Постоянная времени Т равна значению времени, соответствующему точке пересечения касательной к характеристике в начале координат с ее установившемся значением.
13
K |
hуст |
0.63K |
|
|
T |
Рис. 6. |
Переходная характеристика двигателя |
как апериодического звена 1-го порядка |
|
На рис. 7 приведены переходные характеристики при увеличении постоянной времени Т и уменьшении коэффициента передачи К двигателя.
Увеличение постоянной времени T |
|
Уменьшение коэффициента передачи двигателя К |
|
0 |
|
Рис. 7 |
t |
|
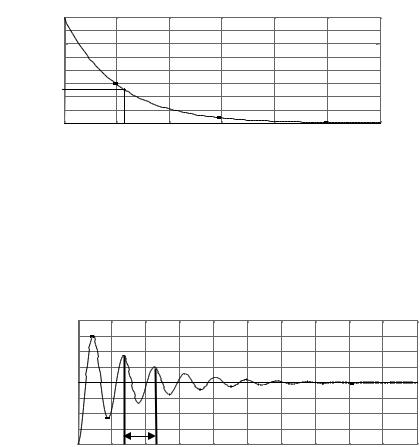
Постоянная времени влияет на длительность переходного процесса, а коэффициент передачи – на установившееся значение. Для апериодического звена 1-го порядка импульсная переходная характеристика определяется, как экспонента исходящая из точки К/Т и направленная вниз (рис. 8).
w(t) = dh(t)/dt = k/T*e.-t/T
14
К/Т |
|
|
0.37К/Т |
|
|
0 |
T |
t |
|
Рис. 8 |
|
|
|
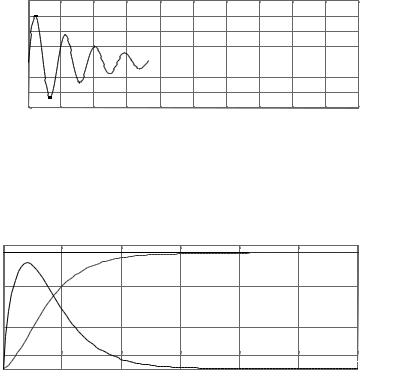
Переходная характеристика h(t) двигателя, как колебательного звена (рис. 9) определяется из дифференциального уравнения.
h(t) = K·[1 - e-αt sin (β t +φ],
где s1=-α-j β, s2=-α+j β – комплексные корни уравнения звена.
K
T=2π /β
0
Рис. 9. Переходная характеристика двигателя как колебательного звена
Из переходной характеристики можно определить параметры передаточной функции.
Коэффициент К определяется как установившееся значение переходной функции.
Зная период колебаний (Т = 2π/β) находим значения постоянной времени Т.
Импульсная переходная характеристика определяется:
15
w(t) = dh(t)/dt = |
k |
e t sin( t ). |
|
|
|||
T 2 |
|||
|
|
Импульсная переходная характеристика представлена на рис. 10.
0  t
t
Рис. 10. Импульсная переходная характеристика
Переходная характеристика и импульсная переходная характеристика двигателя, как апериодического 2-го порядка типового звена представлена на рис. 11.
w(t) h(t)
0 |
t |
|
Рис. 11. Переходная и импульсная переходная характеристики двигателя, как апериодического 2-го порядка звена
ПРЕДВАРИТЕЛЬНОЕ ЗАДАНИЕ
1. Рассчитать параметры передаточных функций на основании данных, приведенных для двигателей в табл. 2.
16
2.Значение сопротивления якорной обмотки Rя1 использовать для передаточной функции колебательного звена,
азначение сопротивления Rя2 – апериодического звена 2-го порядка.
3.Определить значения коэффициента передачи Кд констант См и Се, электромагнитной постоянной времени Тя и электромеханической постоянной времени Тм.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
1. Исследование ДПТ в библиотеке электронных эле-
ментов SimPowerSystems среды Matlab.
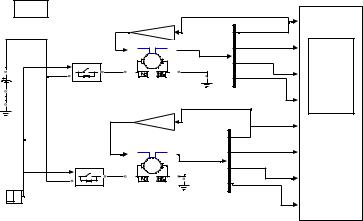
Схема моделирования двигателя без обмотки возбуждения представлена на рис. 12. Параметры двигателя для сопротивления Rя1 введены в верхнюю схему, а параметры двигателя для сопротивления Rя2 – в нижнюю схему.
Таблица 2
Технические данные двигателей
вариант |
вращенияЧастота n |
Напряжение В,Uн |
якоряТок А,Iя |
Сопротивление |
R |
Момент мН,Мн |
нерцииМомент 0,0001х²мКг,Jн |
Индуктивность Гн,Lя |
|
. |
|
|
|
Ом |
|
|
|
|
мин |
|
|
|
2я , |
|
|
|
|
об./ |
|
|
|
/R |
|
|
|
|
н |
|
|
|
я1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3000 |
60 |
2.86 |
0.46/1.0 |
0.39 |
15.3 |
0.004 |
|
2 |
2000 |
60 |
2.27 |
0.94/2.0 |
0.49 |
15.3 |
0.007 |
|
3 |
3000 |
110 |
1.53 |
1.48/3.0 |
0.39 |
15.3 |
0.012 |
|
4 |
2000 |
110 |
1.22 |
3.0/7.0 |
0.49 |
15.3 |
0.018 |
|
5 |
3000 |
60 |
4.57 |
0.23/0.5 |
0.65 |
20.4 |
0.0014 |
|
6 |
2000 |
110 |
2.72 |
0.52/1.0 |
0.585 |
20.4 |
0.0016 |
|
7 |
3000 |
60 |
2.46 |
0.765/1.5 |
0.65 |
20.4 |
0.0007 |
|
8 |
2000 |
110 |
1.46 |
1.74/3.5 |
0.585 |
20.4 |
0.0008 |
|
17
Окончание табл. 2
9 |
3000 |
60 |
5.6 |
0.284/0.6 |
0.81 |
35.7 |
0.0028 |
10 |
2000 |
110 |
4.3 |
0.645/1.4 |
0.97 |
35.7 |
0.0035 |
11 |
3000 |
60 |
3.05 |
0.945/1.9 |
0.81 |
35.7 |
0.017 |
12 |
2000 |
110 |
2.33 |
2.2/4.5 |
0.97 |
35.7 |
0.022 |
13 |
3000 |
60 |
8.2 |
0.192/0.74 |
1.2 |
40.8 |
0.0145 |
14 |
2000 |
60 |
5.5 |
0.36/0.76 |
1.22 |
40.8 |
0.0025 |
15 |
1000 |
60 |
2.6 |
1.44/3.6 |
1.17 |
40.8 |
0.0096 |
2. Двигатель DC Machines выбран из каталога
Mahines. Выключатель Ideal Switch – из Power Electronics. DC Voltage – из Electrical Sources. Остальные элементы – из каталога Simulink.
2.1. Задать параметры двигателя DC:
–сопротивление Rя1 и Rя1;
–индуктивность Lя;
–момент инерции Jн;
–константа Се;
–константа См = N.
C ontinuous |
|
|
powe rgui |
|
Gain |
|
|
0.1877 |
|
TL |
m |
|
|
dc |
g |
|
|
2 |
A+ |
A- |
1 |
|
|
DC Voltage Source Ideal Switch |
DC Machine |
|
|
|
Gain1 |
|
|
0.2784 |
|
TL |
m |
|
|
dc |
g |
|
|
2 |
A+ |
A- |
1 |
|
|
Ideal Switch1 |
DC Machine1 |
|
Step
Scope
Рис. 12. Схема моделирования двигателя без обмотки возбуждения
18
2.2.Задать параметры напряжения – Uн.
2.3.Запустить расчет, нажав левой клавишей мышки на значок ►, и сравнить установившейся значения скорости вращения, тока и развиваемого момента схем для Rя1 и Rя2.
2.4.Исследовать влияние напряжения Uн и момента инерции Jн на форму и значения скорости.
3. Исследование двигателя в средах Matlab или Scilab.
Схема моделирования (структурная схема) двигателя постоянного тока представлена на рис. 13-14.
Якорная цепь двигателя (ЯЦД) описывается апериодическим звеном 1-го порядка с коэффициентом K = 1/Rя, механическая часть двигателя (МЧД) – интегрирующим звеном 1/(Jн*p) и две константы Се, См – пропорциональным звеном.
Управляющим воздействием является напряжение Uн, управляемым – угловая скорость вращения вала ДПТ ωвр, а возмущающим – момент нагрузки Мс (принимаем Мс = 0).
Представленные схемы моделирования двигателя посто-
янного тока (рис. 13 и рис. 14) |
позволяют анализировать |
||||||||||||||||
временные и частотные характеристики. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mc(p) |
|
ωвр(p) |
|
|
Uя(p) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
К/(Тя p+1) |
|
|
См |
|
|
|
|
1/(Jн p) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Cе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 13. Схема моделирования двигателя постоянного тока в среде Matlab
3.1. Задать схему моделирования двигателя постоянного тока как колебательного и апериодического 2-го порядка типовых звеньев, представленные на рис. 13 или рис. 14, задав константы К = 1/Rя1, Тя1 для случая Rя = Rя1 и К = 1/Rя2, Тя2 для случая Rя = Rя2.
19
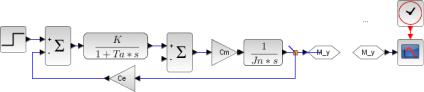
Рис. 14. Схема моделирования двигателя постоянного тока в среде Scilab
3.2. |
Для структурной схемы в среде Matlab установить |
||
на входе |
порт (элемент) |
In и на выходе – порты |
(элемен- |
ты) Out1Out2 из меню |
Sources и Sinks.). |
|
|
3.3. |
В области Simulink среды Matlab использовать окно |
||
Tools и вызвать строку Linear analysis. |
|
||
3.4. Вывести требуемые временные и частотные харак- |
|||
теристики в LTI View, вызвав меню Plot tupe. |
|
||
3.5. |
Снять контрольные точки переходной |
характе- |
|
ристики h(t=0), h(t=?)=hуст/2, h(t=∞) и импульсной переходной характеристики w(t =0 ), w(t = ?)=wмак/2 и w(t = ∞).
3.6.Снять контрольные точки частотных характеристик
–амплитудно-фазовой частотной характеристики АФЧХ и логарифмических частотных характеристик ЛЧХ.
3.7.Исследовать влияние изменения коэффициента К=1/Rя, постоянной времени Тя и момента инерции Jн на временные характеристики ДПТ.
4. Сделать выводы по работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как определить параметры временных характеристик апериодического звена и типового звена 2-го порядка?
3.Какими типовыми динамическими звеньями представляется двигатель постоянного тока и при каких условиях?
4.Как влияет коэффициент передачи К и постоянная времени Т на временные и частотные характеристики апериодического звена?
20
