
Теория автоматического управления. Лабораторный практикум в среде Matlab. учебное пособие. Харченко А.П., Слепокуров Ю.С
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВО «Воронежский государственный технический университет»
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
ЛАБОРАТОРНЫЙ ПРАКТИКУМ В СРЕДЕ MATLAB
Утверждено учебно-методическим советом университета в качестве учебного пособия
Воронеж 2018
УДК 681.51.01 (075.8)
ББК 33.97я7
Т338
Авторы:
А.П. Харченко, Ю.С. Слепокуров. О.В. Белоусова, И.Ю. Свирский
Рецензенты:
кафедра электроэнергетики Международного института компьютерных технологий (г. Воронеж)
(зав. кафедрой д-р техн. наук, проф. А.Н. Анненков); канд. техн. наук, доц. В.А. Трубецкой
Теория автоматического управления. Лабораторный практикум в среде Matlab: учеб. пособие [Текст] /
Т338 А.П. Харченко, Ю.С. Слепокуров. О.В. Белоусова, И.Ю. Свирский. – Воронеж: ФГБОУ ВО «Воронежский
государственный технический университет», 2018. – 106 с.
ISBN 978-5-7731-0631-9
Пособие включает вопросы анализа и синтеза динамических и статических показателей качества управления автоматических систем.
Учебное пособие составлено в соответствии с Федеральным государственным образовательным стандартом высшего образования по программе курсов «Теория автоматического управления» и «Управление в технических системах» и предназначено для студентов направления подготовки 13.03.02 «Электроэнергетика и электротехника», (профили «Электропривод и автоматика в робототехнических системах», «Электропривод и автоматика», «Электромеханика»).
Предназначено для студентов 3 курса.
Табл. 20. Ил. 43. Библиогр.: 5 назв.
УДК 681.51.01 (075.8)
ББК 33.97я7
ISBN 978-5-7731-0631-9 © Харченко А.П., Слепокуров Ю.С., Белоусова О.В., Свирский И.Ю.,
2018
©ФГБОУ ВО «Воронежский государственный технический университет», 2018
2
ВВЕДЕНИЕ
Теория автоматического управления (ТАУ) изучает свойства различных, в основном технических систем, с целью обеспечения наиболее благоприятных условий работы.
Одной из основных отличительных особенностей автоматических систем (АС) является выявление и практическое использование общих закономерностей, имеющихся в работе систем различной физической природы – механических, пневматических, гидравлических, электрических, электронных.
Синтез АС заключается в проектировании специальных устройств, которые должны обеспечивать выполнение возложенной задачи с желаемым качеством, двигаться по заданной траектории в пространстве и во времени.
В технической системе это регуляторы перемещения, регуляторы скорости, регуляторы напряжения, регуляторы тока и т.д.
Определение параметров регуляторов и корректирующих устройств базируется на использовании возможностей прикладных программ для математического описания в виде передаточных функций или дифференциального уравнения для получения заданного переходного процесса.
При проектировании технических систем предлагаются
современные методы анализа и синтеза |
систем автоматиче- |
ского управления путем компьютерного моделирования. |
|
Лабораторный практикум предназначается для практи- |
|
ческой проверки основных положений |
ТАУ, закрепления у |
студентов теоретических знаний, получения навыков работы с пакетом прикладных программ для моделирования непрерывных и дискретных систем в средах Matlab и Scilab.
3
ЛАБОРАТОРНАЯ РАБОТА № 1
ИССЛЕДОВАНИЕ ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
Цель работы: исследование частотных и временных характеристик типовых звеньев первого порядка.
ТЕРЕРЕТИЧЕСКИЕ СВЕДЕНИЯ
Математические модели (ММ) представляются в ча-
стотной и временной форме. |
При задании на входе системы |
или элемента гармонического сигнала вида Х(t) = Хm sin ωt, |
|
на выходе |
ММ |
так же появляется гармонический выход- |
ной сигнал |
той |
же частоты ω вида |
|
|
У(t) = Уm (sin ωt + φ). |
Отношение амплитуды выходного сигнала ММ к амплитуде входного сигнала называется амплитудной частотной характеристикой (АЧХ)
А(ω) =Уm(ω) / Хm(ω).
Если для АЧХ ось частот ω перевести в логарифмический масштаб lgω (десятичный логарифм ω), а ось А(ω) перевести в логарифмический масштаб L(ω), тогда получим логарифмическую частотную амплитудную характеристику
(ЛАЧХ) вида
L(ω) = 20lgA(ω).
Для типовых звеньев вводится понятие амплитуднофазовой частотной характеристики (АФЧХ) W(jω), если в ММ – передаточной функции W(s), провести замену переменной s на jω.
4
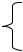
АФЧХ – это график частотной передаточной функции (ЧПФ), определяемой по формулам
W(jω) = U(ω) + jV(ω)
W(jω) = A(ω) ℮j φ(ω) ,
где U(ω), V(ω) – действительная (вещественная) и мнимая части ЧПФ; A(ω) – модуль вектора АФЧХ; φ(ω) – фазовая частотная характеристика.
Фазовая частотная характеристика (ФЧХ) φ(ω), определяется из координат модуля вектора A(ω)
φ (ω)=arctg V(ω) / U(ω).
Временные характеристики описывают реакцию системы или элемента на типовой входной сигнал.
При подаче на вход элемента или системы ступенчатой единичной функции х(t) = k*1(t) на выходе появляется переходная характеристика h(t).
При подаче на вход элемента или системы импульсного сигнала (дельта функция) х(t) = δ(t) на выходе появляется импульсная переходная характеристика w(t).
ПРЕДВАРИТЕЛЬНОЕ ЗАДАНИЕ
1.Записать дифференциальные уравнения элементов, приведенных на рис. 3 – 4, Параметры элементов представлены в табл. 1. Представить уравнения в операторной или операционной формах.
2.Определить передаточные функции элементов, как типовых динамических звеньев.
3.Вычисления коэффициентов передач К и постоянных времени Т проводить с точностью до 0.001.
5
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ
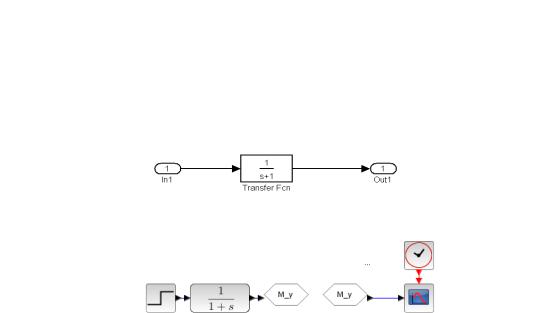
1.Задать схему моделирования элементов в среде Matlab
–рис. 1 или в среде Scilab – рис. 2.
1.1.Представить ММ в виде Transfer Fcn.
1.2.Установить на входе Transfer Fch порт In, на выхо-
де порт Out – среда Matlab или блоки Step, Out, Scope, Clock
–среда Scilab.
1.3.Для среды Matlab в области Simulink использовать окно Tools и вызвать строку Linear analysis.
Рис. 1. Схема моделирования элементов в среде Matlab
Рис. 2. Схема моделирования элементов в среде Scilab
2.Запустить процесс моделирования по набранной схе-
ме, нажав левой клавишей мышки на значок ►.
3.Снять частотные характеристики: амплитудную частотную характеристику АЧХ, логарифмическую амплитудную частотную характеристику ЛАЧХ и логарифмическую фазовую частотную характеристику ЛФЧХ, амплитудно-фазовую частотную характеристику АФЧХ и временные характеристики: переходную характеристику ПХ и импульсную переходную характеристику ИПХ типовых динамических звеньев.
4.Определить влияние коэффициента передачи К и постоянной времени Т на параметры частотных и временных характеристик.
5.Сделать выводы по работе.
6
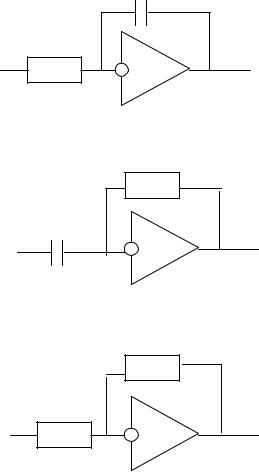
Сос
Rвх
а
Rос
Свх
б
R2
R1
в
Рис. 3. Схемы типовых звеньев: а – интегрирующее звено, б – дифференцирующее звено, в – усилительное звено
7
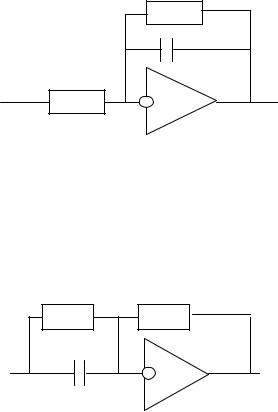
R4
R3 |
C1 |
|
а
R5 R6
C2
б
Рис. 4. Схемы типовых звеньев: а – апериодическое звено, б – форсирующее звено
8
Таблица 1
Параметры типовых звеньев
вариант |
Cвх |
Rос |
Rвх |
Сос |
R1 |
R2 |
C1 |
R3 |
R4 |
C2 |
R5 |
R6 |
мкФ |
МоМ |
МоМ |
мкФ |
МоМ |
МоМ |
мкФ |
МоМ |
МоМ |
мкФ |
МоМ |
МоМ |
|
1 |
1 |
1 |
1 |
0.1 |
1 |
0.1 |
0.01 |
1 |
1 |
0.1 |
1 |
0.1 |
2 |
2 |
1 |
1 |
0.2 |
1 |
0.2 |
0.02 |
1 |
2 |
0.2 |
1 |
0.2 |
3 |
3 |
1 |
1 |
0.3 |
1 |
0.3 |
0.03 |
1 |
1 |
0.3 |
1 |
0.3 |
4 |
4 |
1 |
1 |
0.4 |
1 |
0.4 |
0.04 |
1 |
2 |
0.4 |
1 |
0.4 |
5 |
5 |
1 |
1 |
0.5 |
1 |
0.5 |
0.05 |
1 |
1 |
0.5 |
1 |
0.5 |
6 |
6 |
1 |
1 |
0.6 |
1 |
0.6 |
0.06 |
1 |
2 |
0.6 |
1 |
0.6 |
7 |
7 |
1 |
1 |
0.7 |
1 |
0.7 |
0.07 |
1 |
1 |
0.7 |
1 |
0.7 |
8 |
8 |
1 |
1 |
0.8 |
1 |
0.8 |
0.08 |
1 |
2 |
0.8 |
1 |
0.8 |
9 |
9 |
1 |
1 |
0.9 |
1 |
0.9 |
0.09 |
1 |
1 |
0.9 |
1 |
0.9 |
10 |
10 |
1 |
1 |
1 |
1 |
1 |
0.1 |
1 |
2 |
1 |
1 |
1 |
11 |
0.1 |
1 |
1 |
2 |
1 |
2 |
0.001 |
1 |
1 |
0.01 |
1 |
2 |
12 |
0.2 |
1 |
1 |
3 |
1 |
3 |
0.002 |
1 |
2 |
0.02 |
1 |
3 |
13 |
0.3 |
1 |
1 |
4 |
1 |
4 |
0.003 |
1 |
1 |
0.03 |
1 |
4 |
14 |
0.4 |
1 |
1 |
5 |
1 |
5 |
0.004 |
1 |
2 |
0.04 |
1 |
5 |
15 |
0.5 |
1 |
1 |
6 |
1 |
6 |
0.005 |
1 |
1 |
0.05 |
1 |
6 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Классическая, операторная и операционная формы записи уравнений элементов.
2.tf -форма и zpk-форма математических моделей
3. Передаточная функция.
4. Частотная передаточная функция.
5. Переходная и импульсная переходная характеристики.
6. Амплитудная и фазовая частотные характеристики.
7. Логарифмические частотные характеристики.
9
ЛАБОРАТОРНАЯ РАБОТА № 2
ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА
Цель работы: исследование временных характеристик двигателя постоянного тока, как апериодического и типовых звеньев 2-го порядка при типовых входных сигналах.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Рассмотрим в качестве двигателя постоянного тока (ДПТ) – двигатель с возбуждением от постоянных магнитов.
Управление ДПТ осуществляется по одной цепи – цепи якорной обмотки с помощью подводимого напряжения от источника питания.
На рис. 5 представлены условное обозначение и схема замещения ДПТ с указанием скорости вращения ωвр(t), момента сопротивления Мс(t), сопротивления якорной обмотки
Rя, индуктивности Lя, мгновенного значения тока iя(t), наводимой э.д.с. E(t) и напряжения Uн(t).
|
|
|
|
|
|
|
|
|
|
Rя |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωвр(t) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
Uн(t) |
|
|
|
|
|
|
Uн(t) |
|
Iя(t) |
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Lя |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(t) |
||
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 5. Условное обозначение и схема замещения ДПТ |
|||||||||||||
10
