Учебное пособие 800378

сетевого типа, выражающиеся, например, в публикации совместных работ. Такая закономерность наблюдается также в других реальных сетях и отражает такую тенденцию, как хорошая связность между узлами-концентраторами. Это явление, известное под названием элитарность (или феномен

«клуба богатых» — rich-club phenomenon), может быть охарактеризовано коэффициентом элитарности, введенным в

работе [71]. Анализ топологии веб, проведенный Ши Жоу (S. Zhou) и Р. Дж. Мондрагоном (R.J. Mondragon) из Лондонского университета, показал, что узлы с большой степенью исходящих гиперссылок имеют больше связей между собой, чем с узлами с малой степенью, тогда как последние имеют больше связей с узлами с большой степенью, чем между собой. Исследование показало, что 27 % всех соединений имеют место между всего 5 % наибольших узлов, 60 % приходится на соединения других 95 % узлов с 5 % наибольших и только 13 %

— это соединения между узлами, которые не входят в лидирующие 5 %.

Элитарность степени k у сети G- это некое множество

где сумма соответствует удвоенному количеству ребер между вершинами в «элите». Эта характеристика подобна коэффициенту кластерности, она определяет долю связей, существующих между узлами со степенью, превышающей k .

1.2.9. Корреляция степеней связанных вершин

Значительное количество структурных и динамических свойств сети определяется с помощью оценки корреляции между степенями соседних узлов. Такая корреляция может

21

быть выражена через совокупное распределение P(k,k'), т.е. как вероятность того, что произвольно выбранное ребро соединяет узел степени k с узлом степени k'. Зависимость между степенями вершин можно выразить в терминах условной вероятности того, что произвольно выбранный сосед вершины

предшествующего узла, k' — степень последующего узла, значения k и k' могут быть входными, выходными или полными

экспериментальным путем, что связано с размером сети и малой мощностью выборки узлов с высокими степенями. Эту проблему можно решить, вычислив среднюю степень ближайших соседей узлов с заданной степенью k по формуле:

( ) = ( | ), (1.13)

Показатель корреляции степеней связности позволяет выделить отдельные классы сетей. Если корреляция отсутствует, то S(k) не зависит от значений k , ( ) = / . Если ( ) возрастает при увеличении k , то узлы больших степеней тяготеют к соединениям с узлами больших степеней, и сеть относят к ассортативным (отсюда и феномен «клуба богатых»), тогда как если ( ) — убывающая функция от k , то вершины больших степеней тяготеют к соединениям с вершинами малых степеней, и сеть называют дизассортативной

[68].

Известно, что ассортативные сети менее уязвимы к равновероятным атакам, а дизассортативные менее уязвимы к

22

целенаправленным атакам на узлы-концентраторы. Также, например, синхронизация состояния компонент сети происходит быстрее в ассортативных сетях. Например, при распространении заразной болезни социальные сети в идеальном случае должны быть ассортативны: при контроле малой доли узлов-концентраторов сеть разбивается на изолированные компоненты связности, что позволяет эффективно контролировать распространение инфекции.

23

2. ТОПОЛОГИЧЕСКИЕ МОДЕЛИ СЕТЕВЫХ СТРУКТУР

2.1. Графы, как модели сетевых структур

Тополо́гияструктур (от греч. τόπος, — место) — способ описания конфигурации сети, схема расположения и соединения устройств [23].

К основным типам топологий структур можно отнести: 1.Тип общая шина (рис. 2.1) позволяет значительно

упростить логическую и программную структуру сети.

Рис. 2.1. Топология шина

2. Древовидная топология (рис.2.2) представляет собой более развитый вариант конфигурации типа общая шина. Дерево образуется путем соединения нескольких шин активными повторителями или сетевыми концентраторами. При наличии активных повторителей отказ одного сегмента не приводит к выходу из строя остальных. В случае отказа повторителя дерево разделяется на два поддерева или на две шины [23].

Рис. 2.2. Древовидная топология

24

3. Развитием конфигурации типа дерево является сеть типа звезда (рис.2.3), которую можно рассматривать как дерево, имеющее корень с ответвлениями к каждому подключенному устройству. В центре звезды может находиться пассивный соединитель или хаб - достаточно простые и надежные устройства. Звездообразные структуры менее надежны, чем шина или дерево [23].

Рис. 2.3. Топология "звезда"

4. При произвольном соединении (рис.2.4) все устройства соединены непосредственно. Каждая линия может использовать в себе различные методы передачи. Такой способ соединения устройств вполне удовлетворителен для структур с ограниченным числом соединений. Преимущество данного типа - простота. Однако он имеет высокую стоимость, большое число каналов связи и необходимость маршрутизации информации [23].

Рис. 2.4. Произвольное соединение

25

5. В иерархическом соединении (рис.2.5) промежуточные узлы работают по принципу: “накопи и передай”. Преимущества данного метода - оптимальное соединение элементов сети. Недостатки - сложность логической и программной структуры, различная скорость передачи информации на различных уровнях [23].

Рис. 2.5.Иерархичное соединение

6. В конфигурациях кольцо, цепочка, звезда с “интеллектуальным” центром, снежинка (рис.2.6) для правильного функционирования сети необходима постоянная работа всех блоков. Чтобы уменьшить эту зависимость в каждый блок включают реле, блокирующее блок при неисправностях. Для упрощения сигналы передаются по кольцу только в одном направлении. Недостатки - замедленная передача данных (в зависимости от числа рабочих станций), меньшая надежность. Достоинства - простота методов управления, высокая пропускная способность при меньших энергозатратах, простота расширения структуры [23].

26

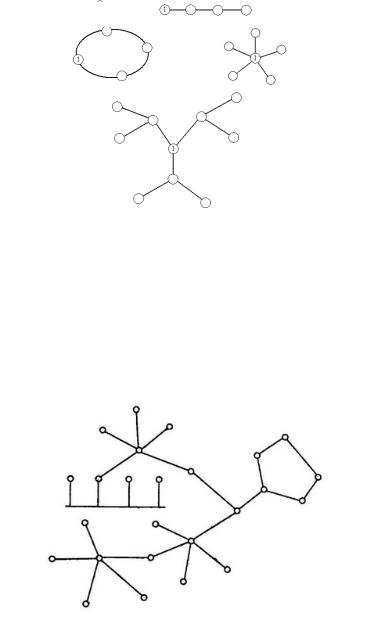
Рис. 2.6. Конфигурация кольцо, цепочка, звезда с “интеллектуальным” центром, снежинка

7. Гибридная топология. Гибридные топологии комбинируют топологии звезда, шина, кольцо. Это наиболее часто реально используемая топология. Гибридные топологии наиболее распространенные в современных системах передачи данных [23].

Рис. 2.7. Гибридная топология

27

2.2. Случайные графы 2.2.1. Основное понятие

Случайный граф — это общий термин для обозначения вероятностного распределения графов. Случайные графы можно описать просто распределением вероятности или случайным процессом, создающим эти графы. Теория случайных графов находится на стыке теории графов и теории вероятностей. С математической точки зрения случайные графы необходимы для ответа на вопрос о свойствах типичных графов. Случайные графы нашли практическое применение во всех областях, где нужно смоделировать сложные сети — известно большое число случайных моделей графов, отражающих разнообразные типы сложных сетей в различных областях. В математическом контексте термин случайный граф означает почти всегда модель случайных графов Эрдёша– Реньи. В других контекстах любая модель графов означает случайный граф[58].

Теория случайных графов изучает типичные свойства случайных графов, которые выполняются с большой степенью вероятности для графов, полученных для определённого распределения. Например, мы можем спросить для заданных значений n и p, какова вероятность, что G(n,p) связен. При изучении таких вопросов исследователи часто концентрируются на асимптотическом поведении случайных графов — значениях, к которым стремятся различные вероятности при росте n. Теория перколяции описывает связность случайных графов, в особенности неограниченно больших[58].

Перколяция связана с устойчивостью графа (называемого также сетью). Пусть дан случайный граф с n вершинами и средней степенью <k>. Удалим случайную 1−p часть рёбер и оставим p часть. Существует критический порог перкуляции

28

ниже которой сеть становится фрагментированной, в то время как выше pc существуют огромные компоненты связности.[66]

Случайные графы широко используются в вероятностном методе, когда пытаются доказать существование графов с определёнными свойствами. Существование свойства на случайных графах могут часто иметь следствием, по лемме регулярности Семереди, существование этого свойства почти для всех графов[64].

Для случайных регулярных графов G(n,r-reg) — это множество r-регулярных графов с r=r(n), таких что n и m — натуральные числа, 3 ≤r<n, и rn= 2m чётно.

Последовательность степеней графа G в Gn зависит только от числа рёбер в множествах

Vn(2) = {ij: 1≤ j ≤ n, i ≠ j} ϲ V(2), i = 1, …, n, (2.2)

Если множество рёбер M в случайном графе GM достаточно большое, чтобы почти все GM имели минимальную степень не меньше 1, то почти любой GM связен и, для чётного n, почти любой GM содержит совершенное паросочетание. В частности, в момент, когда исчезает последняя изолированная вершина почти во всех случайных графах, граф становится связным.[59]

Почти любой процесс построения графа с чётным числом вершин при достижении минимальной степени 1 или случайного графа при достижении чуть больше чем (n/4)log(n) рёбер с вероятностью, близкой к 1 обеспечивает существование полного паросочетания, за исключением, может быть, одной вершины.

Для некоторой константы c почти каждый помеченный граф с n вершинами и как минимум cnlog(n) рёбрами является гамильтоновым. С вероятностью, стремящейся к 1, добавление ребра, увеличивающее минимальную степень графа до 2, делает его гамильтоновым.

29

2.2.2. Основные модели теории случайных графов

Рассмотрим основные модели теории случайных графов.

1)Модель Эрдеша – Реньи.[27]

На рубеже 50ых и 60ых годов ХХ века эту модель предложили классики современной комбинаторики и теории вероятностей П. Эрдеш и А. Реньи. Эрдеш – это, пожалуй, одна из самых ярких фигур в математике ХХ века. Ему принадлежат сотни статей и задач, которые оказали огромное влияние на развитие многих математических дисциплин. Реньи также сыграл значительную роль в формировании венгерской вероятностной школы, и его именем назван математический институт в Будапеште.

Пусть дано множество Vn={1,...,n},элементы которого мы назовем вершинами. Именно на этом множестве мы будем«строить» случайный граф. Понятно, что случайным будет множество ребер графа. Потенциальных ребер у графа не больше, чем Cn2 штук. Будем соединять любые две вершины i и j ребром с некоторой вероятностью p [0,1]независимо от всех остальных Cn2−1 пар вершин. Иными словами, ребра появляются в соответствии со стандартной схемой Бернулли, в которой Cn2 испытаний и «вероятность успеха» p. Обозначим через E случайное множество ребер, которое возникает в результате реализации такой схемы. Положим G=(Vn, E). Это и есть случайный граф в модели Эрдеша – Реньи.

Если записывать приведенное только что определение в формате аксиоматики Колмогорова, то мы имеем вероятностное пространство:

где Ωn={G=(Vn,E)}, Fn=2Ωn, Pn,p(G)=p|E|(1−p)^(Cn2-|E|).

30