
Теплотехника. Учебное пособие. Мозговой Н.В., Бараков А.В
.pdf
q
q
q
|
|
t1 |
t2 |
; |
|
||
1 |
|
||||||
|
|
|
|
|
|
|
|
1 |
|
t |
|
t |
|
; |
(2.14) |
|
|
2 |
3 |
||||
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
3 |
|
t |
|
t |
|
. |
|
|
|
3 |
4 |
|
|||
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
Из (2.14) находим значения температурных напоров для каждого слоя стенки
t1 |
t2 |
q |
t2 |
t3 |
q |
t3 |
t4 |
q |
1
1
2
2
3
3
Сложение левых и правых частей дает
t1 t4 |
|
q |
|
1 |
|
|
2 |
|
|
3 |
. |
||||||||
|
1 |
|
2 |
|
|
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Отсюда тепловой поток |
|
|
|||||||||||||||||
q |
|
|
|
t1 |
|
|
t4 |
|
|
|
|
|
|
(2.15) |
|||||
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
||
По аналогии для n – слойной стенки |
|||||||||||||||||||
q |
t1 |
tn |
1 |
|
|
|
|
|
|
|
|
|
|
(2.16) |
|||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Внутри каждого слоя плоской многослойной стенки температура изменяется по закону прямой, в целом для многослойной стенки температурный профиль выразится ломаной линией.
71
t
|
|
dx |
|
t1 |
|
|
|
Q |
|
|
|
r1 |
|
|
l |
|
|
|
t2 |
r2 |
δ1 |
δ2 |
δ3 |
|
|
Рис. 41 |
x |
|
|
|
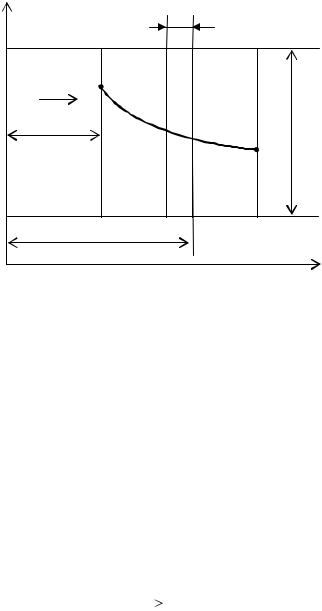
2.1.6. Теплопроводность однослойной цилиндрической стенки.
Довольно часто теплоносители движутся по трубам и требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы. Задача о тепловом переносе в цилиндрической стенке при известных и постоянных температурах на внутренней и наружной поверхностях одномерная, поэтому температура изменяется только вдоль радиуса, а по длине трубы и по ее периметру остается неизменной.
Имеем цилиндрическую стенку или трубу длиной l с внутренним радиусом r1 и наружным r2 . Коэффициент теплопроводности материала стенки равен  и не зависит от температуры. На внутренней поверхности стенки поддерживается температура t1 и на наружной t2 (при этом t1 t2 ). Выделим в стенке на расстоянии
и не зависит от температуры. На внутренней поверхности стенки поддерживается температура t1 и на наружной t2 (при этом t1 t2 ). Выделим в стенке на расстоянии
r от оси трубы кольцевой слой материала толщиной dr . В этом случае закон Фурье имеет вид
72
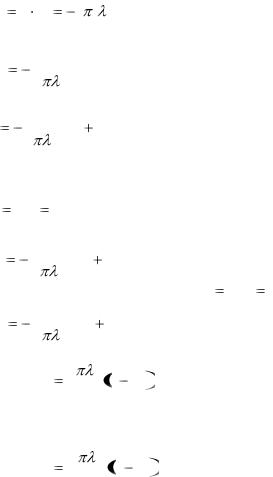
Q q |
F |
|
|
|
|
2 r l |
dt |
. |
|
(2.17) |
|||||||||||||
|
|
dr |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разделим переменные |
|
|
|
|
|||||||||||||||||||
dt |
|
|
|
Q |
|
|
|
|
dr |
. |
|
|
|
|
|
|
|
|
|
(2.18) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
l r |
|
|
|
|
|
|
|
|
|
|
|||||||
Интеграл уравнения (2.18) |
|
||||||||||||||||||||||
t |
|
|
|
|
Q |
ln r |
C |
|
|
|
(2.19) |
||||||||||||
|
2 |
l |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
показывает, что распределение температуры по радиусу |
|||||||||||||||||||||||
стенки подчиняется логарифмическому закону. |
|
||||||||||||||||||||||
При первом граничном условии |
|
||||||||||||||||||||||
r r1 ,t t1 , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
уравнение (2.19) принимает вид |
|
||||||||||||||||||||||
t |
|
|
|
|
Q |
|
|
ln r |
|
|
|
|
C |
|
|
|
(2.20) |
||||||
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
l |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и при втором граничном условии r r2 , t |
t2 |
||||||||||||||||||||||
t |
|
|
|
|
Q |
|
|
ln r |
|
|
|
|
C . |
|
|
|
(2.21) |
||||||
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
l |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вычитая из (2.20) (2.21), получаем |
|
||||||||||||||||||||||
|
|
|
|
|
Q |
|
|
2 |
|
|
|
l |
|
|
t |
t |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ln |
|
r2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.22) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 |
|
|
|
|||||||
или заменяя радиусы на диаметры получаем |
|
||||||||||||||||||||||
|
|
|
|
|
Q |
|
|
2 |
|
|
|
l |
t |
t |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
ln |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
d1 |
|
|
|
|
|
(2.23) |
|||||||
Из (2.22) и (2.23) видно, что тепловой поток через цилиндрическую стенку прямо пропорционален коэффициенту теплопроводности материала стенки, еѐ длине и падению температуры в стенке и обратно пропорционален натуральному логарифму отношения диаметров или радиусов стенки.
73
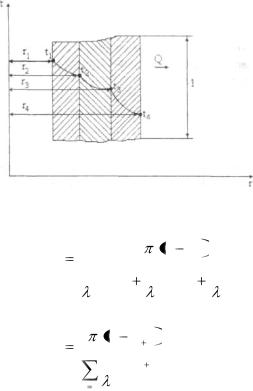
2.1.7. Теплопроводность многослойной цилиндрической стенки
Для определения теплового потока через многослойную цилиндрическую стенку следует, как и для многослойной плоской стенки, просуммировать термические сопротивления отдельных слоев.
Рассмотрим цилиндрическую стенку, состоящую из трех
слоев.
|
|
Рис. 42 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
2 l t1 |
t4 |
|
|
|
|
|
||||||
1 |
ln |
r2 |
|
|
1 |
|
ln |
r3 |
|
1 |
ln |
r4 |
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
2 |
r2 |
3 |
r3 |
(2.24) |
||||||||
|
|
|
|
|
r1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для n – слойной стенки |
|
|
|
|
|
|
|
||||||||||||
Q |
|
2 l t1 |
|
tn |
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
n |
1 |
|
|
|
r |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
ln |
l |
|
|
|
|
|
|
|
|
|
|
||
|
|
l 1 |
1 |
r1 |
|
|
|
|
|
(2.25) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Неизвестные температуры на границах раздела слоев можно найти, применяя для каждого слоя уравнение (2.23) предыдущего параграфа, в котором значение Q подставляется из формулы (2.25).
74
2.2. Конвективный теплообмен (теплоотдача)
2.2.1. Основной закон конвективного теплообмена
Конвективным теплообменом или теплоотдачей называется процесс теплообмена между твѐрдым телом и омывающей его жидкостью, осуществляемый одновременно действием теплопроводности и конвекции в жидкости. Здесь под жидкостями понимаются как жидкости в обычном их понимании, так и газы.
Q
жидкость
Рис. 43
Согласно закону Ньютона - Рихмана тепловой поток Q в процессе теплоотдачи пропорционален площади поверхности теп-
лообмена F и разности температур поверхности tC |
и жидкости tж : |
|
Q |
F tc tж |
(2.26) |
|
|
|
Здесь коэффициент пропорциональности |
называется ко- |
|
эффициентом теплоотдачи; его единица измерения Вт/м 2 К. Он характеризует интенсивность процесса теплоотдачи. Численное значение его равно тепловому потоку от единичной поверхности теплообмена при разности температур поверхности и жидкости в один градус.
Формула Ньютона - Рихмана является удобной для расчетов в практических задачах. Наиболее трудно определяемой величиной в ней является коэффициент теплоотдачи , который зависит от большого числа переменных.
f l, ,C pФ, v,.... |
(2.27) |
|
75

2.2.2. Основные факторы, влияющие на теплоотдачу
Анализ показывает, что количество теплоты, передаваемой при конвективном теплообмене, в наибольшей степени зависит от физических свойств жидкости, интенсивности движения еѐ, температурных условий, при которых осуществляется теплообмен, и геометрической формы и размеров теплообменной поверхности.
1. Физические свойства жидкости На теплообмен особенно заметно влияют теплофизические и
гидродинамические свойства жидкости. Теплофизические свойства жидкости описываются коэффициентом температуропроводности a и гидродинамические свойства - коэффициентом кинематической вязкости жидкости v. Обобщѐнной характеристикой физических свойств жидкости, влияющих на теплоотдачу, является безразмерный комплекс из указанных величин.
v
Pr a (2.28)
Комплекс (2.28), имеющий безразмерный вид, называется критерием, или числом Прандтля.
2 Интенсивность движения жидкости Различают два рода движения жидкости, а именно: свобод-
ное и вынужденное. Свободное движение жидкости является результатом различия плотностей еѐ по объѐму. Вынужденное движение жидкости побуждается работой вентиляторов, насосов.
Интенсивность свободного движения жидкости зависит от
коэффициента объемного расширения , некоторого характерного размера твѐрдого тела, омываемого жидкостью l, кинематической вязкости ν, ускорения силы тяжести g и разности температур между
поверхностью твѐрдого тела и жидкостью t tс tж . В целом интенсивность свободного движения жидкости характеризуется численным значением безразмерного комплекса, состоящего из указанных величин.
76
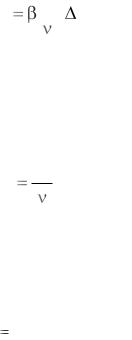
Gr |
gl3 |
t |
|
2 |
|||
|
(2.29) |
||
|
|
Комплекс (2.29) называется критерием Грасгофа. Интенсивность вынужденного движения жидкости зависит
от скорости движения жидкости w, характерного размера твѐрдого тела, омываемого жидкостью -l, кинематической вязкости жидкости
– ν. В целом интенсивность вынужденного движения жидкости определяется численным значением безразмерного комплекса, состоящего из этих величин.
Re wl
(2.30)
Комплекс (2.30) называется критерием Рейнольдса. 3 Температурные условия
Температурные условия при конвективном теплообмене характеризуются безразмерным отношением абсолютной температуры поверхности твердого тела к абсолютной температуре жидкости, поступающей на теплообмен.
|
|
|
Tc |
|
T |
|
|||
|
|
|
||
|
To |
(2.31) |
||
|
|
|
||
|
|
|
|
|
Здесь Тс - абсолютная температура поверхности твердого тела и To- абсолютная температура жидкости, поступающей на теплообмен. Отношение (2.30) называется температурным фактором.
4 . Форма и размеры теплообменной поверхности Форма и размеры теплообменной поверхности при конвек-
тивном теплообмене в безразмерном виде характеризуются геометрическими симплексами –Г1 ,Г2,…
Каждый такой симплекс представляет собой отношение какого - либо одного характерного линейного размера поверхности к другому.
Так, например поверхность цилиндрической трубы (рис.44) характеризуется одним симплексом.
77
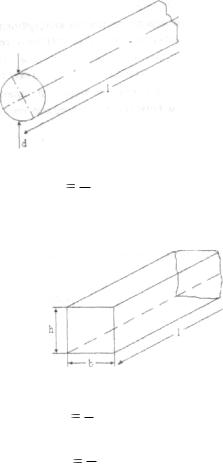
Рис. 44
Г |
l |
|
d |
|
|
|
(2.32) |
Поверхность прямоугольного канала (рис.45) характеризуется двумя симплексами
|
|
Рис 45 |
|
Г1 |
l |
|
|
b |
(2.33) |
||
|
l
Г 2 h (2.34)
Как видно, переход от одной формы теплообменной поверхности к другой влечет за собой изменение вида симплексов, а также их числа. Чем сложнее теплообменная поверхность, тем большим количеством геометрических симплексов она характеризуется.
2.2.3. Критериальные уравнения конвективного теплообмена
78
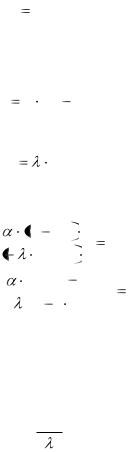
Из вышеприведенных рассуждений следует, что количество теплоты, передаваемой при конвективном теплообмене, зависит от критериев Прандтля, Грасгофа, Рейнольдса, температурного фактора и геометрических симплексов и, следовательно, должно существовать безразмерное соотношение следующему вида.
q |
|
|
|
|
|
|
f (Pr,Gr, Re,T , Г1 |
, Г2 |
...). |
||||
|
||||||
q0 |
||||||
|
|
|
|
(2.35) |
||
|
|
|
|
|
||
Здесь q – суммарный тепловой поток при конвективном теплообмене, обусловленный одновременным действием теплопроводности и конвекции жидкости, и описываемый
q |
a |
(tc |
tж ) |
|
|
|
|
|
(2.36) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и q0 часть этого потока, обусловленная действием только |
|||||||||||||||
теплопроводности жидкости |
|
|
|
|
|
|
|
|
|||||||
q0 |
|
|
|
grad |
t . |
|
|
|
|
|
(2.37) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставив (2.36) и (2.37) в (2.35) и умножив числитель и |
|||||||||||||||
знаменатель левой части (2.35) на некоторый размер |
l, получим |
||||||||||||||
|
|
|
tc |
|
tж |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (Pr,Gr, Re,T , Г1 , Г |
2 ,...) |
||||||||
|
|
|
|
|
gradt l |
||||||||||
|
|
|
|
|
|
|
|
|
|
(2.38) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
tc |
tж |
|
|
|
|
|
|
||
( |
|
)( |
) f (Pr,Gr, Re,T , Г1 , Г2 ,...) |
||||||||||||
|
|
l |
gradt |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
(2.39)
1я часть уравнения (2.39) представляет собой произведение двух безразмерных комплексов. Первый из этих комплексов характеризует явление конвективного теплообмена называется критерием Нуссельта.
Nu 
 l
l
(2.40)
где α - коэффициент теплоотдачи; l - некоторый характерный размер твѐрдого тела; λ - коэффициент теплопроводности жидкости.
Второй комплекс характеризует распределение температур в жидкости при конвективном теплообмене.
79
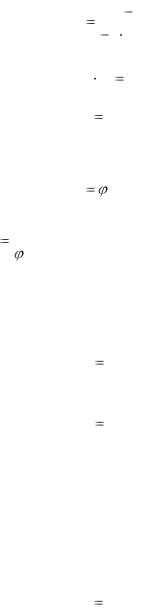
|
|
|
|
|
|
tc |
tж |
|
|
|
|
|||||||
|
|
Q |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
gradt |
|
|
|
(2.41) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перепишем (2.39) в виде |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Nu Q |
f (Pr,Gr, Re,T , Г1 , Г 2 ,...) |
(2.42) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Nu |
|
|
|
|
f (Pr,Gr, Re,T , Г1 , Г 2 ...) |
|
||||||||||
|
|
|
|
|
|
|
|
|
Q |
|
|
|
(2.43) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ показывает, что температурный комплекс Q являет- |
|||||||||||||||||
ся функцией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Q |
|
|
|
(Pr,Gr, Re,T , Г1 , Г 2 ,...) |
|
|||||||||||
|
С |
учетом |
(2.44) |
|
перепишем |
(2.43) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
f (Pr,Gr, Re,T , Г1 , Г 2 ...) |
|
|
|
|
|||||||||||||
Nu |
|
|
. |
|
|
|
|
|||||||||||
|
|
|
|
|
, Г1.Г 2 ,...) |
|
|
|
|
|||||||||
(Pr,Gr, Re,T |
|
|
|
|
||||||||||||||
Выражение (2.45) представляет собой критериальное уравнение конвективного теплообмена. Это уравнение справедливо для общего случая конвективного теплообмена. В частных случаях (2.45) упрощается. Так, при вынужденном движении жидкости критерий Грасгофа из числа аргументов выпадает
|
|
|
|
|
|
|
Nu |
(Pr,Re,T , Г1 , Г 2 |
,...) |
. |
(2.46) |
||
|
|
|
|
|
||
При чисто свободном движении жидкости из числа аргу- |
||||||
ментов выпадает критерий Рейнольдса |
|
|
||||
|
|
|
|
|
|
|
Nu |
(Pr,Gr,T , Г1 , Г 2 |
,...) |
|
(2.47) |
||
|
|
|
|
|
|
|
Для газов одинаковой атомности |
|
|
||||
Pr = const, |
|
|
(2.48) |
|||
а именно:
для одноатомных Pr ≈ 0.67; для двухатомных Pr ≈ 0.7; для трѐхатомных Pr ≈ 0.8;
и для четырѐх и выше Pr ≈1.
Для газов критериальное уравнение сокращается. Так, при вынужденном движении газа получим.
|
|
|
|
|
Nu (Re,T , Г1 , Г 2 |
,...) |
(2.49) |
||
|
|
|
|
|
Анализ показывает, что во многих случаях влияние темпе-
80
