Учебное пособие 800316

где 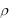- расстояние от площадки dF до начала координат, а J p - полярный момент инерции.

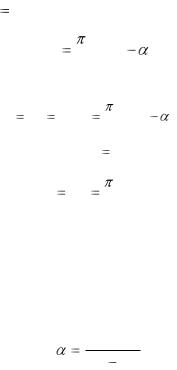
Рис. 4.3

Полученная формула позволяет легко определить осевой момент инерции круглого сечения относительно оси, проходящей через центр этого сечения.

Если D и d - соответственно наружный и внутренний диаметр сечения, а 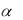d / D , то

Вследствие круговой симметрии

В случае сплошного круга 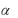0 , поэтому

4.3.4. Главные оси и главные моменты инерции Можно показать, что существуют по крайней мере две

взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю. Эти оси называются главными осями инерции сечения. Их положение определяется по формуле

Здесь 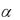- угол между главной осью инерции сечения и осью x.

Моменты инерции относительно главных осей экстремальны, т.е. осевой момент инерции относительно одной из главных осей наибольший, а относительно второй главной осинаименьший из всех моментов относительно осей с общим началом координат.

Моменты инерции относительно главных осей называются главными моментами инерции. Их величину можно опреде-

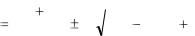
лить, если известны моменты инерции J x , J y , J xy относительно любых двух взаимно перпендикулярных осей:

5.ИЗГИБ

5.1.Расчѐты на прочность при изгибе

5.1.1.Внутренние силовые факторы Как уже указывалось, под изгибом понимают вид дефор-

мирования, при котором в поперечных сечениях стержня воз-

никают изгибающие моменты. Если наряду с этими момента-

ми возникают поперечные силы, изгиб называют поперечным,

в противном случае, т.е. если в поперечных сечениях действу-

ют только изгибающие моменты, изгиб называют чистым.

Стержень, работающий в основном на изгиб, принято в технической литературе называть балкой.

Ограничимся здесь рассмотрением случая прямого плос-

кого изгиба, когда все внешние силы, действующие на балку,

еѐ ось и одна из главных осей инерции поперечного сечения лежат в одной плоскости.

Условимся относительно правила знаков изгибающих мо-

ментов и поперечных сил. Как будет ясно из последующего изложения, это правило связано с направлением координатных осей. Пусть в дальнейшем ось y направлена вверх. Тогда неза-

висимо от направления оси z, совмещенной с осью балки,

можно принять следующее правило знаков.

Будем считать поперечную силу Q, возникающую в рас-

сматриваемом сечении в результате действия некоторой внеш-

ней силы, приложенной слева от сечения, положительной, если эта сила направлена вверх. Если же внешняя сила приложена справа от сечения, то вызываемая, ею поперечная сила счита-

ется положительной, когда внешняя сила направлена вниз. В

противных случаях поперечная сила считается отрицательной.

Таким образом, положительная поперечная сила вызывается внешней силой, момент которой относительно центра тяжести рассматриваемого сечения направлен по ходу часовой стрелки

(рис.5.1).

Если внешняя сила (или пара сил) приложена слева от рас-

сматриваемого сечения, то вызываемый ею изгибающий мо-

мент считается положительным, если момент этой силы (пары сил) направлен против хода часовой стрелки. Если же внешняя сила (или пара сил) приложена справа от сечения, то вызывае-

Поперечную силу и изгибающий момент определяют, ис-

пользуя метод сечений. Если мысленно рассечь балку в инте-

ресующем нас сечении, отбросить одну из полученных частей балки, заменив еѐ действие на оставшуюся часть поперечной силой и изгибающим моментом, и рассмотреть равновесие ос-

тавшейся части балки, легко увидеть, что поперечная сила в этом сечении, равна сумме взятых с учѐтом принятого правила знаков проекций всех приложенных к балке по одну сторону от сечения внешних сил на ось y. Изгибающий момент в этом сечении равен сумме взятых с учѐтом принятого правила зна-

ков моментов всех внешних сил, приложенных к балке по одну сторону от рассматриваемого сечения, относительно центра тяжести этого сечения.

В число указанных внешних сил входят как активные си-

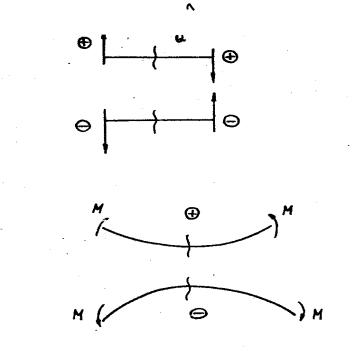
лы, обычно заданные, так и подлежащие обычно определению реакции опор. На рис. 5.2 схематично показаны основные ти-

пы опор балок.

Рис. 5.2

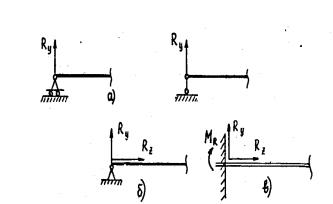
Опоры а – шарнирно подвижные. Они запрещают переме-

щение опирающегося на них сечения балки в направлении,

перпендикулярном некоторой плоскости (обычно в направле-

нии оси y). В соответствии с этим реакция шарнирно подвиж-

ной опоры направлена по перпендикуляру к указанной плоско-

сти. Опора б – шарнирно неподвижная. Она запрещает линей-

ные перемещения опирающегося на неѐ сечения балки. В со-

ответствии с этим реакция этой опоры представляет собой произвольно ориентированную в плоскости zoy силу, которую можно разложить на две составляющие вдоль координатных осей Rz и Ry. Заметим, что в рассматриваемых нами задачах всегда Rz = 0. Тем не менее, запрет перемещения вдоль оси Z

необходим для противодействия различным (пусть малым)

продольным нагрузкам на балку (скажем, ветровой нагрузки).

Если бы, например, двухопорная балка была установлена на двух шарнирно подвижных опорах, она легко превращалась бы в механизм. Опора в – защемление. Такая опора запрещает и линейные перемещения, и поворот опирающегося на неѐ се-

чения.

Реакциями такой опоры является произвольно направлен-

ная в плоскости ZOY силу, которую можно разложить на силы

Rz, Ry и опорный момент.

5.1.2. Теоремы Журавского.

Между нагрузкой на балку в окрестности рассматриваемо-

го сечения, поперечной силой и изгибающим моментом в этом сечении существует определѐнная связь, которую мы устано-

вим, рассмотрев равновесие элемента балки, выделенного двумя поперечными сечениями, отстоящими друг от друга на расстоянии dz (рис.5.3). Нагрузкой на этот элемент служит распределѐнная нагрузка, которую в силу малости dz можно