Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4624 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Воронежский государственный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Учебное пособие 800165

.pdf
Скачиваний:
2
Добавлен:
01.05.2022
Размер:
736.38 Кб
Скачать
☆

 

 

Объем

 

пирамиды

ABCD

равен

1

 

части

объема

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

параллелепипеда,

построенного

на

векторах AB 3,6,3 ,

AC 1,3, 2 ,

 

AD 2,2,2 . Находим смешанное произведение

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

этих

векторов ( AB AC ,AD)=

1

 

3

 

2

18.

Имеем

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

2

 

 

V

ABCD

 

1

 

18

 

3 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

10.

Даны

уравнения

двух

 

плоскостей П1 :

 

 

Задание

 

3x y z 2 ,

П2 :

x y z 3 0

и координаты точки M (1,3,2) .

Найти угол между плоскостями, отрезки, отсекаемые плоскостью П1 на координатных осях, уравнение плоскости, параллельной плоскости П2 , и проходящей через точку M , канонические уравнения прямой, являющейся линией пересечения плоскостей П1 , П2 , уравнение плоскости, проходящей через точку M и линию пересечения плоскостей

П1 , П2 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение. Укажем векторы нормали к плоскостям:n1 3,1,1 ,

n1 1, 1,1 . Косинус угла между плоскостями может быть найден

с помощью скалярного произведения векторов нормалей

cos φ=(n1, n1)/| n1 |·|n1|=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 1 1 ( 1) 1 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

3

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

2

1

2

1

2

1

2

( 1)

2

1

2

 

 

11 3

 

 

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для нахождения отрезков,

отсекаемых плоскостью П1 на

координатных осях, необходимо перейти от уравнения плоскости общего вида 3x y z 2 0 к уравнению плоскости в отрезках:

29

3

x

y

 

z

1

или

 

x

 

y

 

z

1 . Отрезки, отсекаемые плоскость

 

 

 

 

2

 

 

2

2

2

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

П

по осям

Ox, Oy, Oz , равны соответственно

a

2

, b 2,

 

1

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

c 2 .

 

 

 

 

 

 

 

 

 

 

Уравнение плоскости, проходящей через точку

 

M (1,3,2)

параллельно

плоскости

П2

( x y z 3 0 ), записывается с

использованием вектора нормали n1 1, 1,1 плоскости П2

как

вектора

 

нормали

 

 

искомой

плоскости

A x xM

B y yM C z zM 0 :

 

 

 

 

 

 

1

x 1 1 y 3 1 z 2 0

или x y z 0 .

 

 

 

 

Найдем

канонические уравнения прямой - линии

пересечения

плоскостей

П1

и

П2 . Опишем

прямую

как

геометрическое место точек, одновременно принадлежащих каждой из плоскостей, т.е. в виде системы

3x y z 2 0,x y z 3 0.

Направляющий вектор q прямой находится как векторное произведение векторов нормалей

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

j

 

k

 

 

 

 

 

q=

 

 

 

 

 

 

 

 

 

n1 n1

3

1

 

1

2 i

 

2 j

4 k .

 

 

 

 

1

1

1

 

 

 

 

 

 

 

 

Для нахождения точки Q , принадлежащей прямой,

положим xQ 0 .

Тогда для определения yQ

и

zQ получаем

систему

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

yQ zQ 2 0,

 

 

 

 

 

 

 

y

 

z

 

3 0.

 

 

 

 

 

 

Q

Q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

30

 

 

 

 

 

 

Решение системы дает yQ 12 , zQ 52 . Канонические

уравнения прямой

 

x xQ

 

 

y yQ

 

 

z zQ

в данном случае

 

 

x

 

 

 

 

y

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

имеют вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

1

 

 

 

 

z

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

4

 

 

Уравнение

плоскости,

 

содержащей

точку

M (1,3,2) и

 

 

 

y

1

 

 

 

 

z

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

прямую

 

 

2

 

 

 

 

2

 

 

,

получается

 

с

помощью вектора

2

2

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

нормали

n1

к

искомой

 

 

плоскости,

который

может быть

вычислен как векторное произведение направляющего вектора

q 2, 2, 4 и вектора QM

1,

7

,

1

 

:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

j

 

k

 

 

 

 

 

 

n1=

q QM

 

 

 

 

 

 

 

 

 

 

 

2

2

4

15 i

3 j

9 k .

 

 

1

7

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Искомое уравнение плоскости имеет вид

 

 

 

 

15 x 1 3 y 3

9 z 2 0 или 15x 3y 9z 24 0 .

 

Задание 11. Даны две прямые l1 (

 

x 1

y 2 z 3

),

 

 

2

 

 

1

 

1

l2 (

 

x 2 y 1

z 1

) и плоскость

П (

x 2y 3z 1 0 ).

 

 

3

 

1

 

 

0

 

Найти

угол

между прямой l2 и плоскостью

П , уравнение

плоскости, проходящей через прямую l1 параллельно прямой l2 , координаты точки пересечения прямой l1 и плоскости П .

31

Решение. Угол между прямой

 

x 2

 

y 1

 

z 1

и

 

3

 

 

 

 

1

0

 

плоскостью x 2y 3z 1 0 находится

как дополнительный

для угла между направляющим вектором q2= 3,1,0 и вектором

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

нормали n= 1,2, 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos(

) sin

(N l2 )

 

 

 

 

1 ( 3) 2 1 3 0

 

 

 

 

 

1

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

2

2

2 2

( 1)

2

2

 

 

10 14

 

 

 

 

 

 

 

 

 

 

N

 

l2

3

1 1 1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнение

 

плоскости,

проходящей

 

 

через

 

 

 

прямую

 

x 1 y 2

z 3

, параллельно

прямой

 

 

x 2

y 1 z 1

, в

 

2

 

 

1

 

 

1

 

 

 

3

 

1

 

 

0

 

данном случае может быть записано, если известна точка, принадлежащая плоскости, а также известен вектор нормали к искомой плоскости. В качестве точки плоскости можно взять точку E(1, 2,3) прямой l1 . Вектор нормали n1 должен быть

перпендикулярен направляющим векторам прямой q1= 2,1,1 и прямой q2= 3,1,0 , поэтому находится как векторное произведение указанных направляющих векторов

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

j

k

 

 

 

n1= q1 q2

 

 

 

 

2

1

1

i

3 j

5 k .

 

 

3

1

0

 

 

 

 

 

 

 

 

 

 

 

Витоге уравнение плоскости имеет вид:

x 1 3 y 2 5 z 3 0 или x 3y 5z 20 0 .

Для нахождения точки пересечения этой прямой l1 с плоскостью П ( x 2y 3z 1 0 ) приведем канонические

уравнения прямой

x 1

y 2

z 3

к параметрическому виду:

2

 

 

1

 

1

 

 

 

 

 

 

 

 

32

 

x 2t 1y t 2

z t 3

и найдем общую точку прямой и плоскости АВС:

14(14k 2) 6(6k 2) 11(5 11k) 10 0 ; (196 36 121)k 10 28 12 55 ;

k 105353 0,3.

Получим искомые координаты точки F пересечения прямой с плоскостью АВС :

xF 14 0,3 2;

 

xF 2,2;

 

0,3 2;

 

 

0,2;

yF 6

yF

 

 

 

 

1,7.

z F 11 0,3 5;

z F

Задание

12.

Привести общее уравнение кривой

x2 4 y2 4x 8y 4 0

к каноническому виду и построить

полученную кривую.

Решение. Выделяя полные квадраты , преобразуем левую часть уравнения. Имеем

(x2 2 2x 4 4) 4( y 2 2y 1 1) 4 0 ;

 

 

 

(x 2)2 4( y 1)2 4 ;

 

 

 

(x 2)2

 

( y 1)

2

1 .

 

 

 

4

1

 

 

 

 

 

 

 

 

 

Вводя новые координаты X x 2,Y y 1, получаем

 

X 2

 

Y 2

1.

 

 

 

 

 

 

 

 

 

 

 

4

 

1

 

 

 

 

 

 

 

Таким образом получено уравнение эллипса с центром в

точке

О 2;1 :

x 2 3y 2

x 4y 2 0 .

 

 

 

1

 

 

 

 

 

33

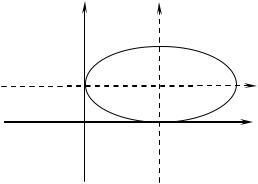
y Y

1

O1

X

O

2

x

34

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры/ Д.В. Беклемишев. М.: Наука, 1980.

2.Ефимов Н.В. Краткий курс аналитической геометрии/ Н.В. Ефимов. М.: Наука, 1975

3.Ефимов Н.В. Квадратичные формы и матрицыН.В. Ефимов. М.: Наука, 1972.

4.Бугров Я.С., Никольский С.М. Высшая математика. Элементы линейной алгебры и аналитической геометрии/ Я.С. Бугров, С.М. Никольский. М.: Наука, 1980.

5.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. пособие для студентов втузов/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова.

М.: Высш. шк., 1986. Ч.1.

6.Клетеник Д.В. Сборник задач по аналитической геометрии/ Д.В. Клетеник. М.: Наука, 1975.

35

СОДЕРЖАНИЕ

Задание № 1………………………………………….1 Задание № 2………………………………………….2 Задание № 3………………………………………….6 Задание № 4………………………………………….8 Задание № 5………………………………………….9 Задание № 6………………………………………….10 Задание № 7………………………………………….11 Задание № 8………………………………………….12 Задание № 9………………………………………….13 Задание № 10…………………………..….……………14 Задание № 11…………………………………………15 Задание № 12…………………………………………18 Примеры решения заданий ………………………...20 Библиографический список………..… … ……….35

36

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к типовому расчету по дисциплине «Математика» разделу “Линейная алгебра и аналитическая геометрия”

для студентов направления 15.03.01 «Машиностроение» профиль («Оборудование и технология сварочного производства») очной формы обучения

Составители: Горбунов Валерий Викторович

Костина Татьяна Ивановна Соколова Ольга Анатольевна

В авторской редакции

Компьютерный набор О.А. Соколовой

Подписано к изданию 20.11.2015.

Уч.- изд. л. 2,2. “C“.

ФГБОУ ВПО «Воронежский государственный технический университет»

394026 Воронеж, Московский просп., 14

37

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности