3. Определение запаса усталостной прочности

Запас усталостной прочности для случая одноосного напряженного состояния определяется по формуле:

Запас усталостной прочности для чистого сдвига (кручения) определяется по формуле:

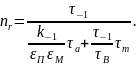
Для наиболее часто встречающихся на практике случаев расчета при двуосном напряженном состоянии 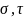общепринятой формулой эмпирической формулой является формула Гафа и Полларда:

где 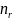– искомый запас усталостной прочности; 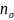- запас прочности в предположении, что касательные напряжения отсутствуют; - запас по касательным напряжениям, в предположении, что .

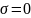4. Примеры расчетов вала с галтелью на прочность

Рассмотрим примеры расчета ступенчатого вала для различных случаев нагружения.

Пример 1 – кручение по несимметричному циклу. .

Пример 2 – изгиб по симметричному циклу. .

Пример 3 – изгиб (симметричный цикл, r ) и кручение по одностороннему циклу (напряжение меняется от 0 в одну сторону, ).

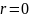Пример 1

Вал с галтелью работает на кручение по несимметричному циклу [3] .

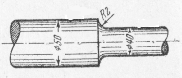
Наибольшее значение крутящего момента 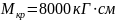, наименьшее значение . механические характеристики материала: , , . Определить запас прочности.

Решение

Номинальные характеристики цикла

откуда

Эффективный коэффициент определяем по справочным данным (рис. 10).

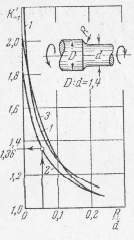
Рис. 10. Эффективный коэффициент концентрации

На рис. 11 представлена кривая , позволяющая получить значение для других соотношений .

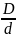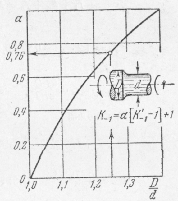
Рис. 11. Зависимость коэффициента чувствительности

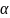от отношения диаметров вала

Определяем для вала с отношением диаметров На графике (рис.10) по кривой 2 ( ) для соотношения 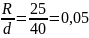получим По графику (рис.11) определим при . Тогда 0,76(1,36-1)+1=1,27. Вал шлифованный, поэтому 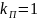(для изгиба и кручения).

С кривой 2 (рис.9) для диаметра снимаем значение .

Подсчитываем значение запаса усталостной прочности для кручения:

Пример 2

Вращающийся круглый ступенчатый вал изгибается постоянным моментом М_изг. Вал изготовлен из углеродистой стали с пределом прочности и пределом выносливости при изгибе (симметричный цикл). Диаметры вала и галтель имеет радиус [4].

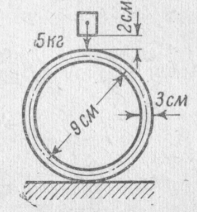
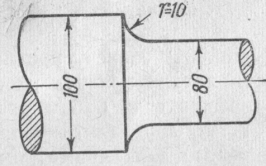
Определить наибольшую допускаемую величину момента М. Коэффициент запаса прочности по отношению к пределу выносливости детали принять равным n

Решение

Величина предела выносливости детали может быть определена по формуле:

где - передел выносливости, определенный лабораторным путем на малых образцах, – действительный коэффициент концентрации напряжений для малого образца и - масштабный коэффициент. При этом величина определяется по формуле:

(см. предыдущий пример).

Величину можно определить по графикам в справочной литературе и по приблизительной таблице из [5].

Коэффициенты концентрации

K’-₁

При имеем

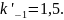
По графику (рис. 12, [5]) путем линейной интерполяции для стали с , находим величину коэффициента чувствительности .

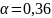Таким образом

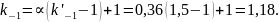
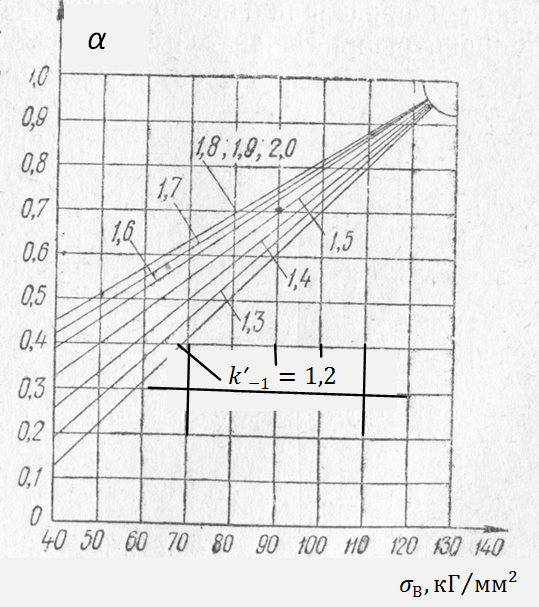
Рис. 12. Зависимость коэффициента чувствительности

от предела прочности материала

для различных значений

Величину коэффициента для детали из углеродистой стали при умеренной концентрации напряжений определяем по кривой 2 рис. 13 (графики можно применять для гладких образцов только при изгибе и кручении, а для образцов с концентраторами напряжений – при всех видах напряженного состояния); при 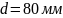имеем

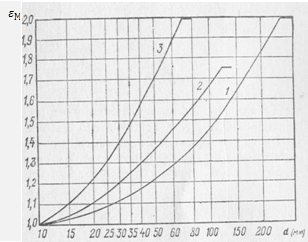
Рис. 13. Зависимость масштабного коэффициента от абсолютных размеров (диаметра d) для деталей:

1. из углеродистой стали при отсутствии концентрации напряжений;

2. из углеродистой стали при умеренной концентрации напряжений 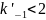и для деталей из легированной стали при отсутствии концентратора напряжений;

3. из легированной стали при наличии концентратора напряжений

Предел выносливости детали (вала) при симметричном цикле изменения напряжений равен:

Допускаемое напряжение равно:

Наибольшую допускаемую величину изгибающего момента М_изг определяем из условия прочности:

Откуда

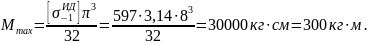
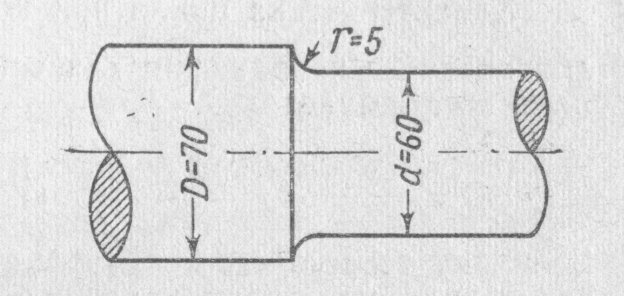
Пример 3

Круглый вал диаметром 60 мм, имеющий в месте перехода к диаметру 70 мм галтель радиусом 5 мм, изготовлен из углеродистой стали, для которой

Вал изгибается моментом, меняющимся от 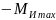до , и скручивается моментом, меняющимся от 0 до 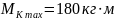; при этом наибольших и наименьших своих значений изгибающий и крутящий моменты достигают одновременно. Коэффициент динамической нагрузки 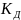для переменной составляющей цикла нормальных и касательных напряжений равен 2; коэффициент запаса прочности n =1,8.

Проверить прочность вала.

Решение

Условие прочности вала, подвергающегося одновременно изгибу и кручению, может быть написано так:

.

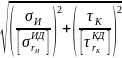
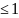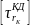Здесь и - допускаемые напряжения при изгибе и кручении, определяемые для детали в зависимости от степени асимметрии цикла нормальных и касательных напряжений.

Определим и .

Характеристика цикла при изгибе:

Величину допускаемого напряжения при изгибе (симметричный цикл) определим по формуле:

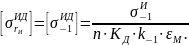
Величину теоретического коэффициента концентрации напряжений при изгибе вала с галтелью находим по таблице 1. Для отношения 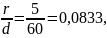применяя линейную интерполяцию между значениями при

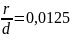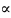и при , имеем Величину коэффициента чувствительности определяем по графику рис.12; при 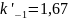и имеем 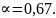Таким образом

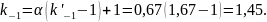
Величину масштабного коэффициента определяем по кривой 2 графика на рис. 13, при 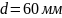имеем 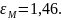Так как при 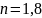и , то

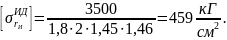
Характеристика цикла на кручение:

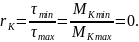
Величину допускаемого напряжения для симметричного цикла при кручении определяем по формуле:

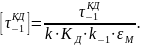
Величину теоретического коэффициента концентрации напряжений при кручении вала с галтелью находим по табл. 1.

Для отношения значение 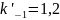при значение . Интерполируя эти значения получим для соотношения значение . Величину коэффициента чувствительности определяем по графику рис.12; при и имеем

Поэтому

Величина масштабного коэффициента та же, что и при изгибе; Таким образом, допускаемое напряжение для симметричного цикла при кручении равно

.

Допускаемое напряжение для постоянного цикла при кручении равно:

Величину допускаемого напряжения при кручении детали для цикла с характеристикой определяем по формуле:

.

Наибольшие действительные значения напряжений 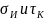при изгибе и кручении вала равны:

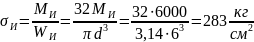
и

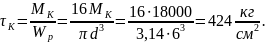
Подставив в условие прочности значения , а также найденные ранее значения и , имеем

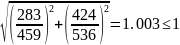
Прочность вала обеспечена.