3.2. Несимметричные сечения

3.13. Для сечения, состоящего из равнобокого уголка 100х100х10 и полосы 200х40 мм (рис. 3.13), определить положение главных центральных осей инерции и значения моментов инерции относительно этих осей.

Решение

Положение главных центральных осей по отношению к произвольным центральным осям x_C, y_C определяется углом α₀

, где соответ-ственно центробежный и осевые моменты инерции относительно произвольных центральных осей x_C, y_C.

М оменты инерции относительно главных центральных осей

.

Определение значений главных центральных моментов инерции производим в соответствии с алгоритмом, приведенным в [1].

1. Вычерчиваем сечение в масштабе. Проводим вспомогательные оси координат .

2. Разбиваем составное сечение на две простые фигуры - полосу (1) и равнобокий уголок (2) (см. рис. 3.13). Для каждой простой фигуры определяем площадь, координаты центра тяжести относительно вспомогательных осей и заносим в табл. 3.1. При этом центр тяжести прямоугольника и его площадь подсчитываем, а площадь равнобокого уголка и координаты его центра тяжести определяем с помощью таблиц сортамента прокатной стали (см. Приложение 1). Проводим центральные оси для каждого элемента, параллельные вспомогательным осям . Для прямоугольника оси являются главными центральными осями (как оси симметрии).

3. Определяем координаты центра тяжести всего сечения в системе вспомогательных осей и

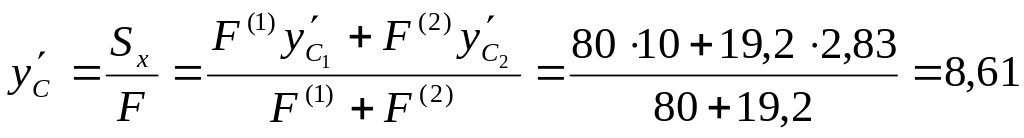см,

см.

Через центр тяжести составного сечения С проводим центральные оси сечения , параллельные вспомогательным осям. Заметим, что центр тяжести составного сечения С должен лежать на прямой С₁С₂, соединяющей центры тяжести прямоугольника и уголка, что можно использовать для проверки правильности определения положения центра тяжести. Определяем координаты центров тяжести уголка и прямоугольника в системе центральных осей и заносим их в

табл. 3.1.

4. Пользуясь Приложениями 1, 2, рассчитываем или берем из сортамента прокатной стали осевые и центробежные моменты инерции прямоугольника и равнобокого уголка относительно собственных центральных осей и заносим их значения в табл. 3.1. Для прямоугольника

см⁴, = 0,

см⁴.

Для равнобокого уголка (рис. 3.14)

см⁴, см⁴, см⁴.

Для определения центробежного момента инерции уголка относительно осей воспользуемся формулой преобразования момента инерции при повороте осей координат [1], учитывая, что оси - главные (ось х₂ является осью симметрии уголка) и, следовательно, , а угол α = -45⁰, так как он отсчитывается от оси к по ходу часовой стрелки

= см⁴.

5. Пользуясь формулами преобразования моментов инерции при параллельном переносе осей координат [1], определяем осевые и центробежные моменты инерции прямоугольника и равнобокого уголка относительно центральных осей всего сечения. Вычисления удобно свести в табл. 3.1.

6. Суммируя соответственно осевые и центробежные моменты инерции прямоугольника и равнобокого уголка относительно центральных осей всего сечения, рассчитываем осевые и центробежный моменты инерции составного сечения относительно его центральных осей

,

М оменты инерции элемента, см4	Относительно центральных осей сечения		-104,53 -536,65 -641,28
			177,36 469,54 646,90
			2821,24 820,44 3641,68
	Относительно собственных центральных осей		0 -104,95
			106,67 179,00
			2666,6 179,00
Координаты центра тяжести элемента, см	Относительно центральных осей сечения		-1,39 5,78
			0,94 -3,89
	Относи-тельно вспомо-гатель-ных осей		10,00 2,83 8,61
			2,00 6,83 2,94
Пло-щадь эле-мента Fi, см			80,00 19,20 99,20
Номер элеме-нта			1 2 Для всего сечения

Так как угол , то откладываем его от оси против хода часовой стрелки. Проводим главные центральные оси инерции x и y, где ось х повернута относительно оси на угол против хода часовой стрелки, а ось y перпендикулярна оси х.

8. Рассчитываем значения главных центральных моментов инерции сечения:

см⁴.

Так как > то ось с максимальным моментом инерции должна составлять с осью х_с меньший угол. Следовательно, в данном случае

см⁴, см⁴.

9. Проверка. Для главных центральных осей x, y должны удовлетворяться условия

.

В данном случае

см⁴.

см⁴.

Относительная ошибка составляет:

,

что допустимо. Следовательно величины главных центральных моментов инерции и , а также положение главных центральных осей x и y найдены верно.

3.14. Для сечений, приведенных на рис. 3.15, определить положение главных центральных осей инерции и значения главных центральных моментов инерции.

3.15. Для заданного сечения (рис. 3.16) определить размер “c”, если статический момент этого сечения .

3.16. Для составного сечения (рис. 3.17) рассчитать центробежный момент инерции относительно двух взаимно перпендикулярных центральных осей этого сечения.