
- •1. Растяжение (сжатие)
- •1.1. Статически определимые системы
- •1.2. Статически неопределимые системы
- •1.3. Экспериментальное исследование растяжения (сжатия)
- •2. Кручение валов круглого сечения
- •2.1. Статически определимые системы
- •2.2. Статически неопределимые системы
- •2.3. Экспериментальное исследование кручения
- •3. Геометрические характеристики
- •3.2. Несимметричные сечения
- •4. Изгиб
- •4.2.2. Статически – неопределимые рамы и кривые брусья малой кривизны.
- •394026 Воронеж, Московский просп., 14
2.3. Экспериментальное исследование кручения
2.29. По результатам испытаний стального
круглого образца на кручение получена
табличная зависимость «крутящий момент
– угол закручивания
»
(табл. 2.1). Выполнить экспериментальную
проверку закона Гука при кручении,
вычислить экспериментальное значение
модуля сдвига
![]() и сравнить его с теоретическим значением
,
если расчетная длина образца
и сравнить его с теоретическим значением
,
если расчетная длина образца
![]() ,
диаметр рабочей части образца
,
диаметр рабочей части образца
![]() ,
коэффициент Пуассона
,
коэффициент Пуассона
![]() ,
модуль упругости
.
,
модуль упругости
.
Таблица 2.1
Крутящий момент
,
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
Угол закручивания
|
0 |
0,88 |
1,80 |
2,75 |
3,75 |
4,75 |
5,75 |
6,75 |
7,75 |
2.30. При испытании на кручении стального
образца длиной 20 см и диаметром 20 мм
установлено, что при крутящем моменте
![]() угол закручивания равен 0,026 рад. Предел
упругости достигнут при крутящем моменте
270
.
Определить величину модуля сдвига и
предел упругости при кручении.
угол закручивания равен 0,026 рад. Предел
упругости достигнут при крутящем моменте
270
.
Определить величину модуля сдвига и
предел упругости при кручении.
2.31. Возрастание крутящего момента
![]() при испытаниях на кручение стального
цилиндрического образца оказалось
равным 5
,
при этом приращение угла закручивания
при испытаниях на кручение стального
цилиндрического образца оказалось
равным 5
,
при этом приращение угла закручивания
![]() на длине 20 см. Вычислить модуль сдвига
материала образца и коэффициент Пуассона,
если модуль упругости
,
диаметр образца 16 мм.
на длине 20 см. Вычислить модуль сдвига
материала образца и коэффициент Пуассона,
если модуль упругости
,
диаметр образца 16 мм.
2.32. Полый вал закручивается моментами
,
приложенными к его концам. Посередине
вала под углом
![]() к его оси установлен тензометр с базой
к его оси установлен тензометр с базой
![]() и увеличением
и увеличением
![]() .
Приращение показаний тензометра
.
Приращение показаний тензометра
![]() соответствует увеличению крутящего
момента
соответствует увеличению крутящего
момента
![]() .
Вычислить модуль сдвига материала и
приращение угла закручивания вала, если
его длина
,
а диаметры сечения
.
Вычислить модуль сдвига материала и
приращение угла закручивания вала, если
его длина
,
а диаметры сечения
![]() ,
,
![]() .
.
3. Геометрические характеристики
плоских сечений
3.1. Симметричные сечения
3.1.1. Сечения с двумя и более осями симметрии
3 .1.
Поперечное сечение сварной балки состоит
из двутавра №18 и двух швеллеров №22
(рис. 3.1). Вычислить осевые моменты
сопротивления.
.1.
Поперечное сечение сварной балки состоит
из двутавра №18 и двух швеллеров №22
(рис. 3.1). Вычислить осевые моменты
сопротивления.
Решение
Моменты сопротивления сечения Wx = Jx/ymax, Wy = Jy/xmax, где Jx, Jy - главные центральные моменты инерции; ymax , xmax-координаты точек сечения, наи-более удаленных от главных центральных осей.
Для заданного сечения оси x, y - главные центральные оси, т.к. они являются осями симметрии.
Разбиваем сечение на три элемента – двутавр(1) и два швеллера(2,3).
Все необходимые для расчета моментов сопротивления вели-чины устанавливаем из таблицы сортамента прокатной стали
(см. Приложение 1): Jx(1) = 1290 см4, Jy(1) = 82,6 см4, h(1) = 18 см,
JxC2(2) = JxC3(3) = 151 см4, Jy(2) = Jy(3) = 2110 см4, h(2) = h(3) = 22 см, b(2) = b(3) = 8,2 см, F(2) = F(3) = 26,7 см2, y0(2) = y0(3) = 2,21 см.
Момент инерции сечения относительно оси y
Jy
= Jy(1)
+ Jy(2)
+ Jy(3)
= 82,6 +
![]() =
4302,6 см4.
=
4302,6 см4.
Момент сопротивления сечения относительно оси y
Wy =
![]() =
=
![]() =
=
![]() = 391,1 см3.
= 391,1 см3.
Используя формулы изменения момента инерции при параллельном переносе осей координат, определяем момент
инерции сечения относительно оси x:

![]()
= 1290 + 2(151 + (18/2 + 2,21)2
![]() =
8302,5 см4.
=
8302,5 см4.
Момент сопротивления сечения относительно оси х
![]() см3.
см3.
3.2. Определить осевые моменты сопротивления для сечений, показанных на рис. 3.2.
3.3. Определить осевые и полярный моменты сопротивления сечения (рис. 3.3).
3.4. Установить, как изменятся момент инерции и момент сопротивления квадрата относительно оси х, если сечение повернуть на угол 450 относительно этой оси (рис. 3.4).
3.5. Из круглого бревна диаметром d необходимо выпи-лить брус прямоугольного сечения, осевой момент сопротивле-ния которого относительно оси симметрии y имел бы наиболь-шее значение (рис. 3.5). Определить из этого условия размеры b и h.
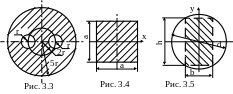 3.6.
Для поперечного сечения колонны,
состоящего из двух швеллеров №24 и двух
пластин размером 300х12 мм (рис.3.6),
определить размер “с” из условия, чтобы
все цен-тральные оси сечения были
главными. Вычислить соответствующий
момент инерции.
3.6.
Для поперечного сечения колонны,
состоящего из двух швеллеров №24 и двух
пластин размером 300х12 мм (рис.3.6),
определить размер “с” из условия, чтобы
все цен-тральные оси сечения были
главными. Вычислить соответствующий
момент инерции.
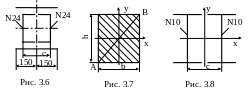
3.7. Определить момент инерции прямоугольника относительно оси, совпадающей с диагональю АВ (рис. 3.7).
3.8. На каком расстоянии “c” нужно расположить два двутавра №10 (рис. 3.8), чтобы момент инерции Jy этого составного сечения равнялся 780 см4.
3.1.2. Сечения с одной осью симметрии
3.9. Для круглого сечения с прямоугольной полостью (рис.3.9) вычислить осевые моменты сопротивления, приняв d = 12 мм.
Решение
Моменты сопротивления сечения Wx = Jx / ymax, Wy = Jy / xmax, где Jx, Jy – главные центральные моменты инерции; ymax, xmax – координаты точек сечения, наиболее удаленных от главных центральных осей.
Т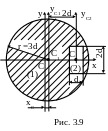 ак
как ось Х является осью симметрии, то
для заданного сечения она является
главной центральной осью.
ак
как ось Х является осью симметрии, то
для заданного сечения она является
главной центральной осью.
Тогда для установления положения центра тяжести сечения достаточно определить одну координату ХС. При ее оп-ределении заштрихованную площадь можно рассматривать как разность площадей круга (1) и прямоугольника (2), (см. рис. 3.9).
Тогда
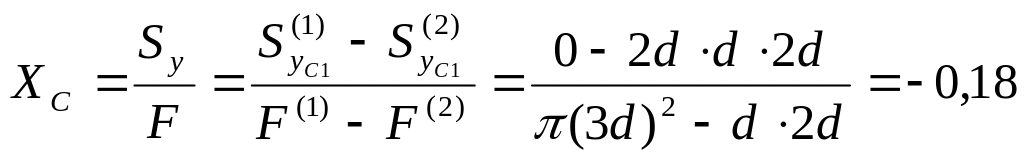 см.
см.
Пользуясь Приложением 2, определяем моменты инерции простых фигур, входящих в сечение, относительно собственных центральных осей
![]() =
131,85 см4.
=
131,85 см4.
![]() =
1,38 см4.
=
1,38 см4.
![]() =
0,35 см4.
=
0,35 см4.
Рассматриваем моменты инерции заштрихованного сечения относительно оси Х как разность моментов инерции круга и прямоугольника
![]() 130,47
см4.
130,47
см4.
Момент сопротивления сечения относительно оси Х
![]() =
36,24 см3.
=
36,24 см3.
Используя формулу изменения момента инерции при параллельном переносе осей координат, определяем момент инерции сечения относительно оси y
![]()
=![]() =126,91
см4.
=126,91
см4.
Момент сопротивления сечения относительно оси y
![]() см3.
см3.
3.10. Для сечений, показанных на рис. 3.10, определить осевые моменты сопротивления.

3.11. Для составных сечений, приведенных на рис. 3.11, вычислить осевые моменты сопротивления.
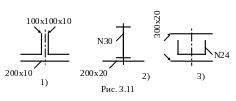
3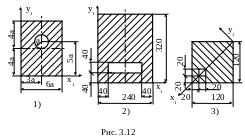 .12.
Для приведенных на рис. 3.12 сечений
определить центробежный момент инерции
относительно осей x1,
y1.
.12.
Для приведенных на рис. 3.12 сечений
определить центробежный момент инерции
относительно осей x1,
y1.
