
- •ЭЛектромагнитная индукция и магнитное поле в веществе
- •ЭЛектромагнитная индукция и магнитное поле в веществе
- •394026 Воронеж, Московский просп., 14
- •ЭЛектромагнитная индукция и магнитное поле в веществе
- •Электромагнитная индукция Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.Магнитное поле в веществе. Энергия магнитного поля Основные законы и формулы
- •П римеры решения задач
- •Задачи для самостоятельного решения
- •Библиографический список
- •Содержание
- •3. Магнитное поле в веществе.Энергия магнитного
Задачи для самостоятельного решения
Электродвижущая сила индукции
1. Прямой провод длиной l=10см помещен в однородное магнитное поле с индукцией В=1Тл. Концы его замкнуты гибким проводом, находящимся вне поля. Сопротивление R всей цепи равно 0,4 Ом. Какая мощность Р потребуется для того, чтобы двигать провод перпендикулярно линиям индукции со скоростью v=20м/с ?
Ответ: Р=10Вт
2. К источнику тока с ЭДС
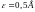 и ничтожно малым внутренним сопротивлением
присоединены два металлических стержня,
расположенных горизонтально и параллельно
друг другу. Расстояние l
между стержнями равно 20см. Стержни
находятся в однородном магнитном поле,
направленном вертикально. Магнитная
индукция В=1,5Тл. По стержням под
действием сил поля скользит со скоростью
v=1м/с прямолинейный
провод сопротивлением R=0,02Ом.
Сопротивление стержней пренебрежимо
мало. Определить:
и ничтожно малым внутренним сопротивлением
присоединены два металлических стержня,
расположенных горизонтально и параллельно
друг другу. Расстояние l
между стержнями равно 20см. Стержни
находятся в однородном магнитном поле,
направленном вертикально. Магнитная
индукция В=1,5Тл. По стержням под
действием сил поля скользит со скоростью
v=1м/с прямолинейный
провод сопротивлением R=0,02Ом.
Сопротивление стержней пренебрежимо
мало. Определить:
1) ЭДС индукции
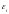 ;
2) силу F, действующую
на провод со стороны поля; 3) силу тока
I в цепи; 4) мощность
;
2) силу F, действующую
на провод со стороны поля; 3) силу тока
I в цепи; 4) мощность
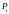 ,
расходуемую на движение провода; 5)
мощность
,
расходуемую на движение провода; 5)
мощность
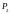 ,
расходуемую на нагревание провода; 6)
мощность
,
расходуемую на нагревание провода; 6)
мощность
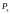 ,
отдаваемую в цепь источника тока.
,
отдаваемую в цепь источника тока.
Ответ:
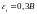 ;
;
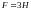 ;
;
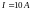 ;
;
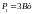 ;
;
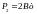 ;
;
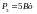
3. В однородном магнитном поле с
индукцией В=0,4Тл в плоскости,
перпендикулярной линиям индукции поля,
вращается стержень длиной l=10см.
Ось вращения проходит через один из
концов стержня. Определить разность
потенциалов U на концах
стержня при частоте вращения
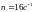 .
.
Ответ:
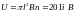
4. Рамка площадью
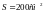 равномерно вращается с частотой
равномерно вращается с частотой
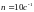 относительно оси, лежащей в плоскости
рамки и перпендикулярно линиям индукции
однородного магнитного поля (В=0,2
Тл). Каково среднее значение ЭДС
индукции
относительно оси, лежащей в плоскости
рамки и перпендикулярно линиям индукции
однородного магнитного поля (В=0,2
Тл). Каково среднее значение ЭДС
индукции
![]() за время, в течение которого магнитный
поток, пронизывающий рамку, изменится
от нуля до максимального значения?
за время, в течение которого магнитный
поток, пронизывающий рамку, изменится
от нуля до максимального значения?
Ответ:
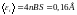
5. В однородном магнитном поле с
индукцией В=0,35Тл равномерно с
частотой
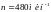 вращается рамка, содержащая N=500
витков площадью
вращается рамка, содержащая N=500
витков площадью
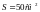 .
Ось вращения лежит в плоскости рамки и
перпендикулярна линиям индукции.
Определить максимальную ЭДС индукции
.
Ось вращения лежит в плоскости рамки и
перпендикулярна линиям индукции.
Определить максимальную ЭДС индукции
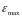 ,
возникающую в рамке.
,
возникающую в рамке.
Ответ:
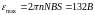
6. Магнитная индукция В поля
между полюсами двухполюсного генератора
равна 0,8 Тл. Ротор имеет N=100
витков площадью
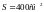 .
Определить частоту n
вращения якоря, если максимальное
значение ЭДС индукции
.
Определить частоту n
вращения якоря, если максимальное
значение ЭДС индукции
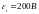 .
.
Ответ:
 n
= 600мин-1
n
= 600мин-1
7. Короткая катушка, содержащая
N=1000 витков, равномерно
вращается в однородном магнитном поле
с индукцией В=0,04Тл с угловой
скоростью
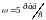 относительно оси, совпадающей с диаметром
катушки и перпендикулярной линиям
индукции поля. Определить мгновенное
значение ЭДС индукции
для тех моментов времени, когда плоскость
катушки составляет угол
относительно оси, совпадающей с диаметром
катушки и перпендикулярной линиям
индукции поля. Определить мгновенное
значение ЭДС индукции
для тех моментов времени, когда плоскость
катушки составляет угол
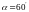 с линиями индукции поля. Площадь S
катушки равна 100
с линиями индукции поля. Площадь S
катушки равна 100
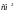 .
.
Ответ: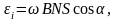
Количество электричества, протекающее в контуре при изменении магнитного потока
8. Между полюсами электромагнита
помещена катушка, соединенная с
баллистическим гальванометром. Ось
катушки параллельна линиям индукции.
Катушка сопротивления
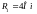 имеет N=15 витков
площадью
имеет N=15 витков
площадью
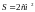 .
Сопротивление
.
Сопротивление
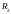 гальванометра равно 46 Ом. Когда ток
в обмотке электромагнита выключили, по
цепи гальванометра протекло количество
электричества Q=90
мкКл. Вычислить магнитную индукцию
В поля электромагнита.
гальванометра равно 46 Ом. Когда ток
в обмотке электромагнита выключили, по
цепи гальванометра протекло количество
электричества Q=90
мкКл. Вычислить магнитную индукцию
В поля электромагнита.
Ответ: В=1,5Тл
9. Рамка из провода сопротивление R=0,01Ом равномерно вращается в однородном магнитном поле с индукцией В=0,05Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь S рамки равна
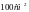 .
Найти, какое количество электричества
Q протечет через рамку за
время поворота ее на угол
.
Найти, какое количество электричества
Q протечет через рамку за
время поворота ее на угол
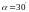 в следующих трех случаях: 1) от
в следующих трех случаях: 1) от
![]() до
до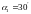 ;
2) от
;
2) от
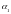 до
до
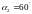 ;
3) от
;
3) от
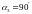
Ответ:
1)
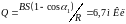
2)
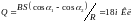
3)
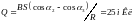
10. Тонкий медный провод массой m=1г согнут в виде квадрата, и концы его замкнуты. Квадрат помещен в однородное магнитное поле (B=0,1 Тл) так, что плоскость его перпендикулярна линиям индукции поля. Определить количество электричества Q, которое протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
Ответ:
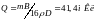 (D – плотность меди.)
(D – плотность меди.)
11. На расстоянии =1м от длинного прямого провода с током I=1кА находится кольцо радиусом r=1см. Кольцо расположено так, что поток, пронизывающий его, максимален. Определить количество электричества Q, которое протечет по кольцу, когда ток в проводнике будет выключен. Сопротивление R кольца 10Ом.
Указание. Поле в пределах кольца считать однородным.
Ответ:
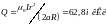
12. По длинному прямому проводу течет
ток. Вблизи провода расположена квадратная
рамка из тонкого провода сопротивлением
R=0,02Ом. Провод
лежит в плоскости рамки и параллелен
двум ее сторонам, расстояние до которых
от провода соответственно равны
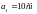 ,
,
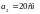 .
Найти силу тока I в
проводе, если при его включении через
рамку протекло количество электричества
Q=693 мкКл.
.
Найти силу тока I в
проводе, если при его включении через
рамку протекло количество электричества
Q=693 мкКл.
Ответ:
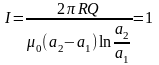 кА
кА
2. САМОИНДУКЦИЯ И ВЗАИМОИНДУКЦИЯ.
ИНДУКТИВНОСТЬ
Основные законы и формулы
Электродвижущая сила самоиндукции
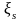 ,
возникающая в замкнутом контуре при
изменении силы тока в нём
,
возникающая в замкнутом контуре при
изменении силы тока в нём
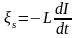 ,
или
,
или
![]() ,
,
где L – индуктивность контура.
Потокосцепление контура
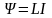 ,
,
где L – индуктивность контура.
Индуктивность соленоида (тороида)
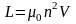
Примеры решения задач
1. Используя условие задачи 6 главы 4 [4] рассчитать индуктивность данного тороида.
Решение
Магнитный
поток через поперечное сечение тороида
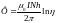 (см. решение задачи 6 главы 4 [4]).
(см. решение задачи 6 главы 4 [4]).
Индуктивность его найдем следующим образом
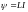 ,
L=ψ/I=NΦ/I,
,
L=ψ/I=NΦ/I,
где
L – индуктивность,
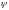 - потокосцепление.
- потокосцепление.
Таким
образом,
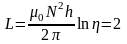 мГн.
мГн.
2. Найти индуктивность L длинного соленоида. Число витков на единицу длины равно n, а длина соленоида l.
Решение
Магнитное
поле внутри соленоида

где I – ток в обмотке соленоида.
Магнитный
поток через все витки
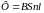 ,
,
где
S – площадь поперечного
сечения соленоида. С другой стороны
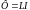 .
.
Таким
образом,
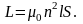
3. Найти индуктивность соленоида длины l, обмоткой которого является медная проволока массы m. Сопротивление обмотки R. Диаметр соленоида значительно меньше его длины.
Решение
Используем,
найденное в задаче 2, выражение
индуктивности соленоида
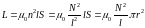 ,
,
где S – площадь поперечного сечения катушки, N – количество витков, r – радиус витка катушки.
Найдем
длину медной проволоки
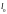 навитой на катушку радиуса r
навитой на катушку радиуса r
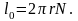
Таким
образом,
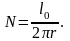
Найдем соотношение между длинной проволоки и ее массой
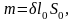
где
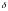 - плотность меди;
- плотность меди;
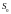 - площадь сечения проволоки.
- площадь сечения проволоки.
Выразим
через
известные параметры
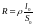
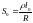 ,
,
где
- удельное сопротивление меди.
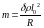 .
.
Таким образом,
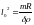 и
и
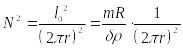 .
.
Подставим
найденное значение
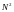 в исходную формулу
в исходную формулу

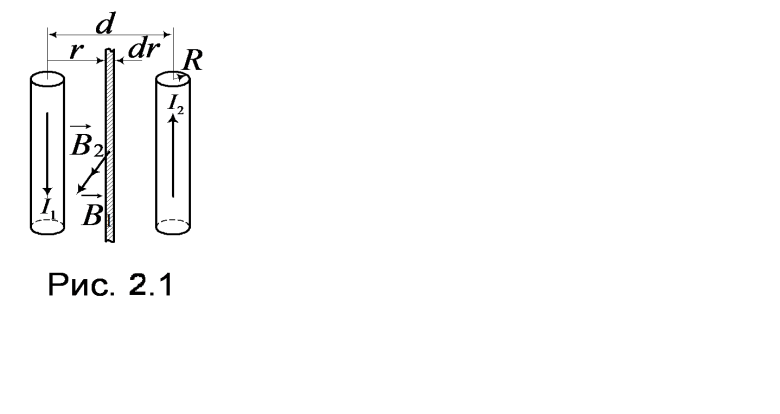
4. Определить индуктивность L двухпроводной линии на участке длиной l. Радиус провода R. Расстояние между осевыми линиями d.
Решение
Магнитный поток через элементарную площадку шириной dr ( рис.2.1) равен
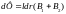 ,
,
где
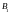 и
и
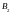 - индукции магнитного поля, создаваемые
проводниками с токами
- индукции магнитного поля, создаваемые
проводниками с токами
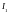 и
и
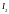 ,
соответственно. Полный поток
,
соответственно. Полный поток
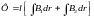 .
Из соображений симметрии
.
Из соображений симметрии
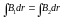 и
и
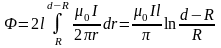 .
.
Индуктивность
двухпроводной линии
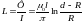 .
.
5.
Вычислить взаимную индуктивность
длинного прямого провода и квадратной
рамки со стороной а. Рамка и прямой
провод лежат в одной плоскости, причем
центр рамки отстоит от провода на
расстоянии
![]() .
.
Решение
Элементарный поток через узкую полоску рамки dx, отстоящую на расстоянии x от прямолинейного проводника
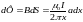 .
Поток через всю рамку
.
Поток через всю рамку
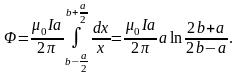
Коэффициент
взаимной индуктивности
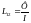 ,
,
где I – ток, текущий по прямолинейному проводнику.
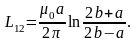
6. Определить взаимную индуктивность тороидальной катушки и проходящего по ее оси бесконечного прямого провода. Катушка имеет прямоугольное сечение, ее внутренний радиус , внешний b. Длина стороны поперечного сечения тора, параллельная проводу, равна h. Число витков катушки N. Магнитную проницаемость всюду считать равной единице.
Решение
Как
и в предыдущей задаче элементарный
магнитный поток через элемент сечения
тороида
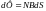 ,
,
где В – индукция поля, создаваемого прямолинейным провод-ником на расстоянии х, dS- элемент сечения тороида.
Поток через сечение тороида
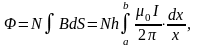
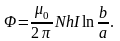
Так как ,
где I – ток в прямолинейном проводнике, то
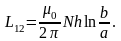
7. На тороидальную катушку намотаны
две вплотную прилегающие друг к другу
системы обмоток с полными числами витков
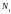 и
и
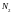 .
Считая радиус одного витка обмотки
равным r и радиус тора –
R(r
.
Считая радиус одного витка обмотки
равным r и радиус тора –
R(r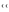 R),
найти коэффициент взаимной индукции
катушки.
R),
найти коэффициент взаимной индукции
катушки.
Решение
Магнитное
поле, создаваемое одной катушкой внутри
тора, равно
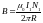 ,
,
где
- ток в обмотке первой катушки. Магнитный
поток через все витки второй катушки
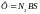 ,
,
где S – площадь поперечного сечения тора.
Так
как, с другой стороны, известно, что
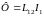 ,
то
,
то
коэффициент взаимоиндукции равен
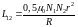 .
.
8. Две катушки, индуктивности которых
равны
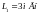 и
и
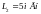 ,
соединены последовательно так, что их
магнитные поля направлены в одну сторону;
при этом индуктивность всей системы
оказалась равной 11мГн. Найти
индуктивность системы
,
соединены последовательно так, что их
магнитные поля направлены в одну сторону;
при этом индуктивность всей системы
оказалась равной 11мГн. Найти
индуктивность системы
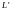 ,
если катушки переключить так, чтобы их
поля были направлены навстречу друг
другу. Взаимное расположение катушек
при этом не меняется.
,
если катушки переключить так, чтобы их
поля были направлены навстречу друг
другу. Взаимное расположение катушек
при этом не меняется.
Решение
И ндуктивность
системы определяется суммарным потоком
сцепления. Первая катушка пронизывается
собственным потоком
ндуктивность
системы определяется суммарным потоком
сцепления. Первая катушка пронизывается
собственным потоком
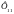 и потоком
и потоком
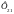 ,
создаваемым второй катушкой. Вторая
катушка пронизывается также собственным
потоком
,
создаваемым второй катушкой. Вторая
катушка пронизывается также собственным
потоком
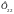 и потоком
и потоком
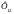 ,
созданным первой катушкой. До переключения
катушек их поля направлены в одну сторону
(рис. 2.2а) и потоки складываются
,
созданным первой катушкой. До переключения
катушек их поля направлены в одну сторону
(рис. 2.2а) и потоки складываются
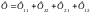 .
.
После переключения катушек (рис. 2.2б) суммарный поток
сцепления
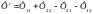 .
.
Знаки «минус» показывают, что поле первой катушки направлено навстречу собственному полю второй катушки. Тоже самое можно сказать и о потоке, созданном второй катушкой и пронизывающем первую.
Потоки
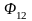 и
и
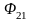 в данном случае равны друг другу, так
как катушки соединены последовательно
и, следовательно, обтекаются одинаковым
током, т.е.
в данном случае равны друг другу, так
как катушки соединены последовательно
и, следовательно, обтекаются одинаковым
током, т.е.
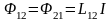 ,
,
где
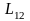 - коэффициент взаимной индукции.
- коэффициент взаимной индукции.
Собственные потоки могут быть выражены через индуктивности каждой из катушек
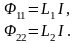
Подставляя полученные выражения в формулу для суммарных потоков, получим
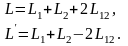
Совместное решение этих уравнений даёт результат
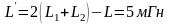 .
.
9. Соленоид с индуктивностью
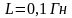 и сопротивлением
и сопротивлением
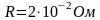 замыкают на источник ЭДС
замыкают на источник ЭДС
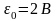 ,
внутреннее сопротивление которого
ничтожно мало. Какое количество
электричества пройдёт через соленоид
за первые 5 секунд после замыкания?
,
внутреннее сопротивление которого
ничтожно мало. Какое количество
электричества пройдёт через соленоид
за первые 5 секунд после замыкания?
Решение
При замыкании соленоида на ЭДС
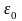 возникает переменный экстраток замыкания,
вследствие явления самоиндукции.
Элементарное количество электричества,
которое пройдёт через соленоид за
промежуток времени
возникает переменный экстраток замыкания,
вследствие явления самоиндукции.
Элементарное количество электричества,
которое пройдёт через соленоид за
промежуток времени
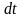
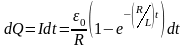 .
.
Отсюда находим количество электричества
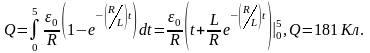
1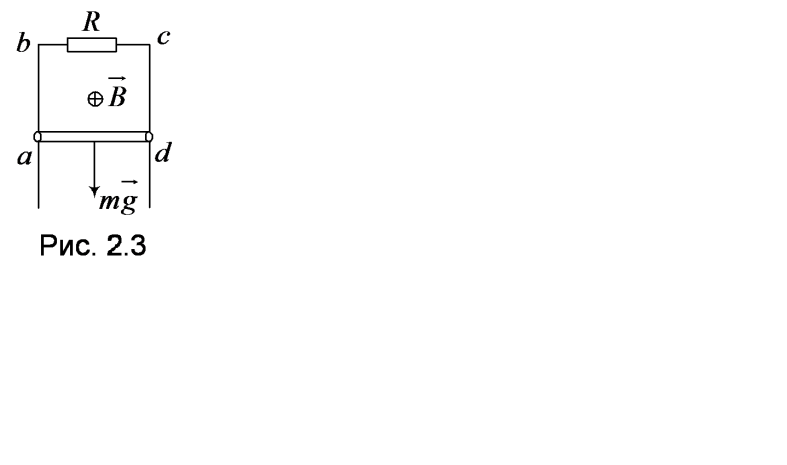 0.
Резистор сопротивлением
присоединён
к верхним концам двух вертикальных
медных стержней, отстоящих на расстоянии
0.
Резистор сопротивлением
присоединён
к верхним концам двух вертикальных
медных стержней, отстоящих на расстоянии
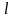 друг от друга (рис. 2.3). Стержни замкнуты
медной перемычкой массой
,
которая без трения может скользить по
ним. В окружающем пространстве создано
однородное магнитное поле с индукцией
,
перпендикулярное плоскости, в которой
расположены стержни. Перемычку опустили,
после чего она начала падать без нарушения
электрического контакта. Пренебрегая
сопротивлением стержней и перемычки,
найти установившуюся скорость
последней. Принять индуктивность единицы
длины системы стержней равной
друг от друга (рис. 2.3). Стержни замкнуты
медной перемычкой массой
,
которая без трения может скользить по
ним. В окружающем пространстве создано
однородное магнитное поле с индукцией
,
перпендикулярное плоскости, в которой
расположены стержни. Перемычку опустили,
после чего она начала падать без нарушения
электрического контакта. Пренебрегая
сопротивлением стержней и перемычки,
найти установившуюся скорость
последней. Принять индуктивность единицы
длины системы стержней равной
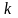 .
.
Решение
При падении перемычки площадь контура
а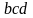 растёт и магнитный поток сквозь него
увеличивается. Согласно закону Фарадея,
в контуре появляется ЭДС индукции,
вызывающая индукционный ток. Следовательно,
на перемычку
растёт и магнитный поток сквозь него
увеличивается. Согласно закону Фарадея,
в контуре появляется ЭДС индукции,
вызывающая индукционный ток. Следовательно,
на перемычку
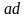 кроме силы тяжести
кроме силы тяжести
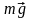 действует со стороны магнитного поля
сила Ампера
действует со стороны магнитного поля
сила Ампера
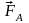 .
Так как для всех элементов перемычки
.
Так как для всех элементов перемычки
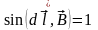 и
и
![]() ,
то
,
то
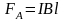 .
.
Согласно правилу Ленца, индукционный
ток направлен против часовой стрелки
и, сила
направлена против силы
.
С ростом скорости падения перемычки
увеличивается ЭДС индукции, сила тока
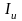 ,
следовательно, сила Ампера
,
следовательно, сила Ампера
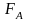 .
Скорость перестаёт возрастать, когда
наступает равновесие между
и
,
т.е.
.
Скорость перестаёт возрастать, когда
наступает равновесие между
и
,
т.е.
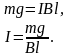
По закону Ома для замкнутой цепи I=ε/R,
где ε – ЭДС, действующая в контуре abcd и равная сумме
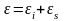 .
.
Величина
- ЭДС индукции, возникающая при изменении
сквозь контур магнитного потока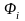 вектора
.
Абсолютное значение
равно
вектора
.
Абсолютное значение
равно
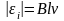 .
.
Величина
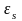 - ЭДС самоиндукции. Она появляется при
изменении сквозь контур
- ЭДС самоиндукции. Она появляется при
изменении сквозь контур
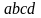 магнитного потока
магнитного потока
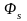 ,
созданного индукционным током.
,
созданного индукционным током.
При определении необходимо учитывать, что индуктивность контура – величина переменная
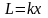 ,
,
где
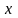 - длина вертикальных стержней, измеренная
на участке, по которому идёт ток. При
движении перемычки, величины
и
- длина вертикальных стержней, измеренная
на участке, по которому идёт ток. При
движении перемычки, величины
и
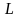 возрастают.
возрастают.
Таким образом, ЭДС самоиндукции
![]() .
.
Так как при установившейся скорости
падения перемычки
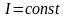 и
и
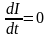 ,
то
,
то
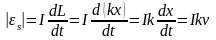 .
.
Величины и имеют в данном случае противоположные знаки, поскольку соответствующие им магнитные потоки и направлены согласно правилу Ленца, противоположно (при этом оба потока растут по абсолютной величине). Учитывая это, найдём
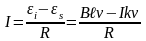 .
.
Подставив найденное значение
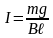 ,
получим
,
получим
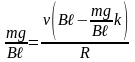 ,
,
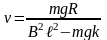 .
.
Задачи для самостоятельного решения
1. По катушке индуктивностью L=0,03мГн течет ток
I=0,6А.
При размыкании цепи сила тока изменяется
практически до нуля за время
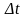 =
120 мкс.
Определить среднюю ЭДС самоиндукции
=
120 мкс.
Определить среднюю ЭДС самоиндукции
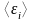 ,
возникающую в контуре.
,
возникающую в контуре.
Ответ:
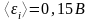
2. С
помощью реостата равномерно увеличивают
силу тока в катушке на
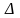 I=0,1А
в 1с.
Индуктивность L
катушки равна 0,01Гн.
Найти среднее значение ЭДС самоиндукции
.
I=0,1А
в 1с.
Индуктивность L
катушки равна 0,01Гн.
Найти среднее значение ЭДС самоиндукции
.
Ответ:
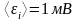
3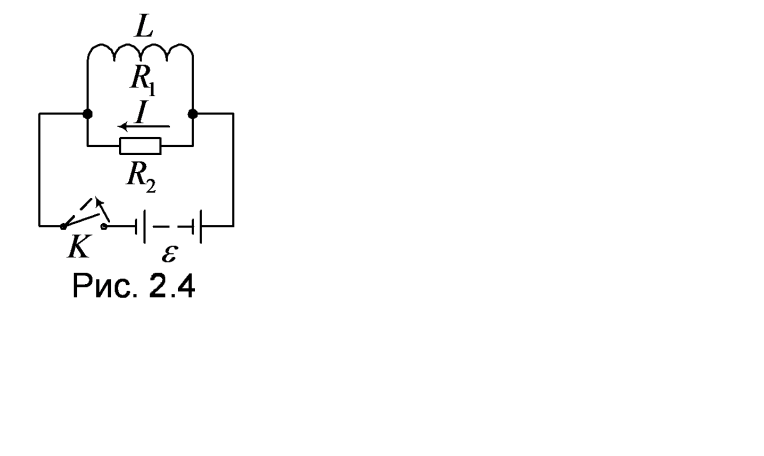 .
Индуктивность L
катушки равна 2
мГн.
Ток частотой
.
Индуктивность L
катушки равна 2
мГн.
Ток частотой
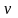 =50
Гц,
протекающий по катушке, изменяется по
синусоидальному закону. Определить
среднюю ЭДС самоиндукции
возникающую за интервал времени
t,
в течение которого
ток в катушке изменяется от минимального
до максимального значения. Амплитудное
значение силы тока
=10
А.
=50
Гц,
протекающий по катушке, изменяется по
синусоидальному закону. Определить
среднюю ЭДС самоиндукции
возникающую за интервал времени
t,
в течение которого
ток в катушке изменяется от минимального
до максимального значения. Амплитудное
значение силы тока
=10
А.
Ответ:
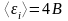
4. Катушка
сопротивлением
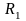 =0,5Ом
с индуктивностью L=4мГн
соединена параллельно с проводом
сопротивлением
=0,5Ом
с индуктивностью L=4мГн
соединена параллельно с проводом
сопротивлением
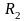 =2,5Ом,
по которому течет постоянный ток I=1А.
Определить количество электричества
Q,
которое будет индуцировано в катушке
при размыкании цепи ключом К
(рис. 2.4).
=2,5Ом,
по которому течет постоянный ток I=1А.
Определить количество электричества
Q,
которое будет индуцировано в катушке
при размыкании цепи ключом К
(рис. 2.4).
Ответ:
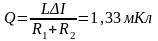
5. На картонный каркас длиной = 50 см и площадью S сечения, равной 4 см2, намотан в один слой провод диаметром d=0,2мм так, что витки плотно прилегают друг к другу (толщиной изоляции пренебречь). Вычислить индуктивность L получившегося соленоида.
Ответ:
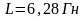
6. Индуктивность L соленоида длиной =1 м, намотанного в одни слой на немагнитный каркас, равна 1,6 мГн. Площадь S сечения соленоида равна 20 см2. Определить число п витков на каждом сантиметре длины соленоида.
Ответ:

7. Сколько
витков проволоки диаметром
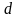 =0,4мм
с изоляцией ничтожной толщины нужно
намотать на картонный цилиндр диаметром
D=2
см,
чтобы получить однослойную катушку с
индуктивностью L=1
мГн?
Витки вплотную прилегают друг к другу.
=0,4мм
с изоляцией ничтожной толщины нужно
намотать на картонный цилиндр диаметром
D=2
см,
чтобы получить однослойную катушку с
индуктивностью L=1
мГн?
Витки вплотную прилегают друг к другу.
Ответ:
8. Катушка, намотанная на немагнитный цилиндрический
каркас, имеет
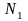 =750
витков и индуктивность L1=25
мГн.
Чтобы увеличить индуктивность катушки
до L2=36
мГн,
обмотку с катушки сняли и заменили
обмоткой из более тонкой проволоки с
таким расчетом, чтобы длина катушки
осталась прежней. Определить число
N2
витков катушки
после перемотки.
=750
витков и индуктивность L1=25
мГн.
Чтобы увеличить индуктивность катушки
до L2=36
мГн,
обмотку с катушки сняли и заменили
обмоткой из более тонкой проволоки с
таким расчетом, чтобы длина катушки
осталась прежней. Определить число
N2
витков катушки
после перемотки.
Ответ:
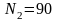
9. Соленоид содержит N=1000 витков. Площадь S сечения
сердечника равна 10 см2. По обмотке течет ток, создающий поле с индукцией В=1,5 Тл. Найти среднюю ЭДС индукции , возникающей в соленоиде, если ток уменьшится до нуля за время t= 500 мкс.
Ответ:
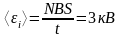
10. Две
катушки расположены на небольшом
расстоянии одна от
другой. Когда сила тока в первой катушке
изменяется с быстротой:
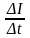 = 5 А/с,
во второй катушке возникает ЭДС индукции
=0,1
В.
Определить коэффициент
взаимной индукции катушек.
= 5 А/с,
во второй катушке возникает ЭДС индукции
=0,1
В.
Определить коэффициент
взаимной индукции катушек.
Ответ:
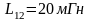
11. Обмотка тороида с немагнитным сердечником имеет
N1=251
виток. Средний диаметр
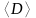 тороида равен 8 см,
диаметр d
витков равен 2 см.
На тороид намотана вторичная обмотка,
имеющая N2=
100 витков. При замыкании первичной
обмотки в ней в течение
t=1
мс
устанавливается сила тока
тороида равен 8 см,
диаметр d
витков равен 2 см.
На тороид намотана вторичная обмотка,
имеющая N2=
100 витков. При замыкании первичной
обмотки в ней в течение
t=1
мс
устанавливается сила тока
I=3 А. Найти среднюю ЭДС индукции , возникающей на вторичной обмотке.
Ответ:
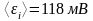
12. В цепи шел ток I0=50А. Источник тока можно отключить от цепи, не разрывая ее. Определить силу тока в этой цепи через t=0,01с после отключения ее от источника тока. Сопротивление R цепи равно 20Ом, ее индуктивность L=0,1Гн.
Ответ: I=6,75А.
13. Источник тока замкнули на катушку с сопротивлением R=10Ом и индуктивностью L=1 Гн. Через сколько времени сила тока замыкания достигнет 0,9 предельного значения?
Ответ: t=0,23с
14. Цепь состоит из катушки индуктивностью L =1Гн и сопротивления R=10 Ом. Источник тока можно отключать, не разрывая цепи. Определить время t, по истечении которого сила тока уменьшится до 0,001 первоначального значения.
Ответ: t=0,69с
