Электромагнитная индукция Основные законы и формулы
Основной закон электромагнитной индукции (закон Фарадея)
,
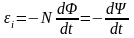где
-
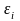электродвижущая сила индукции, N
- число витков контура,
-
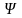потокосцепление.
Частные случаи применения основного закона электромагнитной индукции:
а) разность потенциалов U на концах проводника длиной
,
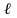движущегося со скоростью v
в однородном магнитном поле
,
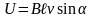где
-
угол между направлениями вектора
скорости и вектора магнитной индукции;
б) электродвижущая сила индукции
,
возникающая в рамке, содержащей N
витков площадью S, при
вращении рамки с угловой скоростью
,
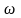в однородном магнитном поле с индукцией
,
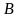
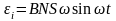где
-
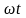мгновенное значение угла между вектором
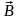и вектором нормали
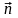к плоскости рамки.
Количество электричества Q, протекающего в контуре
,
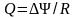где R – сопротивление
контура,
-
изменение потокосцеп-ления.
Мгновенное значение силы тока
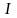в цепи, обладающей активным сопротивлением
R и индуктивностью
L:
а) после замыкания цепи
,
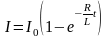где
-
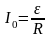установившийся ток (при
);
-
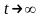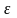ЭДС источника t –
время, прошедшее после замыкания цепи;
б) после размыкания цепи
,
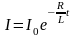где
-
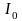сила тока в цепи при t=0;
t – время, прошедшее
после размыкания цепи.
Примеры решения задач
1
.
В плоскости квадратной рамки с
сопротивлением R=7Ом
и стороной
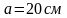расположен на расстоянии
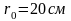от
рамки прямой бесконечный проводник
(рис.1.1). Сила тока в проводнике изменяется
по закону
,
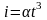где
.
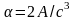Проводник параллелен одной из сторон
рамки. Определить силу тока в рамке в
момент времени
.
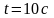Решение
Элементарный магнитный поток сквозь узкую полоску
.
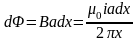Интегрируя это выражение по x
в пределах от
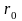до
,
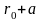находим
.
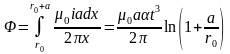По закону Фарадея определим ЭДС индукции
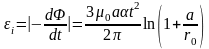
и силу тока
,
.
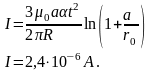2. Квадратная рамка со стороной
a=20см удаляется
от бесконечного проводника со скоростью
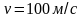в направлении перпендикулярном
проводнику. По проводнику течёт постоянный
ток
.
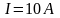Определить ЭДС индукции в рамке через
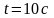от начала движения,
если в начальный момент времени рамка
находилась на расстоянии
от проводника.
Решение
Найдём элементарный поток сквозь узкую полосу (рис.1.1)
,
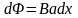где
,
а
.
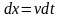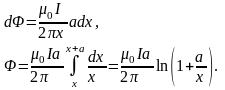
Для
,
.
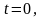
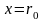
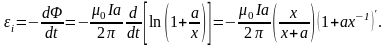
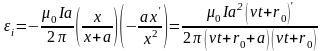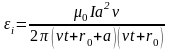Производя вычисления, можно учесть, что
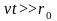и
.
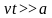При
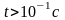величинами
и
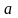можно пренебречь и
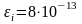В.
3
.
Длинный прямой проводник с током I
и П-образный проводник с подвижной
перемычкой расположены в одной плоскости
(рис.1.2). Перемычку, длина которой
перемещают вправо с постоянной скоростью
.
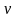Найти ЭДС индукции в контуре, как функцию
расстояния
.
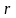Решение
Как и в предыдущей задаче найдём элементарный поток через узкую полоску и весь контур
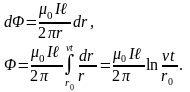
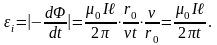
Учитывая, что движение перемычки
происходит с постоянной скоростью
.
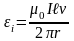И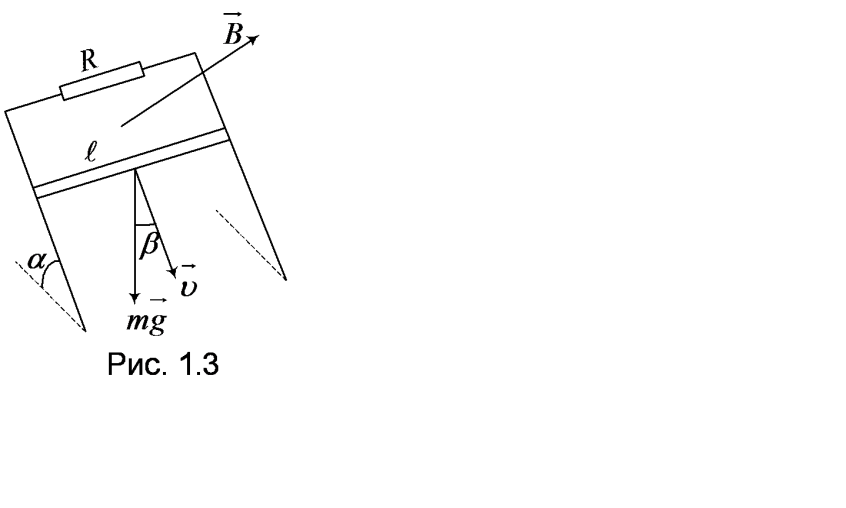
ндукционный
ток в рамке
.
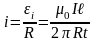4. По двум гладким медным шинам,
установленным под углом
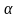к горизонту, скользит под действием
силы тяжести медная перемычка массой
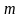(рис.1.3).
Шины замкнуты на сопротивление
.
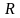Расстояние между шинами
.
Система находится в однородном магнитном
поле с индукцией
,
перпендикулярном к плоскости, в которой
перемещается перемычка. Сопротивление
шин, перемычки и скользящих контактов,
а также самоиндукция контура пренебрежимо
малы. Найти установившуюся скорость
перемычки.
Решение
Изменение магнитного потока через контур обусловлено движением перемычки. Так как магнитное поле однородно, то
.
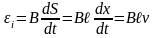На перемычку действует две силы: сила
тяжести
и сила Ампера
.
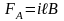По второму закону Ньютона
,
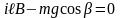где
-
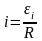индукционный ток в контуре.
Угол
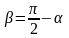и
.
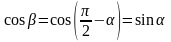Таким образом,
,
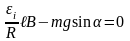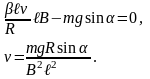
5. Система отличается от рассмотренной
в предыдущей задаче (рис.1.3) лишь тем,
что вместо сопротивления
к концам шин подключен конденсатор
ёмкости
.
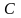Найти ускорение перемычки.
Решение
Как и в предыдущей задаче, изменение
магнитного потока через контур обусловлено
движением перемычки. По закону Ома для
неоднородного участка ЭДС индукции
в любой момент времени равна разности
потенциалов
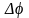на обкладках конденсатора
.
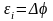Так как
,
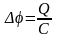то индукционный ток в контуре
,
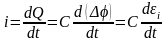где
.
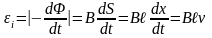Таким образом,
,
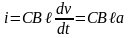где - искомое ускорение перемычки.
На перемычку действуют две силы: сила
тяжести
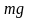и сила Ампера
.
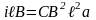По второму закону Ньютона
,
где
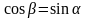(см. задачу 4).
Следовательно
.
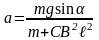Если на перемычку действует сила трения, то
,
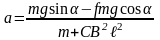где
-
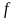коэффициент трения.
6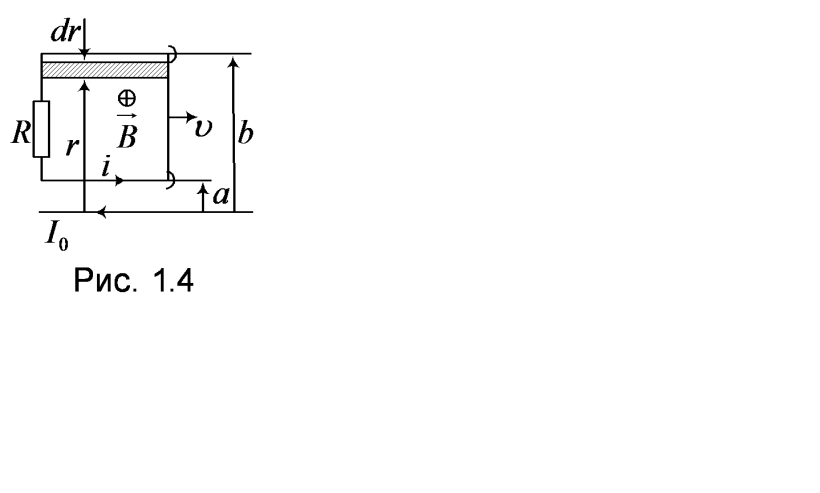
.
На расстояниях
и
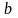от длинного прямого проводника с
постоянным током
расположены два параллельных ему
провода, замкнутых на одном конце
сопротивлением
(рис.1.4). По проводам без трения перемещают
с постоянной скоростью
стержень-перемычку. Пренебрегая
сопротивлением проводов, стержня и
скользящих контактов, а также индуктивностью
контура, найти:
а) значение и направление индуктивного тока в стержне;
б) силу, необходимую для поддержания постоянства скорости.
Решение
Магнитный поток, создаваемый током
,
сквозь замкнутый контур направлен от
нас (рис.1.4). Кроме того, он увеличивается,
так как перемычка движется вправо.
Следовательно, согласно правилу Ленца,
индукционный ток в контуре
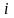направлен против часовой стрелки.
Магнитный поток сквозь контур
,
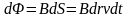где
.
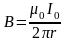Таким образом,
.
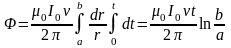Возникающая в контуре ЭДС индукции
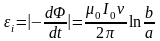
и индукционный ток
.
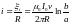Для поддержания постоянства скорости движения перемычки, к ней необходимо приложить силу равную силе Ампера и направленную в противоположную сторону (согласно второму закону Ньютона).
,
,
.
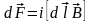
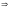
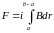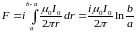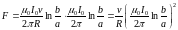7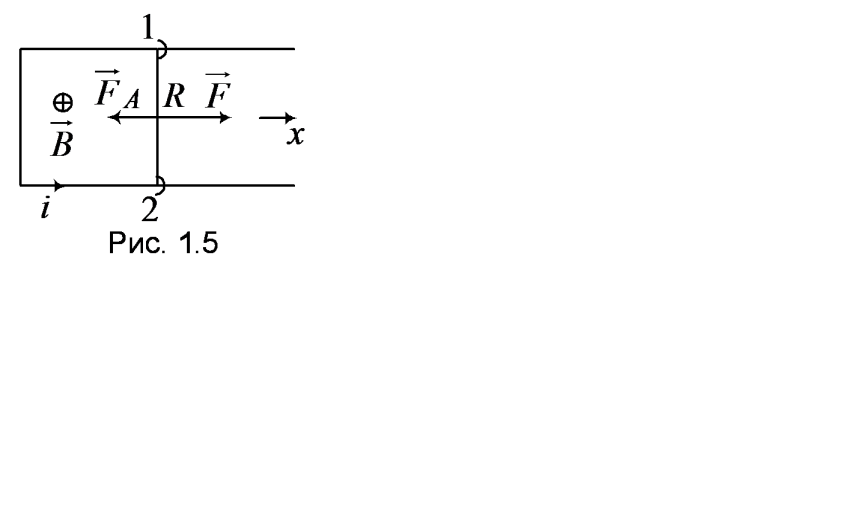
.
По П-образному проводнику, расположенному
в горизонтальной плоскости, может
скользить без трения перемычка 12
(рис.1.5). Последняя имеет длину l,
массу m и сопротивление
R. Вся система находится
в однородном магнитном поле с индукцией
В. В момент t=0
на перемычку стали действовать с
постоянной горизонтальной силой F,
и перемычка начала перемещаться вправо.
Найти зависимость скорости перемычки
от t. Самоиндукция
и сопротивление П-образного проводника
пренебрежимо малы.
Решение
При движении перемычки вправо магнитный
поток сквозь контур возрастает, что
приводит к возникновению э.д.с. индукции
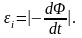
Индукционный ток
согласно правилу Ленца направлен против
часовой стрелки (рис.1.5).
Очевидно, что сила Ампера, действующая
на перемычку
,
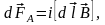направлена противоположно приложенной
силе
.
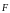Таким образом, уравнение движения
перемычки согласно второму закону
Ньютона
,
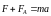где
,
.
.
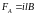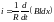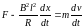
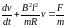Таким образом, мы получили неоднородное
дифференциальное уравнение, общее
решение которого будем искать в виде
суммы общего решения соответствующего
однородного уравнения и частного решения
неоднородного уравнения
.
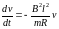Введем обозначения
,
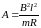тогда
,
.
.
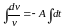
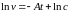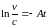
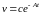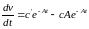Подставим в дифференциальное уравнение
.
.
.
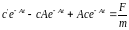
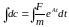
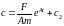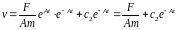Пр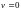и
,
и
.
Следовательно
.
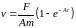При
,
,
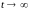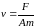где
.
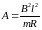8
.
Квадратная проволочная рамка со стороной
и прямой проводник с постоянным током
I лежат в одной плоскости
(рис.1.6). Сопротивление рамки R.
Её повернули на 180̊
вокруг оси
,
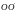отстоящей от проводника с током на
расстояние b. Найти
количество электричества, протекшее в
рамке.
Решение
Поворот рамки приводит к изменению магнитного потока через нее и, как следствие, возникновению ЭДС индукции. Таким образом, заряд прошедший по рамке
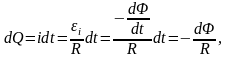
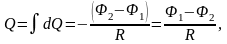
где
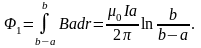
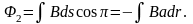
Так как нормаль к контуру изменила свое направление на 180̊, то
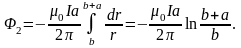
Таким образом,
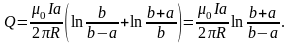
9. Плоская спираль с очень большим
числом витков N, плотно
прилегающих друг к другу, находится в
однородном магнитном поле, перпендикулярном
к плоскости спирали. Наружный радиус
витков спирали равен
.
Индукция поля изменяется во времени по
закону
,
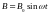где
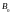и ω - постоянные. Найти амплитудное
значение ЭДС индукции в спирали.
Решение
ЭДС индукции в спирали
,
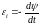где
.
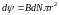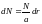- число витков спирали в интервале
значений радиуса dr.
Таким образом,
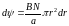и
.
.
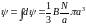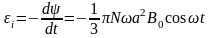Амплитудное значение ЭДС индукции
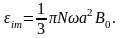
10. На длинный прямой соленоид, имеющий
диаметр сечения d=5см
и содержащий n=20
витков на один сантиметр длины, плотно
надет круговой виток из медного провода
сечением
.
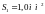Найти ток i в витке,
если ток в обмотке соленоида увеличивают
с постоянной скоростью
.
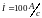Решение
ЭДС индукции наводимое в кольце
где
,
S – площадь сечения
соленоида.
Таким образом,
Индукционный ток найдем из соотношения
,
где
,
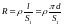где
- удельное сопротивление меди,
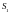- площадь витка.
.
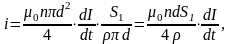
11. Внутри длинного соленоида находится
катушка из N витков с
площадью поперечного сечения S.
Катушку поворачивают с постоянной
угловой скоростью
вокруг оси, совпадающей с ее диаметром
и перпендикулярной к оси соленоида.
Найти ЭДС индукции в катушке, если
индукция магнитного поля в соленоиде
меняется со временем как
и в момент t=0 ось
катушки совпадала с осью соленоида.
Решение
В момент времени t
полный магнитный поток сквозь катушку
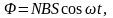
где - угол между нормалью к катушке и осью соленоида.
.
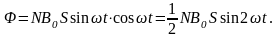Согласно закону электромагнитной индукции.
