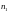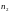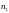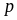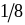Занятие № 11-12. Функции случайных величин

Если X - дискретная СВ, имеющая закон распределения (х_k, р_k) k=1, 2,..., который можно записать в виде табл.1, и Y= (Х), где -неслучайная функция, то Y также является дискретной CВ, причем ее возможные значения у_k= (х_k).

Таблица 1

X	x1	x2	x3	…	xk	…
P(X)	p1	p2	p3	…	pk	…

Если (х) – монотонная функция, то все значения y_k различны и P(Y=y_k)=P(X=x_k), то есть СВ Y имеет следующий закон распределения (табл.2)

Таблица 2

Y	(x1)	(x2)	…	(xk)	…
P(Y)	p1	p2	…	pk	…

Если при этом (х) – немонотонная функция, то среди

ее значений у₁,у₂,у₃,…,у_k,… могут быть одинаковые. В этом случае столбцы с равными значениями (х_i) объединяются в один столбец, а соответствующие вероятности складываются, т. е.

.

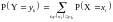Если Х – непрерывная СВ с ФР F(x) и плотностью вероятности f(x) и Y= (х), причем (х) – монотонно возрастающая непрерывно дифференцируемая функция, а х= ^-1(у) – обратная функция, то

F(y)=P(Y<y)=P( (х)<y)=P(X< ^-1(х))=F[ ^-1(х)].

Дифференцируя последнее равенство по у, получаем

или .

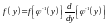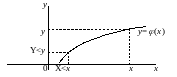
Если у=φ(х) - монотонно убывающая функция, то аналогично получаются следующие соотношения:

F(y)=1-F[φ^-1(y)], f(y)= -f[φ^-1(y)]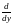 [φ^-1(y)].

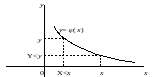
Выражения для плотности вероятности СB Y и для

монотонно возрастающей и для монотонно убывающей функции φ(х) можно объединить:

.

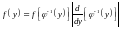Рассмотрим непрерывную случайную величину с плотностью распределения и случайную величину 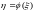с плотностью распределения . По определению функция

распределения 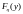случайной величины равна

.

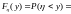
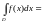
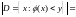
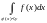Числовые характеристики находятся по формулам:

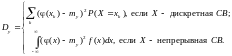
Для случайного вектора с плотностью распределения если , то

Пример 1. Найти закон распределения СB. Y=(Х-т)/σ, если СВ X подчиняется нормальному закону N(m,σ).

Решение. В нашем случае Y=(1/σ)Х-т/σ, т.е. а=1/σ, b=-т/σ. Вспоминая формулу для плотности распределения нормального закона N(m,σ) и учитывая формулу (3), получаем

,

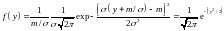т.е. СВ Y распределена по закону N(0,1).

Отсюда

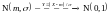
Пример 2. Логарифмически нормальное распределение.

CB X распределена нормально по закону N(m,σ). Найти плотность распределения СB Y== (Х); 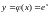отсюда и следовательно,

.

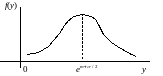
Функция е^х – монотонно возрастающая всюду, поэтому находим .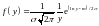

, .

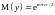Пример 3. Распределение Пирсона 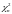с степенями свободы. Пусть 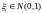и независимы. Тогда

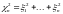
имеет плотность распределения

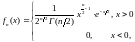
где 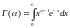– Гамма-функция. ,

.

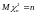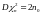Пример 4. Распределение Стьюдента с степенями свободы 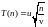, где 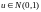, , – независимые случайные величины, имеет плотность распределения

.

, , .

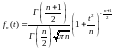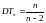Пример 5. Плотность распределения случайной величины равна . Найти плотность распределения случайной величины

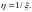
Решение. Решение задачи располагаем в виде двух столбцов; слева будем писать обозначения функций, принятые в общем случае; справа – конкретные функции, соответствующие данному примеру:

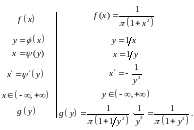
Пример 6. Бросаются 3 монеты. Пусть 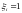, если 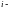ая монета выпала орлом вверх и 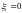в противном случае, 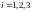. Построить ряд распределения случайной величины .

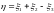Решение.

1. Определяем пространство элементарных исходов.

Элементарными исходами рассматриваемого случайного эксперимента являются упорядоченные наборы чисел 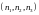, где 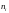либо нуль, либо единица .

2. Определяем множество возможных значений .

Случайная величина на элементарном исходе (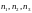 ) принимает значение .

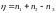3. Составляем таблицу элементарных исходов и соответствующих им значений .

	0	1	0	0	1	1	0	1
	0	0	1	0	1	0	1	1
	0	0	0	1	0	1	1	1
	0	1	1	–1	2	0	0	1

4. Определяем вероятности значений и строим ее ряд распределения. Всего элементарных исходов 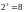. Следовательно, вероятность элементарного исхода равна . Имеем

	–1	0	1	2