
- •Часть 2
- •Справочный материал и принципы решения задач Занятие № 6. Законы распределения и числовые характеристики случайных величин
- •Примеры дискретных распределений
- •Примеры непрерывных распределений
- •Примеры для самостоятельного решения.
- •Занятие № 7. Нахождение числовых характеристик дискретных случайных величин, принимающих целочисленные значения методом производящей функции. Распределение Пуассона. Нормальное распределение.
- •Простейшие свойства интеграла вероятностей
- •Занятия № 8-10. Многомерные случайные величины (случайные векторы).
- •Свойства функции и плотности распределения вероятности
- •Теорема умножения плотностей
- •Занятие № 11-12. Функции случайных величин
- •Примеры для самостоятельного решения.
- •Занятие № 13. Центральная предельная теорема и следствия из нее. Закон больших чисел. Неравенство Чебышева
- •Теорема Чебышева
- •Часть 2
- •394026 Воронеж, Московский просп., 14
Занятия № 8-10. Многомерные случайные величины (случайные векторы).
Вектор
 ,
координаты которого есть случайные
величины, заданные на одном и том же
вероятностном пространстве, называется
случайным
вектором,
а функция
,
координаты которого есть случайные
величины, заданные на одном и том же
вероятностном пространстве, называется
случайным
вектором,
а функция
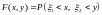 называется функцией распределения
называется функцией распределения
случайного
вектора
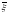 или двумерной случайной величины
.
или двумерной случайной величины
.
Если координаты вектора дискретные случайные величины, то называют дискретным случайным вектором.
Законом
распределения дискретного случайного
вектора называется перечень всех
возможных значений пар компонент
{(xi,yj)|(xi,yj)
G(x,y)} и соответствующих
каждой паре вероятностей pij=P(X=xi,Y=уj),
удовлетворяющих условию где суммирование распространяется на
все возможные значения индексов i
и j.
где суммирование распространяется на
все возможные значения индексов i
и j.
Закон распределения двумерного случайного вектора часто задается таблицей вида
X Y |
x1 |
x2 |
… |
xi |
… |
y1 |
p11 |
p21 |
… |
pi1 |
… |
y2 |
p12 |
p22 |
… |
pi2 |
… |
… |
… |
… |
… |
… |
… |
yj |
p1j |
p2j |
… |
pij |
|
… |
… |
… |
… |
… |
… |
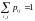
Зная закон распределения двумерного случайного вектора, можно получить закон распределения его компонент
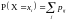 ,
,
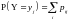 и ФР
и ФР
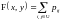 ,
,
где множество индексов U определяется следующим образом:
U={(i,j)|(X<xi, Y<yj)}.
Если
функцию распределения вероятности
вектора
можно представить в виде
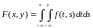 ,
то случайную величину
,
то случайную величину
 называют непрерывной
двумерной случайной величиной,
а
называют непрерывной
двумерной случайной величиной,
а
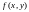 – ее плотностью
распределения вероятности.
– ее плотностью
распределения вероятности.
Всюду в дальнейшем будем считать, что – непрерывная функция по обоим аргументам.
Свойства функции и плотности распределения вероятности
1)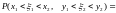

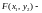

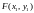 .
.
2)
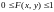 .
.
3)
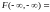
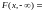
 0.
0.
4)
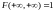 .
.
5)
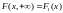 ,
, 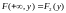 ,
где
,
где
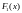 и
и
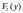 – функции распределения случайных
величин
– функции распределения случайных
величин
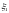 и
и
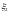 .
.
6)
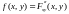 .
.
7)
 .
.
8)
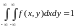 .
.
9)
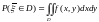 .
.
10)
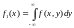 ,
,
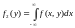 ,
,
где
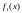 и
и
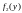 – плотности распределения случайных
величин
и
.
– плотности распределения случайных
величин
и
.
Условной
плотностью распределения случайной
величины
при условии
 называют отношение плотности совместного
распределения
называют отношение плотности совместного
распределения
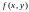 системы (
,
)
к плотности распределения составляющей
:
системы (
,
)
к плотности распределения составляющей
:
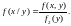
Аналогично
определяют
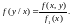
Теорема умножения плотностей
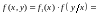
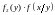 .
.
Случайные
величины
и
называются независимыми,
если для любых чисел x,y
случайные события
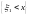 и
и
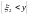 независимы.
независимы.
Случайные события независимы, если выполняется любое из условий:
1)
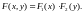
2)
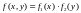 .
.
3)
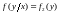 или
или
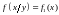 .
.
Условным математическим ожиданием называют выражение
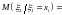
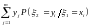 для
дискретного случайного вектора
для
дискретного случайного вектора

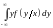 для
непрерывного случайного вектора.
для
непрерывного случайного вектора.
Величина
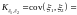
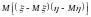 называется корреляционным
моментом (ковариацией)
двух случайных величин
и
.
называется корреляционным
моментом (ковариацией)
двух случайных величин
и
.
Если
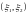 – непрерывная двумерная случайная
величина с плотностью распределения
,
то
– непрерывная двумерная случайная
величина с плотностью распределения
,
то
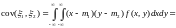
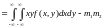 ,
,
где
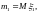
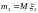 .
.
Для дискретного случайного вектора

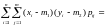
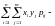
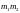 .
.
Величина
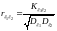 называется коэффициентом корреляции
случайных величин
и
.
называется коэффициентом корреляции
случайных величин
и
.
Если
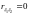 ,
то случайные величины
и
называются некоррелированными.
,
то случайные величины
и
называются некоррелированными.
Свойства корреляционного момента и коэффициента
корреляции
1)
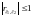 .
.
2)
Если
и
независимы, то
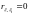 .
Обратное неверно: из некоррелируемости
случайных величин не следует их
независимость.
.
Обратное неверно: из некоррелируемости
случайных величин не следует их
независимость.
3)
Если
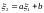 ,
то
,
то
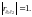
4)
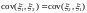 .
.
5)
 .
.
6)
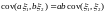 .
.
7)
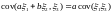
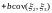 .
.
Свойства математического ожидания и дисперсии
случайного вектора
1)
 ,
где
,
где
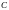 – постоянная.
– постоянная.
2)
 .
.
3)
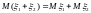 .
.
4)
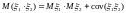 .
.
Если
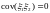 ,
то
,
то
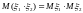 .
.
Случайная
величина
называется неотрицательной
 ,
если она принимает только неотрицательные
значения.
,
если она принимает только неотрицательные
значения.
5)
Если
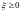 ,
,
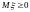 .
.
6)
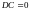 ,
где С – постоянная.
,
где С – постоянная.
7)
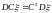 .
.
8)
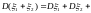
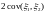 .
.
Если
,
то
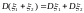 .
.
9)
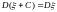 .
С – постоянная.
.
С – постоянная.
10)
 .
.
11)
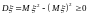
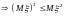 .
.
Двумерная
случайная величина
 называется распределенной
по нормальному закону,
если ее плотность распределения
называется распределенной
по нормальному закону,
если ее плотность распределения
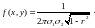
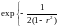
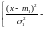

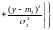 .
.
Здесь
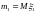 ,
,
,
,
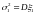 ,
,
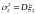 ,
,
 –
коэффициент
корреляции случайных величин
и
.
Для нормальной случайной величины
понятия независимости и некоррелируемости
эквивалентны.
–
коэффициент
корреляции случайных величин
и
.
Для нормальной случайной величины
понятия независимости и некоррелируемости
эквивалентны.
Двумерная случайная величина распределена равномерно в области , если ее плотность распределения
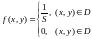
Здесь
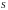 –
площадь области
.
–
площадь области
.
Пример
1. Дискретная
двумерная случайная величина
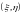 распределена по закону, приведенному
в таблице
распределена по закону, приведенному
в таблице
-

–1
0
2
–1
0,2
0,1
0,3
1
0,1
0,1
0,2
Определить:
1) Законы распределения составляющих и ;
2)
Условный закон распределения случайной
величины
при условии, что
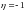 ;
;
3)
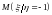 ;
;
4)
Коэффициент корреляции
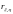 .
.
Решение. Имеем
|
–1 |
1 |
|
0,6 |
0,4 |
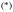
|
–1 |
0 |
2 |
|
0,3 |
0,2 |
0,5 |
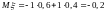 ,
, 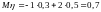 ,
,
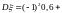
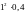 -
- ,
,
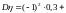
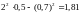 .
.
|
–1 |
1 |
|
2/3 |
|
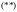
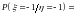
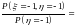
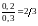 .
.
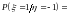
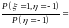
 .
.
Сравнивая
(*) и (**), видим, что
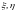 зависимые случайные величины:
зависимые случайные величины:
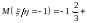
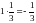 ;
;
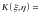

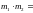


+
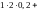
 =
=
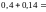
=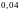 .
.
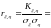
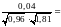
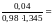
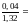
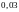 .
.
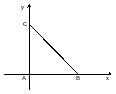
Пример 2.
Двумерная
случайная величина
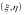 имеет равномерное распределение
вероятностей в треугольной области
АВС, то есть
имеет равномерное распределение
вероятностей в треугольной области
АВС, то есть
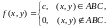
Найти
постоянную
 ,
одномерные плотности
,
одномерные плотности
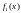 ,
,
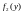 случайных величин
и
,
коэффициент корреляции
,
условную плотность
случайных величин
и
,
коэффициент корреляции
,
условную плотность
 и условное математическое ожидание
и условное математическое ожидание
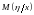 .
.
т.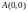 ,
т.
,
т.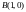 ,
т.
,
т.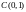 .
.
1)
Постоянную
 найдем из условия нормировки
найдем из условия нормировки

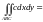
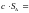
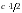 ,
,
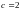 ,
,
где
–
площадь треугольника
 .
Обозначим область, ограниченную
треугольником
через
.
Тогда
.
Обозначим область, ограниченную
треугольником
через
.
Тогда

2)
Уравнение прямой
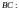
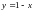 .
Тогда область
можно задать аналитически следующим
образом:
.
Тогда область
можно задать аналитически следующим
образом:
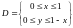 или
или
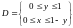 .
.
3)


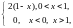
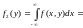
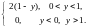
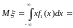
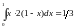 .
.
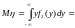
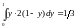 .
.
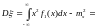
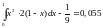 .
.
 .
.
4)
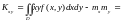
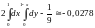 .
.

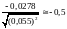 .
.
5)
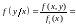

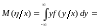
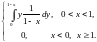
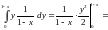
 .
.
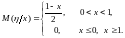
Пример
3. Случайная
точка
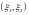 распределена равномерно внутри круга
радиуса
распределена равномерно внутри круга
радиуса

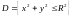 .
Найти математическое ожидание случайной
величины
.
Найти математическое ожидание случайной
величины
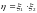 .
.
Решение. Плотность распределения вероятности
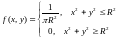
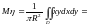
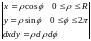 =
=
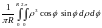 =
=

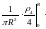
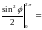
 .
.
Пример
4. Пара
случайных величин
и
имеет совместное нормальное распределение
с вектором математических ожиданий
 и ковариационной матрицей
и ковариационной матрицей

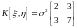 .
.
Известно,
что
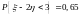 .
Найти
.
Найти

 .
.
Решение.
Совместная
нормальность пары случайных величин
и
обеспечивает нормальность каждой из
них и любой их линейной комбинации, в
частности величина
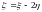 нормальна с параметрами
нормальна с параметрами

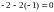 ,
,  .
.
Подставляя в последнее соотношение элементы ковариационной матрицы:
получим
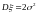 ,
,  ,
, 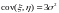 ,
,
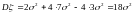 .
.
По
условию
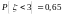 ,
откуда, используя нормальность
,
откуда, используя нормальность
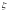 ,
,
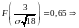
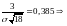
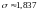 .
.
Искомые дисперсии равны, соответственно,
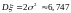 ,
, 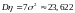 .
.
Пример
5. Случайный
вектор
 имеет вектор математических ожиданий
имеет вектор математических ожиданий
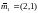 и корреляционную матрицу
и корреляционную матрицу
 .
.
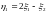 ,
,
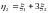 .
.
Вычислить
вектор математических ожиданий
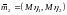 случайного вектора
случайного вектора
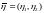 и корреляционную матрицу вектора
и корреляционную матрицу вектора
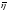 .
.
Решение.
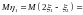
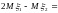
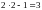 .
.
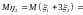
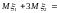
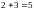 .
.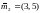 .
.
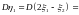
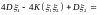
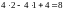 .
.
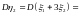
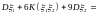
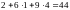 .
.
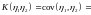
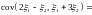
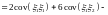
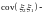
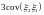 =
=
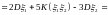
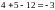 .
.
Ответ:
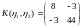 ,
.
,
.
Примеры для самостоятельного решения
1.
Дискретные случайные величины
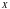 и
и
 независимы и имеют распределения:
независимы и имеют распределения:
У |
4 |
5 |
|
0,4 |
0,6 |
|
2 |
3 |
|
0,3 |
0,7 |
Найдите закон распределения случайной величины
 и
ее математическое ожидание.
и
ее математическое ожидание.
2.
Случайные величины
и
независимы и каждая имеет показательный
закон распределения с плотностью
распределения
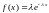 при
при
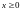 и
и
 при
при
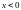 .
Найдите плотность вероятности суммы
этих величин.
.
Найдите плотность вероятности суммы
этих величин.
3.
Найдите математическое ожидание и
среднее квадратическое отклонение
случайной величины
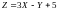 ,
если
,
если
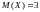 ,
,
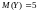 ,
,
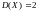 ,
,
 ,
а случайные величины
и
независимы.
,
а случайные величины
и
независимы.
4. Случайные величины и независимы и обе равномерно распределены на отрезке [0, 2]. Найдите функцию плотности вероятности случайной величины .
5.
Пусть
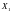 и
и
 - независимые одинаково распределенные
случайные величины, имеющие показательное
распределение с параметром
.
Найти распределение случайной величины
- независимые одинаково распределенные
случайные величины, имеющие показательное
распределение с параметром
.
Найти распределение случайной величины
 .
.
6.
Случайные величины
и
независимы
и каждая равномерно распределена на
(0, 1). Найдите плотность вероятности
случайной величины
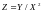 .
.
7.
Каждая из случайных величин
и
равномерно
распределена в интервале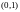 .
Полагая величины
и
независимыми,
найдите функцию распределения,
математическое ожидание и дисперсию
для каждой из величин
.
Полагая величины
и
независимыми,
найдите функцию распределения,
математическое ожидание и дисперсию
для каждой из величин
 и
и
 .
.
8. Закон распределения двумерной случайной величины задан таблицей
|
1 |
2 |
4 |
|
0,2 0,05 |
0,3 0,15 |
0,1 0,2 |
Найдите: а) безусловные законы распределения величин и ; б) закон распределения при условии, что .
9.
Равновозможны все положения случайной
точки
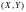 в треугольнике с вершинами
в треугольнике с вершинами
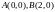 и
и .
Найти коэффициент корреляции случайных
величин
и
.
Найти линию регрессии
на
.
.
Найти коэффициент корреляции случайных
величин
и
.
Найти линию регрессии
на
.
10. В примере №8 найдите корреляции между и .
11.
По известной функции плотности вероятности
случайной величины
найдите функцию плотности вероятности
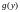 случайной величины.
случайной величины.
12.
Система случайных величин
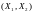 имеет функцию плотности вероятности
имеет функцию плотности вероятности
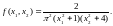 Найдите
плотность распределения
Найдите
плотность распределения
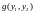 двумерной случайной величины
двумерной случайной величины
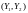 ,
если
,
если
 ,
,
 ,
,
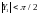 ,
,
 .
.
Ответы
|
6 |
7 |
8 |
|
|
0,12 |
0,46 |
0,42 |
,
|
2.
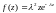 при
при
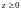 и
при
и
при
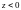 ;
;
3.
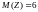 ,
,
 ;
;
4.
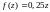 при
при
 ,
,
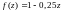 при
при
 ,
,
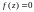 при остальных
при остальных
 ;
5.
;
5.
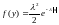 ;
;
6.
при
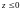 ,
,
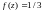 при
при
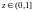 ,
,
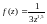 при
при
 ;
7.
;
7.
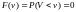 при
при
 ,
,
 при
при
 ,
,
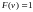 при
при
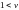 ,
,
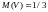 ,
,
 ,
,
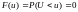 при
при
 ,
,
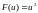 при
при
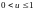 ,
,
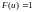 при
при
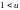 ,
,
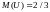 ,
,
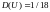 ;
;
8.
а |
|
1 |
2 |
4 |
, |
|
1 |
3 |
; б |
|
1 |
2 |
4 |
|
0,25 |
0,45 |
0,3 |
|
0,6 |
0,4 |
|
1/3 |
1/2 |
1/6 |
9.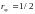 ,
,
 ;
10.
;
10.
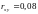 ;
;
11.
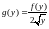 при
при
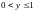 ,
,
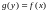 при
при
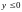 и
и
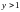 ;
;
12.
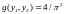 при
при
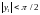 ,
,
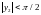 и
и
 при остальных
при остальных
 и
и
 .
.

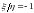

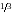

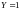


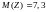 ;
;