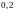Примеры непрерывных распределений

1) Равномерное распределение

2) Нормальное распределение (с параметрами )

, , .

Запись означает, что случайная величина распределена нормально с параметрами и .

3) Показательное распределение

.

4) Распределение Коши

.

5) Распределение Релея

_{6) Гамма-распределение с параметрами} ,

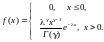
Здесь 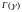– гамма-функция.

Математическим ожиданием случайной величины называется число

(1)

Говорят, что математическое ожидание у случайной величины существует, если ряд (интеграл) (1) сходится абсолютно.

Дисперсией случайной величины называется число

.

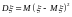Дисперсия вычисляется по формулам:

для дискретной случайной величины.

для непрерывной случайной величины, где .

Пример 1. Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытания равны 0,8 и независимы. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. Вывести формулу для ряда распределения числа испытаний.

Решение. Испытания заканчиваются на k-ом изделии, если первые (k-1) изделия пройдут испытания, а k – изделие не пройдет. Если случайное число испытаний, то

, .

ЗРВ будет иметь вид

X	1	2	3		k
p

Пример 2. В урне имеется четыре шара с номерами от 1 до 4. Извлекли два шара. Найти закон распределения и функцию распределения СВ X суммы номеров извлеченных шаров.

Решение. Ω={(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)}.

Закон распределения имеет вид

Х	3	4	5	6	7
P(X=xk)	1/6	1/6	2/6	1/6	1/6

Функция распределения

График F(x) имеет вид

Пример 3. Вероятность попадания стрелка при одном выстреле р=0,3. Найти закон распределения для СВ X - числа попаданий при 3 выстрелах.

Решение. Обозначим попадание через Y, непопадание - Н. Тогда

Ω={(НHН),(YHH),(HYH),(HHY),(YYH),(YHY),(HYY), (YYY)},

Х	0	1	2	3
Pn(Х=k)	q3=0,343	pq2=0,441	p2q=0,189	p3=0,227

Пример 4. Случайная величина Х распределена по закону, определяемому плотностью распределения вероятностей вида

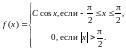
Найти константу С, вычислить

Решение. 1. Для нахождения С воспользуемся свойством нормировки . Или

2.

= .

3.

4.

Пример 5. Время безотказной работы некоторого узла сложного агрегата – экспоненциальная случайная величина со средним . Для увеличения надежности агрегата узел дублируется – ставят параллельно несколько одинаковых, но функционирующих независимо узлов. Сколько узлов следует запараллелить, чтобы с вероятностью, не меньшей чем 0,9, по крайней мере один из них не вышел из строя за 10 часов работы?

Решение.  – случайное время безотказной работы узла – имеет экспоненциальное распределение. Это означает, что

Известно, что математическое ожидание экспоненциальной случайной величины есть величина, обратная параметру: . Следовательно, вероятность отказа узла в течение 10 часов будет равна

.

Если запараллелено идентичных узлов, то событие {по крайней мере один из узлов не вышел из строя за 10 часов} является противоположным событию {все узлы вышли из строя за 10 часов}. Поэтому . Для последней вероятности (в силу независимости отказов запараллеленных узлов) получаем

.

Искомое количество может теперь быть найдено как наименьшее целое решение неравенства

.
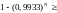