1.6. Метод Фурье решения задачи о колебаниях конечной струны с закрепленными концами

Рассмотрим другой метод решения задачи о колебаниях конечной струны. Пусть требуется найти решение дифференциального уравнения

удовлетворяющее начальным условиям:

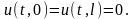
и граничным условиям:

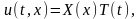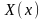Найдем сначала частные решения нашего уравнения , отличные от тождественного нуля, удовлетворяющие граничным условиям . Эти решения будем искать в виде где и 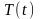отличны от тождественного нуля и 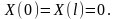Дифференцируя функцию дважды по переменным t и x и подставляя полученные производные в уравнение получим

или

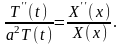
Левая часть этого уравнения не зависит от х, правая не зависит от t, поэтому правая и левая часть может быть только постоянной. Обозначая эту постоянную через 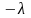, получим дифференциальные уравнения для определения функции и :

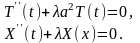
Решение уравнений отличны от тождественного нуля и

Ненулевые решения уравнения, удовлетворяющие граничному условию , называются собственными функциями, а те значения 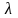,для которых эти решения существуют, называются собственными значениями краевой задачи . Легко показать, что если 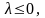то наше уравнение имеет единственное решение 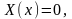удовлетворяющее граничному условию . Поэтому будем рассматривать случаи, когда

Общее решение уравнения 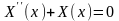имеет вид 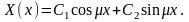Полагая в нем х=0 и х=l, получим систему уравнений для определения 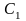и

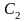
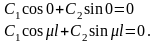
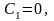
Отсюда следует, что 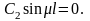Так как 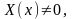то 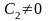, следовательно, , то есть 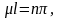где n=1,2…Таким образом, наше уравнение имеет ненулевые решения, удовлетворяющие граничному условию только при 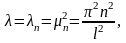и эти решения имеют вид

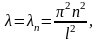Полагая получим уравнение 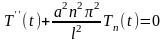для определения функций 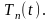Общее решение этих уравнений имеет вид

Таким образом, мы получили бесконечно много частных решений

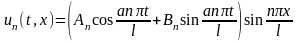
нашего уравнения, удовлетворяющих граничному условию .

Дифференциальное уравнение линейное однородное. Поэтому сумма конечного числа частных решений этого уравнения также является решением уравнения , удовлетворяющим граничному условию . Допустим, что решение исходной задачи можно искать в виде суммы бесконечного числа частных решений , то есть в виде ряда

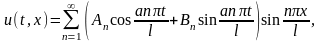
коэффициенты 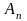и которого находятся таким образом, чтобы выполнялись начальные условия . Это возможно, если ряд можно дифференцировать дважды по переменным t и x. Дифференцируя ряд по переменной t, получим

Полагая здесь , получим 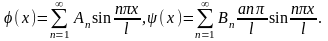Следовательно, числа и 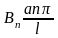являются коэффициентами Фурье в разложении функций и в ряд Фурье по синусам на отрезке [0,l], то есть

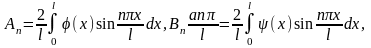
или

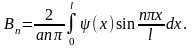
Таким образом, решение поставленной задачи имеет вид

,

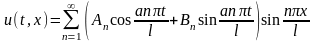где

Остается открытым вопрос, при выполнении каких условий ряд можно дифференцировать дважды переменным t и х. Приведем без доказательства ответ на этот вопрос.

Теорема. Если функция кусочно-непрерывную производную на отрезке [0,l] и удовлетворяет граничному условию 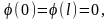то ряд можно дифференцировать почленно дважды по переменным t и х.

Физическая интерпретация решения

Колебания конечной струны с закрепленными концами получаются от наложения бесконечно большого числа колебаний, описываемых функциями :

каждое из которых называется собственным колебанием струны. Функции 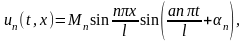можно представить в виде

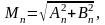
где Эта формула показывает, что собственное колебание любой точки х струны – это гармоническое колебание с амплитудой 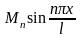и начальной фазой 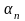. Притом все точки струны одновременно проходят состояние равновесия и одновременно достигают максимального отклонения от по­ложения равновесия. Такие колебания называются стоячими вол­нами. На рис. 1.13-1.15 показана форма струны в разные моменты вре­мени для n=1, n=2 и n=3.

Рис. 1.13. Рис. 1.14.

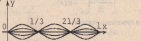
Рис. 1.15.

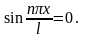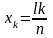Те точки струны, которые в процессе колебаний остаются неподвижными, называются узловыми точками, а те точки струны, которые имеют максимальную амплитуду колебаний, называются пучностями. Узловые точки определяются из уравнения Следовательно, узловыми точками n-й стоячей волны являются точки (k=0,1,2,…,n), пучностями точки - 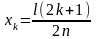(k=0,1,2,…,n-1).