1.14. Задача теплопроводности в бесконечном цилиндре
Пусть
в бесконечном цилиндре
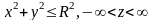
Задано
начальное распределение температур,
граничные точки цилиндра поддерживаются
при нулевой температуре. Требуется
найти температуру в любой точке цилиндра
в любой момент времени
.
Мы рассмотрим частный случай этой
задачи, когда начальное распределение
температур не зависит от переменной z
и не зависит от полярного угла
.
Это значит, что и решение этой задачи
не зависит от z
и
.
Следовательно, в цилиндрической системе
координат
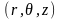задача
заключается в следующем.
Найти решение дифференциального уравнения
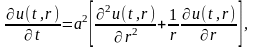
удовлетворяющее начальному условию
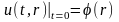
и граничным условиям
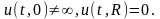
Сначала
найдем ненулевые решения нашего
уравнения, удовлетворяющие только
граничным условиям . Эти решения будем
искать в ви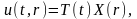де
где
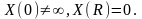
Дифференцируя функцию по t и по r дважды и подставляя результаты дифференцирования в наше уравнение, получим
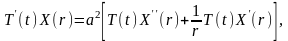
или
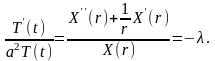
Отсюда следует, что
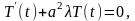
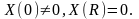
Как
известно
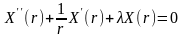уравнение имеет ненулевые решения,
удовлетворяющие граничным условиям
только при
где
-
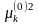положительные корни уравнения
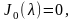и
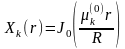
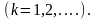этими решениями являются функции
При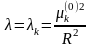
уравнение
принимает вид
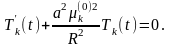
Общим решением этого уравнения являются функции
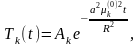где
-произвольные
постоянные.
Таким образом, ненулевыми решениями нашего уравнения , удовлетворяющими граничным условиям , являются функции
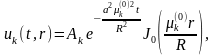где
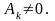Решение поставленной задачи будем
искать в виде ряда
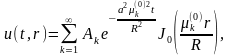
коэффициенты,
которого подбираются так, чтобы
выполнялось начальное условие . При
t=0,
получим
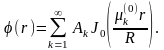
Отсюда следует, что
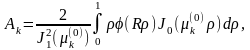
или
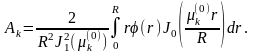
Таким образом, решение поставленной задачи находится по формуле (2.27), коэффициенты которой вычисляются по формуле (2.28).
Пример. Решить неоднородное уравнение параболического типа
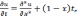0<x<1,
t>0.
При
начальных условиях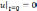 
и
однородных
краевых условиях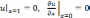 
Применяя метод Фурье разделения переменных, полагаем для решения соответствующего
однородного
уравнения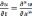 
при наших краевых условиях .
Приходим
к задаче Штурма-Лиувилля X’’(x)+λ2X(x)=0,
X’’(0)=0,
X(1)=0.
Находим собственные значения λk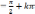
,
k=0,1,2,…и
соответствующие им собственные функции
Xk(x)=cos
λkx.
Решение задачи ищем в ви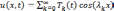де
,
где
.
Подставляя в основное уравнение, получим
Для
нахождения функции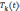 
разложим функцию 1-х в ряд Фурье по
косинусам на интервале (0,1):
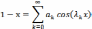
Так
как 
то получаем
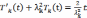при условии
.
Решая задачу Коши, находим ее решение
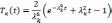
Подставляя
функцию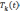 
в формулу для u(x,t),
находим искомое решение задачи :
,
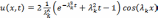где λk
В данной задаче рассматривается ограниченный стержень длины l=1 и решается уравнение теплопроводности стержня, где - температура стержня в точке х в момент времени t.
Задача для самостоятельного решения.
Дана
неограниченная пластина толщиной 2R при
температуре
.
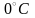Пластина нагревается с обеих сторон
одинаково постоянным тепловым потоком
q.
Найти распределение температуры по толщине пластины в любой момент времени t > 0.
Ответ:
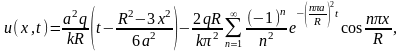
где k—коэффициент внутренней теплопроводности.
Указание. Задача приводится к интегрированию уравнения
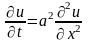при
условиях
