6.2 Простейшая задача вариационного исчисления. Уравнение Эйлера

Исследуем на экстремум функционал

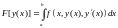, (6.1)

причем граничные точки допустимых кривых закреплены: y(a)=y₀ и y(b)=y₁. Будем полагать, что подынтегральная функция имеет непрерывные частные производные до 2-го порядка включительно по всем своим аргументам.

Пусть множество M образовано гладкими (т.е. y(x)c₁[a,b]) кривыми, проходящими через точки A и B (см. рис.). Простейшая задача вариационного исчисления состоит в отыскании на множестве M той кривой, на которой функционал (6.1) достигает экстремума.

М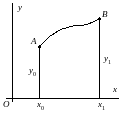 ожно показать, что необходимое условие экстрему­ма этого функционала приво­дит к уравнению

,

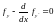называемому уравнением Эйлера. Таким образом, для того чтобы функционал достигал на некоторой функции y(x) экстремума, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера.

Уравнение Эйлера в общем случае является дифференциальным уравнением 2-го порядка. Его интегральные кривые y=y(x,C₁,C₂) называются экстремалями. Только на экстремалях может достигаться экстремум функционала (6.1).

Для нахождения кривой, реализующей экстремум функционала (1), следует проинтегрировать уравнение Эйлера и из условий на границе y(a)=y₀ и y(b)=y₁ определить обе произвольные постоянные С₁ и С₂, входящие в общее решение этого уравнения. Только на удовлетворяющих этим условиям экстремалях может реализоваться экстремум функционала. Однако для того чтобы установить, реализуется ли на них в действительности экстремум, и притом максимум или минимум, нужно воспользоваться достаточными условиями экстремума, которые приведены в специальной литературе.

Краевая задача

как известно, не всегда имеет решение, а если решение существует, то оно может быть не единственным. Заметим, что во многих вариационных задачах существование решения очевидно из физического или геометрического смысла задачи.

Пример 1. На каких кривых может достигать экстремума функционал

?

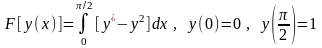Имеем

.

Составляем уравнение Эйлера : .

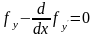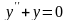Общее решение: y=С₁cosx+С₂sinx. Из граничных условий: y(0)=С₁1+С₂0=0, y(/2)=С₁0+С₂1=1С₁=0, С₂=1.

Следовательно, экстремум может достигаться лишь на кривой y=sinx.

Пример 2. .

Уравнение Эйлера: 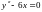 y(x)=x³+С₁x+С₂, y(0)=С₂=0; y(1)=1+С₁=1  С₁=0.

Ответ: y=x³.

Пример 3. .

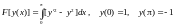Экстремали данной задачи определяются уравнением y(x)=С₁cosx+С₂sinx (см. пример 1). В граничных точках: y(0)=С₁=1, y()=–С₁=–1. Таким образом, граничные условия определяют лишь постоянную С₁, а константа С₂ может выбираться произвольно. Итак, искомая функция имеет вид y(x)=cosx+Сsinx (С – произвольная постоянная), т.е. задача имеет бесконечное множество решений.

6.3 О прямых методах вариационного исчисления

Дифференциальные уравнения (Эйлера) вариационных задач интегрируются в конечном виде лишь в исключительных случаях. В связи с этим естественно возникает потребность в иных методах решения этих задач. Основная идея так называемых прямых методов заключается в том, что вариационная задача рассматривается как предельная для некоторой задачи на экстремум функции конечного числа переменных. Эта задача на экстремум функции конечного числа переменных решается обычными методами математического анализа и алгебры.

Функционал F[у(х)] можно рассматривать как функцию бесконечного множества переменных. Это утверждение становится совершенно очевидным, если предположить, что допустимые функции могут быть разложены в степенные ряды

y(x) = a₀ + a₁ x + a₂ x² + ... + a_n xⁿ +...,

или в ряды Фурье

,

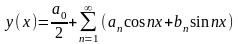или вообще в какие-нибудь ряды вида

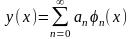, (6.2)

где (x) — заданные функции. Для задания функции у(x), представимой в виде ряда (6.2), достаточно задать значения всех коэффициентов {a_n }, и, следовательно, значение функционала F[y(x)] в этом случае определяется заданием бесконечной последовательности чисел a₀, a₁, a₂, ... , a_n, ..., т. е. функционал является функцией бесконечного множества переменных:

F[y(x)]= (a₀, a₁, ... , a_n, ...).

Следовательно, различие между вариационными задачами и задачами на экстремум функций конечного числа переменных состоит в том, что в вариационном случае приходится исследовать на экстремум функции бесконечного множества переменных.

Л. Эйлер для решения вариационных задач применял метод, называемый теперь конечно-разностным прямым методом. Пусть, к примеру, требуется найти решение простейшей задачи вариационного исчисления:

; , .

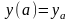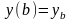Идея конечно-разностного метода заключается в том, что значения функционала F[y(x)] рассматриваются не на произвольных, допустимых в данной вариационной задаче, кривых, а лишь на ломаных, составленных из заданного числа п прямолинейных звеньев с заданными абсциссами вершин:

a+x, a+2x, ... , a+(n–1)x, где .

На таких ломаных функционал F[y(x)] превращается в функцию (y₁,y₂,...,y_n–1) ординат y₁,y₂,...,y_n–1 вершин ломаной, так как ломаная вполне определяется этими ординатами.

Итак, разбивая отрезок [a, b] на n равных частей точками

функционал F(y) можно приблизить на основе какой-либо квадратурной формулы, например прямоугольников, выражением

,

x=(b–a)/n, y_iy(a+ix),

так что задача оптимизации теперь имеет место для функции n–1 переменной y₁, … , y_n–1. Выбираем ординаты y₁, y₂,..., y_n–1 так, чтобы функция (y₁,y₂,...,y_n–1) достигала экстремума, т.е. определяем y₁, y₂,..., y_n–1 из системы уравнений

, , ..., .

В пределе при n→ с учетом некоторых ограничений, налагаемых на функцию f, получим точное решение вариационной задачи. Удобнее, однако, не совершать предельного перехода и значение функционала F(y) на указанных ломаных вычислять приближенно.

Пример 4. Найти экстремум функционала

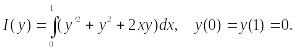
Решение. Отрезок [0, 1] разбивается на пять отрезков:

Тем самым получаем приближенную задачу на нахождение экстремума функционала

,

которая решается методами дифференциального исчисления:

;

;

;

.

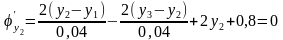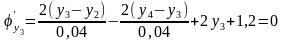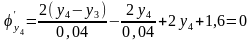В табл. 6.1 сравниваются y_i, полученные на основе данного приближения, с точными значениями y(0,2i) (округленными до четвертого знака).

Таблица 6.1

i	yi	y(0,2i)
1 2 3 4	–0,0286 –0,0503 –0,0580 –0,0442	–0,0287 –0,0505 –0,0583 –0,0444

Ниже приводится листинг программы для пакета Maple, с помощью которой легко выполнить указанные вычисления.

> restart;

> a:=0; b:=1; ya:=0; yb:=0; n:=5; # исходные данные

> h:=evalf((b-a)/n); # шаг x

> g:=diff(y(x),x)^2+y(x)^2+2*x*y(x); # подынтегральная функция в функционале

> s1:=subs(diff(y(x),x)=(y1-y0)/h,y(x)=y0,

x=a,g); # вычисление функции g в узловых точках x_i

> s2:=subs(diff(y(x),x)=(y2-y1)/h,y(x)=y1,x=a+h,g);

> s3:=subs(diff(y(x),x)=(y3-y2)/h,y(x)=y2,x=a+2*h,g);

> s4:=subs(diff(y(x),x)=(y4-y3)/h,y(x)=y3,x=a+3*h,g);

> s5:=subs(diff(y(x),x)=(y5-y4)/h,y(x)=y4,x=a+4*h,g);

> F:=s1+s2+s3+s4+s5; # функционал

> eqns:={diff(F,y1)=0,diff(F,y2)=0,diff(F,y3)=0,

diff(F,y4)=0, y0=ya,y5=yb}; # система уравнений

> rez:=solve(eqns,{y0,y1,y2,y3,y4,y5}); # решение

rez := {y3 = –.05808400444, y2 = –.05033254335, y4 = –.04415882571, y1 = –.02859438400, y0 = 0, y5 = 0}

Метод Эйлера не имеет никаких преимуществ перед другим прямым методом – методом Ритца, а часто даже уступает ему из-за более низкой точности и слишком большого числа неизвестных параметров и поэтому на практике используется редко.

Идея метода Ритца заключается в том, что значения некоторого функционала F[y(x)] рассматриваются не на произвольных допустимых кривых данной вариационной задачи, а лишь на всевозможных линейных комбинациях вида 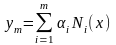с постоянными коэффициентами, составленных из m первых функций некоторой выбранной последовательности функций, называемых координатными или базисными,

N₁(x), N₂(x), ..., N_m(x), ....

Функции должны быть допустимыми в рассматриваемой задаче, что налагает некоторые ограничения на выбор последовательности функций N_i(x). На таких линейных комбинациях функционал F[y(x)] превращается в функцию (₁, ₂, ..., _m) коэффициентов ₁, ₂, ..., _m . Эти коэффициенты выбираются так, чтобы функция (₁, ₂, ..., _m) достигала экстремума; следовательно, ₁, ₂, ..., _m должны быть определены из системы уравнений

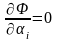, i = 1, 2,…, m.

Совершая предельный переход при m, получим в случае существования предела функцию 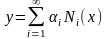, являющуюся точным решением рассматриваемой вариационной задачи. Если не совершать предельного перехода, а ограничиться лишь m первыми членами, то получим приближенное решение вариационной задачи.

Если таким методом определяется абсолютный минимум функционала, то приближенное значение минимума функционала находится с избытком. При нахождении тем же методом максимального значения функционала получим приближенное значение максимума функционала с недостатком.

Выбор последовательности функций N₁, N₂..., N_m сильно влияет на степень сложности дальнейших вычислений, и поэтому от удачного выбора базисной системы функций в значительной мере зависит успех применения этого метода.

Для того чтобы функции были допустимыми, прежде всего, необходимо удовлетворить граничным условиям (конечно, не следует забывать и о других ограничениях, которые могут быть наложены на допустимые функции, например, требованиях, касающихся их непрерывности или гладкости, а также полноты).

Рассмотрим подходы к решению простейшей задачи вариационного исчисления методом Ритца. В этой задаче граничные условия 1-го рода y(a)=y₀, y(b)=y₁ обычно играют роль главных условий. Поэтому множество допустимых функций, на которых ищется экстремум, приходится ограничивать только теми функциями, которые априори удовлетворяют этим условиям. Применительно к методу Ритца это означает выбор такой аппроксимации , которая заведомо удовлетворяет указанным условиям вне зависимости от того, какие значения принимают параметры {_i}.

Если граничные условия однородны, т.е. y(a)=y(b)=0, то проще всего в качестве базисных функций выбрать функции, удовлетворяющие этим граничным условиям: N_i(a)=N_i(b)=0, i=1, 2, ..., m. Например,

,

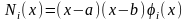где _i(x) – какие-нибудь непрерывные функции, или

(k=1, 2, ...).

Очевидно, что при этом и аппроксимация при любых _i будет удовлетворять тем же однородным граничным условиям.

Если условия неоднородны, т.е. у(a)=y₀, у(b)=y₁, где хотя бы одно из чисел y₀ или y₁ отлично от нуля, то решение вариационной задачи можно искать в виде

, (6.3)

где (x) удовлетворяет заданным граничным условиям: (a)=y₀, (b)=y₁ , а функции N_i(x) удовлетворяют соответствующим однородным граничным условиям, т.е. в рассматриваемом случае N_i(a)=N_i(b)=0. Очевидно, что при таком выборе при любых _i функции y_m(x) удовлетворяют заданным граничным условиям. В качестве функций (x) можно выбрать, например, линейную функцию

^{. (6.4)}

Пример 5. Найти экстремаль функционала

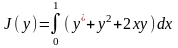; y(0)=4, y(1)=5.

Решение. Здесь граничные условия неоднородные, поэтому в аппроксимации (3) функция (x) отлична от нуля и удовлетворяет этим условиям. В качестве (x) согласно (4) возьмём (x)=x+4 (проверьте для a=0, b=1, y₀=4, y₁=5). В качестве базисных функций выбираем N_k(x)=x^k+1–x^k, k=1, 2, 3, ... . Эти функции удовлетворяют однородным граничным условиям N_k(0)=N_k(1)=0. Для m=2 имеем

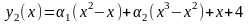
и

.

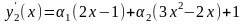После подстановки и 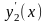в функционал J и интегрирования получим

.

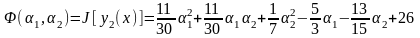Воспользовавшись необходимыми условиями экстремума функции 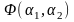, находим

,

.

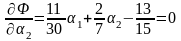Решив систему, получим 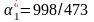, . Следовательно, приближенное выражение 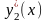для экстремали y(x) имеет вид

.

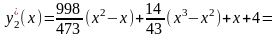
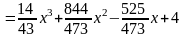В данном случае существует точное решение поставленной задачи. Действительно, составляя уравнение Эйлера, получим , которое является линейным неоднородным дифференциальным уравнением с постоянными коэффициентами. Его общее решение 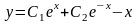. С учетом краевых условий y(0)=4, y(1)=5, находим

.

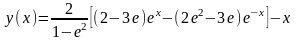Сравним полученное методом Ритца приближенное решение и точное при некоторых значениях аргумента (табл. 6.2).

Таблица 6.2

x	0,0	0,2	0,4	0,6	0,8	1,0
y(x)	4,000	3,85074	3,86405	4,04850	4,41951	5,000
	4,000	3,85199	3,86235	4,04673	4,42073	5,000
	0,000	3,85075	3,86409	4,04847	4,41949	0,000

Сравнение показывает, что точное и приближенное решение совпадают с точностью до 0,002. Это число может служить характеристикой погрешности аппроксимации.

Представленные шаги решения данной задачи могут быть реализованы в пакете компьютерной математики Maple с помощью команд:

> restart;

> z:=x->((a1+a2*x)*x*(x-1)+x+4); # аппроксимация решения

> F:=int((diff(z(x),x))^2+z(x)^2+2*x*z(x),

x=0..1); # функционал

> eqns:={diff(F,a1)=0,diff(F,a2)=0}; # система уравнений

> r:=solve(eqns,{a1,a2}); evalf("); # решение системы

> phi:=x->subs(r,z(x)): phi(x); collect(phi(x),x);

> t:=dsolve({diff(diff(y(x),x),x)-y(x)=x,

y(0)=4,y(1)=5},y(x)); # получение точного решения

> for t from 0 by 0.2 to 1 do printf(`x=%3.1g z=%7.5g u=%7.5g\n`,t,phi(t),u(t)); od; # табулирование найденного приближенного и точного решений

Если в сумме взять три слагаемых, то получим трехэлементную аппроксимацию . Путем аналогичного применения процедуры Ритца получим

.

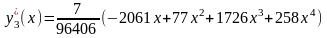В приведенном тексте Maple-программы для этого нужно поменять соответствующие строки:

> z:=x->((a1+a2*x+a3*x^2)*x*(x-1)+x+4);

> eqns:={diff(F,a1)=0,diff(F,a2)=0,diff(F,a3)=0};

> r:=solve(eqns,{a1,a2,a3});

Из табл. 6.2 видно, что данное приближенное решение отличается от точного решения уже не более чем на 410^–5. Таким образом, трехэлементная аппроксимация дает на два порядка лучший результат, чем двухэлементная аппроксимация. Если с увеличением числа параметров (элементов) аппроксимации ₁, ₂, ..., _m приближенное решение 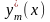стремится к точному решению y(x), то говорят, что имеется сходимость аппроксимации. Скорость сходимости является характеристикой процесса сходимости, позволяющей судить о том, как быстро приближается к y(x) c увеличением m.

В рассмотренном примере сходимость, очевидно, имеет место, а скорость сходимости достаточно высокая: добавление одного элемента аппроксимации привело к добавлению как минимум одной верной значащей цифры. Еще можно сказать о хороших аппроксимирующих свойствах функций N_i(x)=xⁱ⁺¹–xⁱ, i=1,2,..., поскольку всего первые три такие функции обеспечивают четыре верных знака в значениях искомой функции.

Всем приведенным характеристикам можно дать строгие определения, используя различные метрики конечномерных функциональных пространств. Подробное изложение этого вопроса, выходит за рамки данных методических указаний.

Для иллюстрации факта, что в методе Ритца минимальное значение функционала определяется с избытком, вычислим три числа:

;

;

.

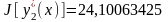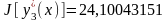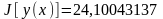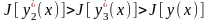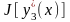Видно, что , т.е. приближенные значения функционала стремятся к точному значению сверху. Отметим характерную для прямых методов особенность: с увеличением числа элементов аппроксимации ошибка вычисления функционала уменьшается быстрее, чем ошибка вычисления функции . В рассматриваемом случае при переходе от к имеем у функционала три новых верных значащих цифры, в то время как значения самой функции стали точнее лишь на одну-две цифры.