7. Функция комплексного переменного

Извлечение корня

Корень n-ой степени из комплексного числа z имеет n различных значений, которые находятся по формуле

Элементарные функции комплексного переменного

Значения показательной функции комплексного

переменного вычисляются по формуле

Показательная функция обладает следующими

свойствами: где и - любые комплексные числа; т.е. является периодической функцией с основным периодом .

Тригонометрические функции sinz и cosz выражаются через показательную:

Функции и - периодические с

Действительным периодом и имеют только действительные нули и соответственно.

Функции tgz и ctgz определяются равенствами

Для тригонометрических функций комплексного переменного остаются в силе все известные формулы тригонометрии.

Гиперболические функции shz, chz, thz, cthz определяются

равенствами

Имеют место тождества shz=-isiniz, chz=cosiz.

Логарифмическая функция Lnz, где , определяется как функция, обратная показательной, причем

Значение функции, которое получается при k=0, называется

главным значением и обозначается

логарифмическая функция обладает следующими свойствами:

Функции Arcsinz, Arccosz, Arctgz, Arcctgz определяются

как обратные к функциям sinz, cosz, tgz, ctgz соответственно.

Так, если , то ω называется арккосинусом числа z и обозначается ω=Arccosz. Все эти функции являются

многозначными и выражаются через логарифмическую:

Значения, соответствующие главному значению

логарифма, обозначаются теми же символами со строчной буквы (arcsinz, arccosz, arctgz, arcctgz); они называются главными

значениями. Общая степенная функция , где α—любое

комплексное числе, определяется соотношением Эта функция многозначная; значение называется главным значением. Общая показательная функция , определяется равенством . Главное значение этой функции .

Кривые на комплексной плоскости

Уравнение вида z=z(t)= х(t)+iy(t) определяет на комплексной плоскости кривую, параметрические уравнения которой имеют вид Исключением параметра t из этих уравнений получаем уравнение кривой в виде F (x,у)=0.

Дифференцирование функций комплексного

переменного, условия Коши — Рнмана

Пусть функция определена в некоторой

области G комплексного переменного z. Пусть точки z и z+Δz

принадлежат области G. Введем обозначения

Функция , называется дифференцируемой о

точке , если отношение имеет конечный предел

при . Этот предел называется производной функции

и обозначается , .

Пусть , тогда в каждой точке дифференцируемости функции f(z) выполняются соотношения

называемые условиями Коши — Римана. Обратно, если в некоторой точке (x, у) выполняются условия Коши — Римана и, кроме того, функции и = и(х, у) и υ = υ (х, у) дифференцируемы как функции двух действительных переменных, то функция является дифферен­цируемой в точке z=x+iy как функция комплексного переменного z.

Функция называется аналитической в данной точке z, если она дифференцируема как в самой точке z, так и в некоторой ее окрестности. Функция называется аналитической в области G, если она аналитична в каждой точке .Производная аналитической функции вычисляется по формулам

Пользуясь условиями Коши—Римана, можно восстановить

аналитическую функцию , если известна ее

действительная часть или мнимая часть

и, кроме того, задано значение функции в некоторой точке . Пусть, например, Определить аналитическую функцию f(z). В силу условий имеем

Интегрируя уравнение по переменной x, находим мнимую часть

Слагаемое С(у) представляет собой постоянную (относительно х) интегрирования. Дифференцируя по у, получаем , откуда С (у)С. Таким образом, имеем

Из условия f(0) ==1, откуда С=0; итак,

Интегрирование функций комплексного переменного

Пусть однозначная функция определена и непрерывна в области G, а Г — кусочно-гладкая кривая, лежащая в G;

-действительные функции переменных х и у. Вычисление

интеграла от функции комплексного переменного

z сводится к вычислению криволинейных интегралов по

координатам:

Если кривая Г задана параметрическими уравнениями x=x(t), y= y(t), а начальная и конечная точки дуги соответствуют значениям t = α и t=β, то

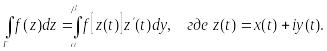
Если — аналитическая функция в односвязной области G, то интеграл не зависит от пути интегрирования (зависит только от начальной и конечной точек). В этом

случае для вычисления интеграла применяется формула

Ньютона — Лейбница

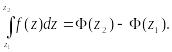
где Ф (z) —какая-либо первообразная для функции f(z), т. е, в области G, Если функция является аналитической в области G, ограниченной кусочно-гладким замкнутым контуром Г, и на самом контуре, то

(Теорема Коши) и для любой внутренней точки (интегральная формула Коши)

Ряд Лорана

Функция , однозначная н аналитическая в кольце разлагается в этом кольце в ряд Лорана

коэффициенты находятся по формулам

Здесь Г—произвольная окружность с центром в точке , лежащая внутри заданного кольца. Разложение в ряд Лорана единственно. В формуле ряды

называются соответственно гласной частью ряда Лорана и

правильной частью ряда Лорана. На практике для нахождения коэффициентов , если это возможно, используют готовые разложения элементарных функций в ряд Тейлора.

Изолированные особые точки однозначной

аналитической функции

Точка называется изолированной особой точкой функции , если f (z)- однозначная и аналитическая функция в круговом кольце кроме самой точки . Функцию в окрестности точки можно разложить в ряд Лорана(6), сходящийся в кольце .

При этом возможны три различных случая, когда ряд Лорана:

1. не содержит членов с отрицательными степенями

разности В этом случае называется устранимой особой точкой функции ;

2) содержит конечное число членов с отрицательными степенями разности .

В этом случае называется полюсом порядка n функции ; 3) содержит бесконечное число членов с отрицательными степенями разности

.

В этом случае называется существенно особой точкой функции . При определении характера изолированной особой точки используются следующие утверждения.

1. Для того чтобы точка являлась устранимой особой

точкой аналитической функции , необходимо и достаточно существование предела

Для того чтобы точка являлась полюсом аналитической

функции , необходимо и достаточно существование

предела

2. Для того чтобы точка являлась полюсом порядка п аналитической функции f(z), необходимо и достаточно, чтобы функцию f(z) можно было представить в виде —функция аналитическая в точке , причем . .Пусть —изолированная особая точка функции —функции аналитические в точке . Если числитель и все производные до к—1 порядка включительно в точке равны нулю, знаменатель и все производные до l-1 порядка включительно также равны нулю в точке , то при l>k точка является полюсом порядка n=l—k аналитической функции f(z). (Если то точка является устранимой особой точкой аналитической функции f(z).) В частном случае, при k=0, l = 1 имеем: если — полюс первого порядка функции f(z).

3. Пусть при аналитическая функция не имеет пределов ни конечного, ни бесконечного. Это условие является необходимым и достаточным для того, чтобы точка была существенно особой точкой функции .

Вычеты

Пусть — изолированная особая точка функции . Вычетом функции f (z) в точке называется число, обозначаемое символом и определяемое равенством

Замкнутый контур интегрирования γ лежит в области аналитичности функции f (z) и не содержит внутри других особых точек функции f (z), кроме . В лорановском разложении f (z) в окрестности точки : . Вычет в устранимой особой точке равен нулю. Вычет функции f (z) в полюсе n-гo порядка вычисляется по формуле

при n=1

Если функция в окрестности точки представляется как частное двух аналитических функций, причем (в этом случае — полюс первого порядка функции f (z)), то

Если точка есть существенно особая точка функции

, то вычет вычисляется по формуле.

Основная теорема Коши о вычетах.

Если функция является аналитической на границе Г области G и всюду внутри области, за исключением конечного числа особых точек то

Вычисление несобственных интегралов от

рациональных функций

Пусть R (x) — рациональная функция, где и - многочлены степеней

k и l соответственно. Если R (х) непрерывна на всей действительной оси и , т.е. степень знаменателя, по крайней мере, на две единицы больше степени числителя, то

здесь сумма вычетов функции берется по всем полюсам , расположенным в верхней полуплоскости Im z>0.

Вычисление несобственных интегралов

специального вида

Пусть R (x) — рациональная функция, где и - многочлены степеней k и l соответственно. Если R (х) непрерывна на всей действительной оси и (т. е. R(x) – правильная рациональная дробь), то

где сумма вычетов функции берется по всем полюсам , расположенным в верхней полуплоскости Im z>0.

Вычисление определенных интегралов

специального вида

Пусть R —рациональная функция cos t и sin t, непрерывная внутри промежутка интегрирования. Полагаем , тогда

Имеем

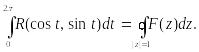
где путь интегрирования—окружность единичного радиуса с

центром в начале координат. Контурный интеграл в правой

части равенства с помощью вычетов функции F(z) берется по всем особым точкам, лежащим в области | z|< 1.