
- •Часть 3
- •(Кафедра «высшей математики и физико-математического моделирования») методические указания
- •Часть 3
- •Введение
- •1. Числовые ряды
- •2. Функциональные ряды
- •1. Двойной интеграл
- •4. Тройные интегралы
- •5. Криволинейные интегралы
- •4. Поверхностные интегралы
- •Применения поверхностных интегралов механике
- •Поверхностные интегралы второго рода
- •7. Функция комплексного переменного
- •2. Преобразование Лапласа
- •Заключение
- •Библиографический список
- •1. Числовые ряды……….……………………………………1
- •Часть 3
- •Федотенко Галина Федоровна в авторской редакции
2. Функциональные ряды
Основные теоретические сведения
Ряд
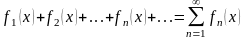 ,
(8)
,
(8)
члены которого – функции от х, называется функциональным.
Множество значений аргумента х, при которых функции
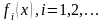 определены
и функциональный ряд (8) сходится,
определены
и функциональный ряд (8) сходится,
называется
областью
сходимости
этого ряда. При действительном значении
аргумента областью сходимости является
какой-либо промежуток оси ОХ. При
конкретном значении
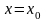 ряд (1) становится числовым. Функция
ряд (1) становится числовым. Функция
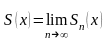 ,
где
,
где
 - сумма первых n
членов ряда (8), а х принадлежит области
сходимости, называется суммой ряда.
Разность между суммой S(x)
сходящегося ряда и его частичной суммой
- сумма первых n
членов ряда (8), а х принадлежит области
сходимости, называется суммой ряда.
Разность между суммой S(x)
сходящегося ряда и его частичной суммой
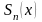 называется остатком ряда (8):
называется остатком ряда (8):
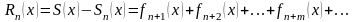 ,
,
причем
в области сходимости ряда
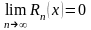 .
.
Сходящийся функциональный ряд (8) называется
равномерно сходящимся в некоторой области Х, если для
любого
сколь угодно малого числа ε >0 найдется
такое целое число N
>0, начиная с которого, т.е. при n
N,
выполняется неравенство
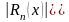 одновременно сразу для всех х из области
Х. Достаточным
признаком равномерной сходимости рядов
является следующий признак Вейерштрасса.
одновременно сразу для всех х из области
Х. Достаточным
признаком равномерной сходимости рядов
является следующий признак Вейерштрасса.
Ряд
(8) равномерно
сходится в данной области Х,
если существует такой сходящийся
числовой ряд
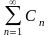 ,
что для всех значений х
,
что для всех значений х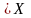 имеет место неравенство
имеет место неравенство
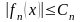 .
.
При
этом сходящийся числовой ряд
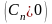 называется
называется
мажорантой для ряда (8).
Пример.
Ряды
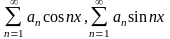 являются равномерно сходящимися в
любой области, если ряд
абсолютно сходится, т.к.
являются равномерно сходящимися в
любой области, если ряд
абсолютно сходится, т.к.
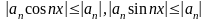 ,
а ряд
,
а ряд
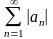 сходится.
сходится.
Свойства равномерно сходящихся рядов:
1. Если члены равномерно сходящегося ряда (8) непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке.
2. Равномерно сходящийся ряд (8) можно почленно интегрировать в данной области Х, если его члены непрерывны в области Х, причем сумма интегралов от членов ряда равна интегралу от суммы данного ряда:
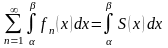 ,
где
,
где
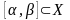
3.
Если ряд (8) сходится к сумме S(x)
на отрезке Х, причем его члены имеют
непрерывные производные
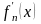 при х
и ряд, составленный из производных
при х
и ряд, составленный из производных
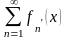 ,
равномерно сходящийся на том же отрезке,
то
,
равномерно сходящийся на том же отрезке,
то
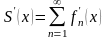 ,
т.е. ряд (8) можно почленно дифференцировать.
,
т.е. ряд (8) можно почленно дифференцировать.
Эти свойства функциональных рядов будут в дальнейшем использованы в заданиях 17-18 при нахождении суммы ряда (см. пункт 2.4).
Нахождение области сходимости
функциональных рядов
Для определения области сходимости функционального
ряда (8) достаточно применить к этому ряду известные признаки сходимости, считая аргумент х фиксированным.
Например, при использовании признаков Даламбера или Коши поступают так:
Находят q(x) по одной из формул (если пределы
существуют)
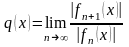 или
или
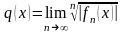 (9)
(9)
Решают неравенство q(x)<1 (т.к. по признакам
Даламбера и Коши ряд сходится при q<1 и расходится при q>1). В результате находим интервал сходимости.
Исследуется поведение ряда в концевых точках
интервала сходимости.
Пример. Найти область сходимости ряда
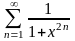
Решение. Рассмотрим три случая
Если
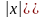 , то
, то
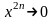 при
и
при
и
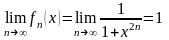 .
Необходимый признак сходимости ряда
не выполнен. Следовательно, ряд расходится
при -1<x<1.
.
Необходимый признак сходимости ряда
не выполнен. Следовательно, ряд расходится
при -1<x<1.
Если
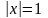 , то также получаем расходящийся ряд
, то также получаем расходящийся ряд
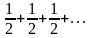
Если
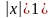 ,
то применим первый признак сравнения
,
то применим первый признак сравнения
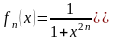 ,
где сходящийся ряд
,
где сходящийся ряд
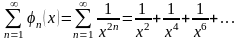 представляет
представляет
собой сумму бесконечно убывающей геометрической
прогрессии
со знаменателем
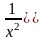 ,
т.е.
.
Итак, исследуемый ряд сходится при
;
его область сходимости
,
т.е.
.
Итак, исследуемый ряд сходится при
;
его область сходимости
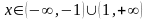
Нахождение суммы функционального ряда
Рассмотрим некоторые приемы нахождения суммы
функционального ряда и области его сходимости к этой сумме.
Нахождение суммы ряда почленным интегрированием.
Пусть дан ряд вида
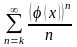 .
По признаку Коши или
.
По признаку Коши или
признаку
Даламбера область
сходимости определяется
неравенством
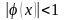 .
Если
.
Если
 ,
то ряд
,
то ряд
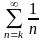 - расходящийся.
- расходящийся.
Если
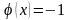 ,
то ряд
,
то ряд
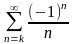 сходится условно (по признаку Лейбница).
Следовательно, область сходимости
находится из неравенства
сходится условно (по признаку Лейбница).
Следовательно, область сходимости
находится из неравенства
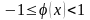 .
Затем делаем
замену
.
Затем делаем
замену
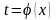 в исходном ряде; получаем степенной ряд
в исходном ряде; получаем степенной ряд
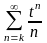 с областью сходимости
с областью сходимости
![]() .
Используем формулу для вычисления суммы
членов бесконечно убывающей геометрической
прогрессии со знаменателем
.
Используем формулу для вычисления суммы
членов бесконечно убывающей геометрической
прогрессии со знаменателем
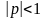
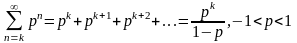
и
очевидное равенство
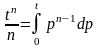
Учитывая,
что степенной ряд можно почленно
интегрировать по любому отрезку
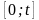 ,
целиком принадлежащему интервалу
сходимости, и используя формулу (13),
получаем
,
целиком принадлежащему интервалу
сходимости, и используя формулу (13),
получаем
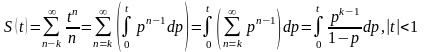 Заметим,
что так как ряд (12) сходится в граничной
точке t=-1,
то сумма ряда непрерывна в этой точке
(справа) и
Заметим,
что так как ряд (12) сходится в граничной
точке t=-1,
то сумма ряда непрерывна в этой точке
(справа) и
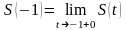 .
Далее вычисляем интеграл (с переменным
верхним пределом), заменяем t
на
.
Далее вычисляем интеграл (с переменным
верхним пределом), заменяем t
на
 и получаем ответ.
и получаем ответ.
Если дан ряд вида
 ,
то следует либо
,
то следует либо
применить
теорему о почленном интегрировании
степенного ряда дважды, либо разложить
дробь на элементарные
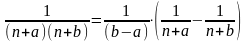 и
вычислить сумму каждого ряда почленным
интегрированием.
и
вычислить сумму каждого ряда почленным
интегрированием.
Пример.
Найти сумму ряда
 и указать область
и указать область
его сходимости к этой сумме.
Решение. Данный ряд степенной. Находим его интервал сходимости. По признаку Коши имеем
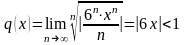 .
Из неравенства находим
.
Из неравенства находим
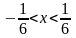 .
Исследуем поведение ряда в граничных
точках. При
.
Исследуем поведение ряда в граничных
точках. При
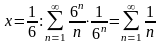 -
расходящийся гармонический ряд. При
-
расходящийся гармонический ряд. При
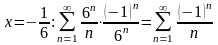 - условно сходящийся ряд по признаку
Лейбница. Следовательно, данный ряд
сходится при
- условно сходящийся ряд по признаку
Лейбница. Следовательно, данный ряд
сходится при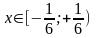 .
Для нахождения суммы ряда сделаем замену
.
Для нахождения суммы ряда сделаем замену
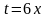 .
Получим геометрический ряд
.
Получим геометрический ряд
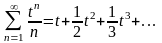 ,
сходящийся при
,
сходящийся при
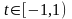 .
Используя почленное интегрирование
степенного ряда, получаем:
.
Используя почленное интегрирование
степенного ряда, получаем:
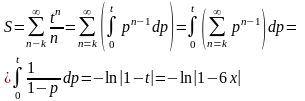
Разложение функций в степенной ряд Тейлора
Всякая
функция f(x),
бесконечно дифференцируемая в интервале
 ,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд Тейлора
,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд Тейлора
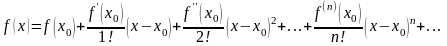 ,
,
если
в этом интервале выполняется условие:
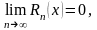 где
где
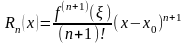 остаточный
член формулы Тейлора, записанный в форме
Лагранжа,
остаточный
член формулы Тейлора, записанный в форме
Лагранжа,
 где
где
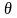 -
положительное число меньше 1.
-
положительное число меньше 1.
При
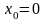 ряд
Тейлора называют рядом Маклорена:
ряд
Тейлора называют рядом Маклорена:
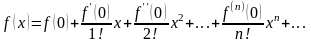 .
.
5)
Если в некотором интервале, содержащем
точку
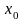 ,
все производные
,
все производные
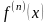 ограничены некоторой константой, т.е.
при любом n
выполняется неравенство
ограничены некоторой константой, т.е.
при любом n
выполняется неравенство
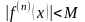 ,
где М – положительная постоянная, то
.
Тогда функция f(x)
будет суммой ряда , причем только для
тех значений х, при которых
,
где М – положительная постоянная, то
.
Тогда функция f(x)
будет суммой ряда , причем только для
тех значений х, при которых
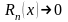 при
(необходимое
и достаточное условие равенства в
разложении f(x)
в ряд Тейлора).
при
(необходимое
и достаточное условие равенства в
разложении f(x)
в ряд Тейлора).
Приведем основные разложения в ряд Маклорена:
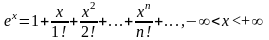
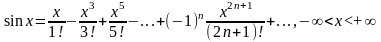
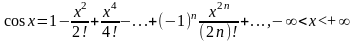
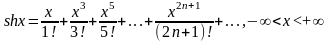
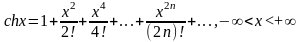
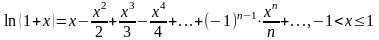
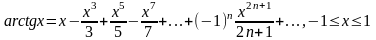
Биномиальный ряд
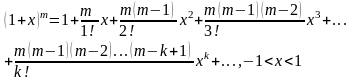
Причем
это последнее разложение при
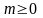 является
является
абсолютно сходящимся рядом в граничных точках интервала,
т.е.
при х=-1
и при х=1;
при
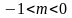 ряд расходится при
ряд расходится при
х=-1
и условно сходится при при х=1;
при
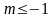 ряд расходится на обеих границах
интервала (-1;1).
ряд расходится на обеих границах
интервала (-1;1).
При разложении функции f(x) в ряд Тейлора по степеням х (когда ) преобразуют, если возможно, функцию f(x) к виду, допускающему использование основных разложений , а также сложение (вычитание) рядов, умножение ряда на число. Затем определяют область сходимости полученного ряда к функции f(x).
Пример. Разложить ln x в ряд по степеням (х-1).
Решение.
Имеем
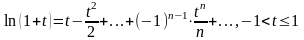 ,
то
,
то
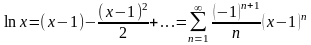 (t=x-1),
где
(t=x-1),
где
область
сходимости есть полуинтервал
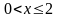 .
.
