4. Работа силы, мощность, коэффициент полезного действия

Работа A силы при прямолинейном движении материальной точки и поступательном движении абсолютно твердого тела определяется соотношением

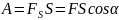, (3.4.1)

г де S – перемещение тела под действием силы F, α – угол между направлением силы и направлением перемещения, F_S – проекция вектора сила на направление перемещения (рис. 3.4.1).

Искомая работа A на графике зависимости F_S от S равна площади фигуры под кривой (см. рис. 3.4.2).

В зависимости от взаимной ориентации векторов силы и перемещения работа может быть величиной положительной, отрицательной или равной нулю. Из (3.4.1) следует, что если:

• α<π/2, А>0,

• α>π/2, А<0,

• α=π/2, А=0.

З адача 3.2. По строительной площадке равномерно перемещают стальную балку на расстояние S = 500 м, действуя на нее с силой F = 5000 Н, направленной под углом φ = 60⁰ к горизонту. Каковы работы сил, действующих на балку во время движения?

Решение. Силы, действующие на балку, показаны на рис. 1. Для определения работ этих сил, согласно (3.4.1), необходимо знать модули сил и углы между каждой силой и направлением движения. Из рис. 1 следует:

угол между и 60⁰,

угол между и 90⁰,

угол между 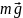и 90⁰,

угол между 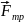и 180⁰.

Чтобы найти модуль силы трения, запишем второй закон Ньютона в векторном виде. Так как по условию задачи движение равномерное ( =0), векторная сумма сил равна нулю.

.

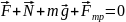Проекция этого уравнения на ось OX, направленную горизонтально вправо:

.

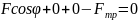Таким образом,

.

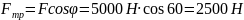Рассчитаем работы сил:

A_F=FScos60=5000·500·1/2=1250000 Дж=1,25 МДж,

A_N=NScos0=0Дж,

A_mg=mgScos0=0Дж,

A_Fтр=F_трScos180=2500·500·(1)=1250000 Дж=1,25 МДж.

Ответ: A_F=1,25 МДж; A_N=0Дж; A_mg=0Дж; A_Fтр=1,25 МДж.

Мощность P – характеризует скорость совершения работы:

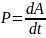. (3.4.2)

Если учесть, что 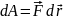, получим

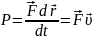. (3.4.3)

То есть мощность равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы. Единица измерения: [P]= [Вт].

Коэффициент полезного действия представляет собой отношение отдаваемой мощности P_отд к подводимой мощности P_подв:

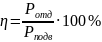. (3.4.4)

Часто бывает целесообразно определить КПД не как отношение мощностей, а как отношение работ (полезной работы к затраченной), особенно в тех случаях, когда работа над телом совершается не одновременно с работой, производимой самим телом, и с другой скоростью:

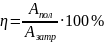. (3.4.5)

Вследствие неизбежных потерь КПД всегда меньше единицы:

η<1.

3. Законы сохранения

4.1. Импульс тела. Закон сохранения импульса

Импульс тела – физическая величина, равная произведению массы тела m на скорость его движения . Импульс тела – векторная величина. Вектор сонаправлен с вектором . Единица измерения: .

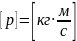Импульс одного тела: . (4.1.1)

Изменение импульса одного тела 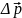: 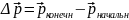. (4.1.2)

Вектор направлен из конца

вектора 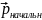в конец вектора

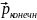
(рис. 4.1.1.)

Рис. 4.1.1

Импульс системы тел: 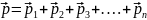. (4.1.3)

Закон сохранения импульса: 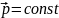. (4.1.4)

Импульс замкнутой системы тел не изменяется с течением времени

Закон сохранения импульса выполняется и для незамкнутой системы, если:

• геометрическая сумма внешних сил равна нулю,

• проекции внешних сил на направление движения равны нулю.

Для двух тел закон сохранения имеет вид 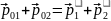(4.1.5)

(импульс системы двух тел до взаимодействия равен импульсу системы после взаимодействия).