Кинематика криволинейного движения материальной точки
Криволинейное движение в плоскости
Если телу сообщить начальную скорость υ0 под углом α к горизонту, то его движение будет криволинейным, поскольку его траекторией в данном случае является парабола. Это движение происходит в плоскости, поэтому для его описания необходимы две координаты. Такое движение можно представить двумя простыми движениями: равномерным по горизонтали (силой сопротивления воздуха можно пренебречь) и равноускоренным по вертикали (на тело действует сила тяжести). Движение тела вдоль оси OX описывается следующими законами:
.
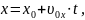
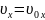(2.1.1)
Здесь x0 и x – координаты тела в начальный момент времени и в момент времени t соответственно; υ0x – проекция начальной скорости тела на ось OX; υx – проекция скорости тела на ось OX через время t.
Вдоль оси OY тело движется с ускорением свободного падения g. Движение описывается следующими уравнениями:
.
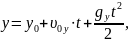
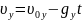(2.1.2)
Здесь y0 и y – координаты тела в начальный момент времени и в момент времени t соответственно; υ0y – проекция вектора начальной скорости тела на ось OY; υy –проекция скорости тела на ось OY через время t.
Из рис. 2.1.1 следует, что
.
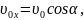
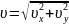(2.1.3)
Движение тела, брошенного под углом к горизонту
Рассмотрим движение, при котором точка бросания и точка падения тела находятся на одном уровне (рис. 2.1.2). Угол между вектором начальной скорости и горизонтом – α. Используя формулы (2.1.1), (2.1.2), (2.1.3) можно получить следующие выражения:
продолжительность
полета
,
(2.1.4)
дальность
полета
,
(2.1.5)
максимальная
высота подъема
.
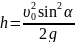(2.1.6)
Движение тела, брошенного горизонтально
Рассмотрим
движение, при котором точка бросания и
точка падения тела находятся на разных
уровнях (рис. 2.1.3). Угол между вектором
начальной скорости и горизонтом равен
нулю (вектор
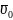параллелен оси OX)
. Используя тот же набор формул, что и
предыдущем случае, получим:
дальность
полета
,
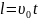(2.1.7)
в
ысота,
с которой брошено тело,
.
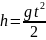(2.1.8)
Кинематика вращательного движения
Вращательным называется движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения. Для полного описания вращательного движения твердого тела достаточно описать вращение любой его точки, не лежащей на оси. Для описания движения материальной точки (центра масс абсолютно твердого тела) по окружности вводятся следующие физические величины:
Период вращения T – время, в течение которого точка совершает один полный оборот по окружности.
Частота вращения ν – число оборотов, совершаемых точкой за одну секунду. Период и частота вращения связаны как
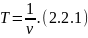
Средняя угловая скорость ω – физическая величина, равная отношению угла поворота Δφ (рис. 2.2.1) радиус-вектора за промежуток времени Δt к длительности этого промежутка:
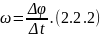
Мгновенная угловая скорость ω – физическая величина, равная пределу отношения угла поворота Δφ радиус-вектора точки за промежуток времени Δt к длительности этого промежутка:
Вектор
угловой скорости
направлен вдоль оси вращения по правилу
правого винта, т.е. его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности (рис. 2.2.2).
Угловая скорость ω связана следующими соотношениями:
с
линейной скоростью υ
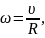(2.2.4)
с
линейной частотой ν
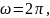(2.2.5)
с
периодом колебаний
Т
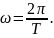(2.2.6)
Рис. 2.2.1 Рис. 2.2.2
Среднее угловое ускорение ε – физическая величина, равная отношению изменения угловой скорости за промежуток времени Δt к длительности этого промежутка:
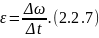
Мгновенное угловое ускорение ε: – физическая величина, равная пределу отношения изменения угловой скорости за промежуток времени Δt к длительности этого промежутка:
В
ектор
углового ускорения сонаправлен с
вектором угловой скорости в случае
равноускоренного движения (рис. 2.2.3, a)
и противоположно направлен ей в случае
равнозамедленного (рис. 2.2.3, b).
Угловое ускорение ε связано с тангенциальной составляющей линейного ускорения aτ соотношением:
.
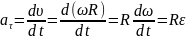(2.2.9)
Угловая скорость связана с нормальной составляющей ускорения линейного ускорения an:
.
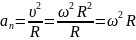(2.2.10)