4. Момент импульса

Моментом импульса точки (моментом количества движения точки) относительно некоторой неподвижной оси называется величина L, определяемая векторным произведением радиуса-вектора и импульса материальной точки:

. (5.4.1)

Направление совпадает с направлением поступательного движения правого винта при его вращении от к . Модуль момента импульса:

(5.4.2)

r и p – модули радиус-вектора и импульса соответственно; α – угол между радиус-вектором и вектором импульса.

Моментом импульса тела (моментом количества движения тела) относительно некоторой неподвижной оси называется величина L, равная сумме моментов импульсов всех N точек тела относительно этой оси:

(5.4.3)

Или момент импульса равен произведению момента инерции J тела на угловую скорость ω его движения вокруг этой оси:

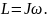(5.4.4)

С учетом момента импульса уравнение основного закона динамики вращательного движения принимает вид

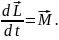(5.4.5)

Здесь  суммарный момент внутренних и внешних сил, действующих на тело ( = М_внутр + М_внеш). Суммарный момент всех внутренних сил взаимодействия частей тела относительно оси вращения всегда равен нулю, так как моменты внутренних сил взаимодействия частей тела попарно компенсируются и не приводят к изменению момента импульса тела. Если внешние силы отсутствуют или компенсируют друг друга (система является замкнутой), то и суммарный момент внешних сил равен нулю. Таким образом, из (5.4.5) следует закон сохранения момента импульса:

. (5.4.6)

6. Основы молекулярной физики

1. Основные положения молекулярно-кинетической теории. Основные определения и формулы

Молекулярно-кинетической теорией (МКТ) называется учение, которое объясняет строение и свойства тел движением и взаимодействием атомов и молекул, из которых состоят тела.

Основные положения МКТ:

1. Все тела состоят из частиц: молекул и атомов, в состав которых входят более мелкие элементарные частицы.

2. Частицы, из которых состоят тела, находятся в непрерывном хаотическом движении.

3. Между частицами любого тела существуют силы взаимодействия: притяжения и отталкивания.

Молекула – наименьшая устойчивая частица какого-либо вещества, обладающая его химическими свойствами. Молекула состоит из одного или нескольких атомов одинаковых или различных химических элементов.

Атом – наименьшая частица данного химического элемента; состоит из положительно заряженного ядра (соединенные протоны и нейтроны), вокруг которого на расстояниях, превышающих размер ядра более чем в 1000 раз, вращаются электроны. Атомы и молекулы электрически нейтральны.

Броуновское движение – непрерывное хаотическое движение частиц, помещенных в жидкость или газ в такие условия, при которых сила тяжести не влияет на их движение (взвешенные частицы). Причиной броуновского движения частиц являются непрерывные беспорядочные соударения этих частиц с молекулами жидкости (газа).

Постоянная Больцмана k = 1,38·10⁻²³ Дж/К.

Число Авогадро N_A = 6,02·10²³ моль⁻¹.

Универсальная газовая постоянная R = 8,31 Дж/моль·К.

R=kN_A . (6.1.1)

Количество вещества ν – физическая величина, характеризующая число структурных единиц в теле. Единицей измерения количества вещества является моль (моль). В одной структурной единице (в одном моле) содержится 6,02∙10²³ атомов (молекул). Такое число атомов называется числом Авогадро N_A.

Количество вещества равно отношению числа N атомов (молекул) в теле к числу Авогадро N_A или массы тела m к его молярной массе M:

или (6.1.2)

Молярная масса M – масса одного моля. Единица измерения молярной массы – килограмм на моль (кг/моль). Молярные массы веществ, молекулы которых состоят из одного атома, приведены в Периодической системе Менделеева в г/моль, что следует учитывать при решении задач.

Задача 6.1. На основе молярной массы и числа Авогадро рассчитать массу и размер одной молекулы вещества. Для определения массы воспользуемся соотношениями (6.1). Учитывая, что N = 1 получим формулу для массы молекулы:

.

Размер молекулы может быть оценен как размер a кубика, в котором содержится одна молекула (рис. 1):

А объем кубика V, в свою очередь, равен отношению массы молекулы m₀ к плотности вещества ρ:

Таким образом, получим формулу для расчета размера молекулы:

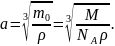
Рис. 1

Молярный объем – объем, занимаемый одним молем газа. Единица молярного объема – м³/моль:

. (6.1.3)

Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов:

(6.1.3)

Парциальное давление – давление, которое производил бы газ, входящий в состав газовой смеси, если бы он занимал объем, равный объему смеси при той же температуре.

Число степеней свободы i – число независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы.