
- •В ведение
- •Общие рекомендации
- •Список рекомендуемой литературы
- •Вопросы программы 2-й части курса математика
- •Раздел I. Функции двух и трех переменных
- •Раздел II. Неопределенные интегралы
- •Тема 1. Неопределенные интегралы
- •Тема 2. Определенный интеграл
- •Тема 3. Несобственные интегралы
- •Тема 4. Двойные интегралы
- •Тема 5. Криволинейные интегралы
- •Контрольная работа №3
- •Контрольная работа №4
- •Математика
- •3 94006, Воронеж, ул. 20-летия Октября, 84
Контрольная работа №4
Задача 1. Вычислить определенные интегралы.
1.
 2.
2.
 . 3.
. 3.
 .
.
4.
 .
5.
.
5.
 . 6.
. 6.
 .
.
7.
 . 8.
. 8.
 . 9.
. 9.
 .
.
10. . 11.
. 11.
 . 12.
. 12.
 .
.
13.
 . 14.
. 14.
 15.
15.
 .
.
16.
 . 17.
. 17.
 . 18.
. 18.
 .
.
19.
 . 20.
. 20.
 .
.
Задача 2. Вычислить несобственные интегралы или доказать их расходимость.
1.
 . 2.
. 2.
 . 3.
. 3.
 .
.
4.
 . 5.
. 5.
 . 6.
. 6.

 .
.
7.
 . 8.
. 8.
 . 9.
. 9.
 .
.
10.
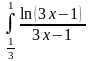 . 11.
. 11.
 . 12.
. 12.
 .
.
13.
 . 14.
. 14.
 15.
15.

16.
 . 17.
. 17.
 . 18.
. 18.

19.
 . 20.
. 20.
 .
.
Задача 3.
Вычислить площадь фигуры, ограниченной линиями, заданными в декартовой системе координат. Сделать чертеж.

Вычислить площадь фигуры, ограниченной линиями, заданными в декартовой системе координат. Сделать чертеж.

Вычислить площадь фигуры, ограниченной линиями, заданными в декартовой системе координат. Сделать чертеж.

4 . Вычислить площадь фигуры, ограниченной линиями, заданными в декартовой системе координат. Сделать чертеж.

5. Вычислить площадь фигуры, ограниченной линиями, заданными в декартовой системе координат. Сделать чертеж.

6. Вычислить объем тела, полученного при вращении фигуры, лежащей в плоскости XOY и ограниченной заданными линиями, вокруг оси ОХ.

7. Вычислить объем тела, полученного при вращении фигуры, лежащей в плоскости XOY и ограниченной заданными линиями, вокруг оси ОХ.

8. Вычислить объем тела, полученного при вращении фигуры, лежащей в плоскости XOY и ограниченной заданными линиями, вокруг оси ОХ.

9. Вычислить объем тела, полученного при вращении фигуры, лежащей в плоскости XOY и ограниченной заданными линиями, вокруг оси ОХ.

10. Вычислить длину дуги кривой, заданной уравнением параметрической форме.
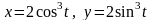
11. Вычислить длину дуги кривой, заданной уравнением в параметрической форме.

12. . Вычислить длину дуги кривой, заданной уравнением в параметрической форме.

13. . Вычислить длину дуги кривой, заданной уравнением в параметрической форме.

14.
. Найти длину
дуги кривой
 от точки
от точки
 до точки
до точки
 .
.
15.
Найти
длину дуги кривой
 ,
отсеченной осью Ox.
,
отсеченной осью Ox.
16.
Вычислить
длину дуги кривой, заданной уравнением
в полярных координатах

17.
Вычислить длину дуги кривой, заданной
уравнением в полярных координатах

18.
Вычислить длину дуги кривой, заданной
уравнением в полярных координатах

19.
. Вычислить длину дуги кривой, заданной
уравнением параметрической форме.
20.
. Вычислить длину дуги кривой, заданной
уравнением параметрической форме.
Задача
4. Вычислить
двойной интеграл
 по области D,
ограниченной указанными линиями:
по области D,
ограниченной указанными линиями:
1. f (x, y)= x2 + y; D : y = x2; x = y2
2. f (x, y) = xy; D : y = 3x; y = 2x; x=1
3.
f (x, y) = x + y; D : y =12 x; y = 3x
4. f (x, y) = x2y; D : y = 2 - x; y = x; x = 0
5. f (x, y) = x3- 2y; D : y = x2 – 1; x = 0; y = 0
6. f (x, y) = y + x; D : y = x; y =2 x, x=2
7. f (x, y) = 1 + y; D : y2 = x; y = x
8. f (x, y) = x -y; D : y = x2 – 1; y = - x2 + 1
9. f (x, y) = x(y – 1); D : y = 5x; y = x; x = 3
10. f (x, y) = (x – 2)y; D : y = x; y =2 x; x = 2.
 ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;  .
. ;
;

Задача 5. . Вычислить криволинейные интегралы
1. ,
где L
– дуга
кривой:
,
где L
– дуга
кривой:

2.
 где L
– дуга окружности x2+y2=4.
где L
– дуга окружности x2+y2=4.
3. где LOB
– отрезок прямой, соединяющей точки
O(0,
0) и B(2,
2).
где LOB
– отрезок прямой, соединяющей точки
O(0,
0) и B(2,
2).
4. где LАB
– отрезок прямой AB:
A(-1,0);
B(0,1).
где LАB
– отрезок прямой AB:
A(-1,0);
B(0,1).
5. где LАB
– отрезок прямой, заключенной между
точками A(0,
4) и B(4,
0).
где LАB
– отрезок прямой, заключенной между
точками A(0,
4) и B(4,
0).
6.
 ,
где L
– дуга
кардиоиды
,
где L
– дуга
кардиоиды

7. где L
– дуга
астроиды x
= cos3t,
y
= sin3t,
заключенной
между точками
A(1,
0); B(0,
1).
где L
– дуга
астроиды x
= cos3t,
y
= sin3t,
заключенной
между точками
A(1,
0); B(0,
1).
8.
 где L
– отрезок прямой
где L
– отрезок прямой
 соединяющий точки
соединяющий точки
A(0, -2) и B(4, 0).
9.
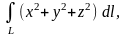 где L
– дуга кривой
где L
– дуга кривой

10.
 ,
где L
– дуга
кардиоиды:
,
где L
– дуга
кардиоиды:

11.
 где
LАB
– дуга параболы y
= x2
от
точки A(-1,
1) до точки
B(1,
1).
где
LАB
– дуга параболы y
= x2
от
точки A(-1,
1) до точки
B(1,
1).
12.
 ,
где LАB
– дуга астроиды: x
= cos3t;
y
= sin3t
от точки
A(2,
0) до точки
B(0,
2).
,
где LАB
– дуга астроиды: x
= cos3t;
y
= sin3t
от точки
A(2,
0) до точки
B(0,
2).
13.
 где
LOА
– дуга кубической параболы y
= x3
от
точки О(0, 0)
до точки
А(1, 1).
где
LOА
– дуга кубической параболы y
= x3
от
точки О(0, 0)
до точки
А(1, 1).
14.
 где L
– окружность x
= 2cost;
y
= 2sint,
при
положительном
направлении обхода.
где L
– окружность x
= 2cost;
y
= 2sint,
при
положительном
направлении обхода.
15.
 где L
– дуга эллипса: x
= 3cost;
y
= 2sint,
при
положительном
направлении обхода.
где L
– дуга эллипса: x
= 3cost;
y
= 2sint,
при
положительном
направлении обхода.
16.
 где LAB
– дуга
эллипса:
где LAB
– дуга
эллипса:
 от точки A(1,0)
до точки B(0,2).
от точки A(1,0)
до точки B(0,2).
17.
 где LOAB
– ломанная OAB:
O(0,0);
B(2,0);
A(2,1).
где LOAB
– ломанная OAB:
O(0,0);
B(2,0);
A(2,1).
18.
 где LAB
– отрезок прямой AB:
A(1,1);
B(3,4).
где LAB
– отрезок прямой AB:
A(1,1);
B(3,4).
19.
 где LAB
– отрезок прямой AB:
где LAB
– отрезок прямой AB:

20.
 где LAB
– отрезок прямой AB:
A(1,2);
B(3,6).
где LAB
– отрезок прямой AB:
A(1,2);
B(3,6).
Оглавление
Введение……………………….………………………………………...... |
3 |
Общие рекомендации…………………….……………………………… |
3 |
Список рекомендуемой литературы…….………………………………. |
4 |
Вопросы программы к контрольной работе №3,4……………………………………………………………………… |
4 |
|
|
Контрольная работа № 3…………………………………………………. |
5 |
Контрольная работа № 4…………………………………………………. |
7 |
