
- •Двойные интегралы.
- •Основные понятия и свойства.
- •Вычисление двойных интегралов с помощью повторного интегрирования
- •Геометрические приложения двойных интегралов
- •Тройной интеграл
- •Замена переменных в тройном интеграле
- •Тройной интеграл в цилиндрических координатах
- •2. Тройной интеграл в сферической системе координат
- •Приложения тройных интегралов
- •Криволинейный интеграл 2-го рода
- •1. Задача, приводящая к понятию криволинейного интеграла 2-го рода.
- •2. Определение криволинейного интеграла 2-го рода.
- •3. Свойства криволинейного интеграла 2-го рода
- •5.Формула Грина
- •6.Условия независимости криволинейного интеграла от пути интегрирования
- •7. Нахождение функции по ее полному дифференциалу
- •394026 Воронеж, Московский просп., 14
Замена переменных в тройном интеграле
Тройной интеграл в цилиндрических координатах
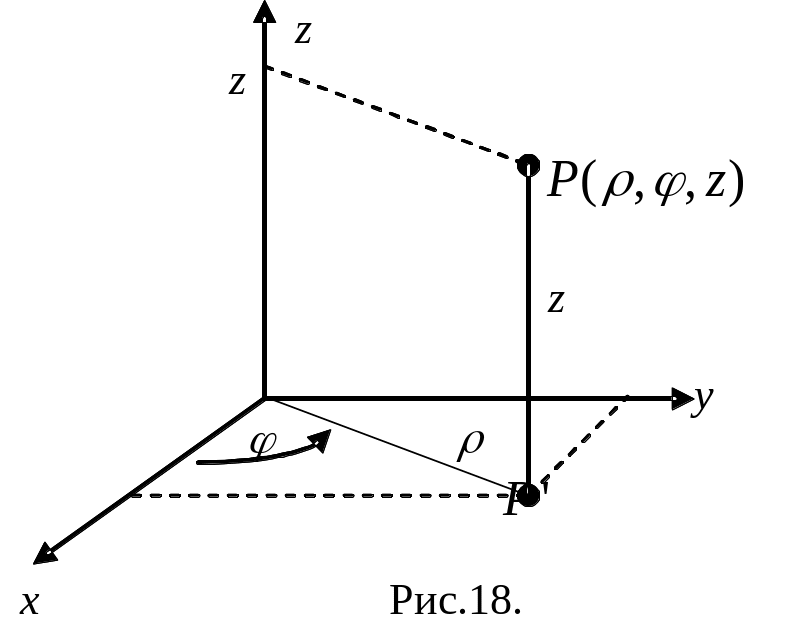
Пусть
-
произвольная точка в пространстве,![]() -
проекция точки
-
проекция точки
![]() на плоскость
.
В цилиндрических координатах положение
точки
в пространстве определяется тремя
числами
на плоскость
.
В цилиндрических координатах положение
точки
в пространстве определяется тремя
числами
![]() где
где
![]() -
полярные координаты точки
на плоскости
,
-
полярные координаты точки
на плоскости
,
![]() -
аппликата точки
(рис.18). Переход от прямоугольных координат
-
аппликата точки
(рис.18). Переход от прямоугольных координат
![]() к цилиндрическим
к цилиндрическим
![]() задается формулами
задается формулами
![]()
![]()
![]()
![]() Заметим, что при переходе к цилиндрическим
координатам
Заметим, что при переходе к цилиндрическим
координатам
![]() Элемент площади в полярных координатах
находился по формуле
Элемент площади в полярных координатах
находился по формуле![]() ,
поэтому элемент объема в цилиндрической
системе координат имеет вид
,
поэтому элемент объема в цилиндрической
системе координат имеет вид
![]() или
или
![]()
Следовательно, справедливы равенства
=![]() =
=
=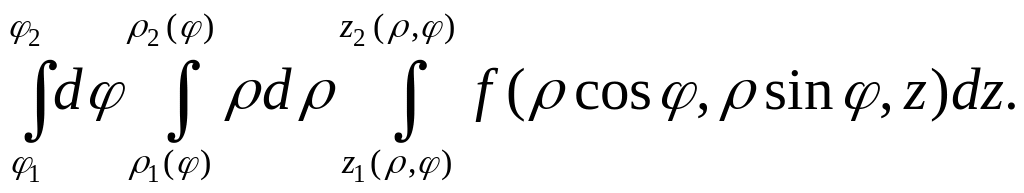
 Пример. Вычислить
объем, ограниченный поверхностями
Пример. Вычислить
объем, ограниченный поверхностями
![]() (рис.19).
(рис.19).
Решение.
Переведем уравнения поверхностей в
цилиндрические координаты. Уравнение
цилиндрической поверхности примет вид
![]() или
или![]() .
Уравнение параболоида
.
Уравнение параболоида
![]() На
плоскость
область проектируется в круг радиуса
На
плоскость
область проектируется в круг радиуса![]() .
Тогда
.
Тогда
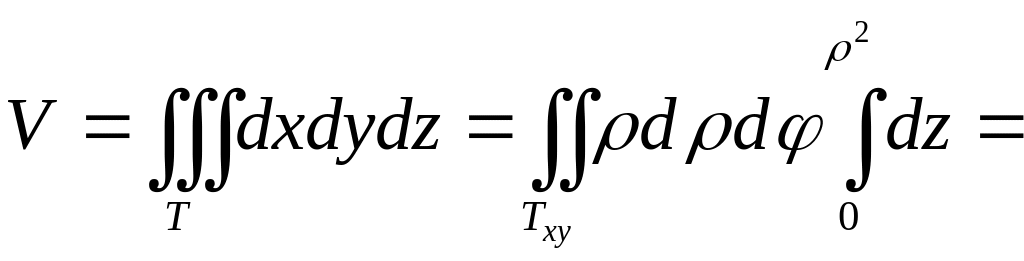
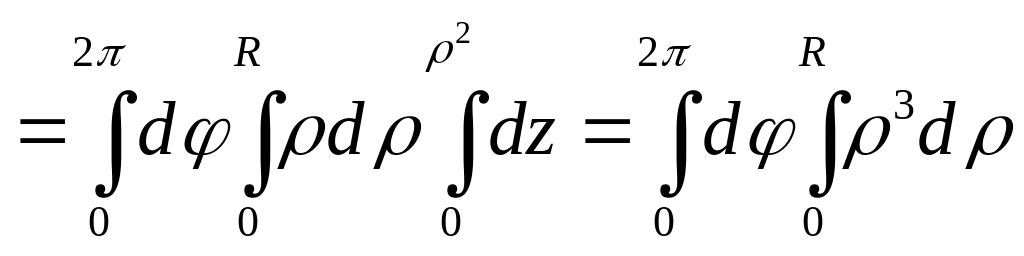
![]()
![]()
![]()
2. Тройной интеграл в сферической системе координат
Пусть - произвольная точка в пространстве
-
проекция точки
на плоскость
.
В сферических координатах положение
точки
в пространстве определяется тремя
числами
![]() где
где
![]() -
расстояние точки
от точки
-
расстояние точки
от точки
![]() (начала координат),
(начала координат),
![]() -
угол между лучами
и
-
угол между лучами
и![]() ,
-
,
-
п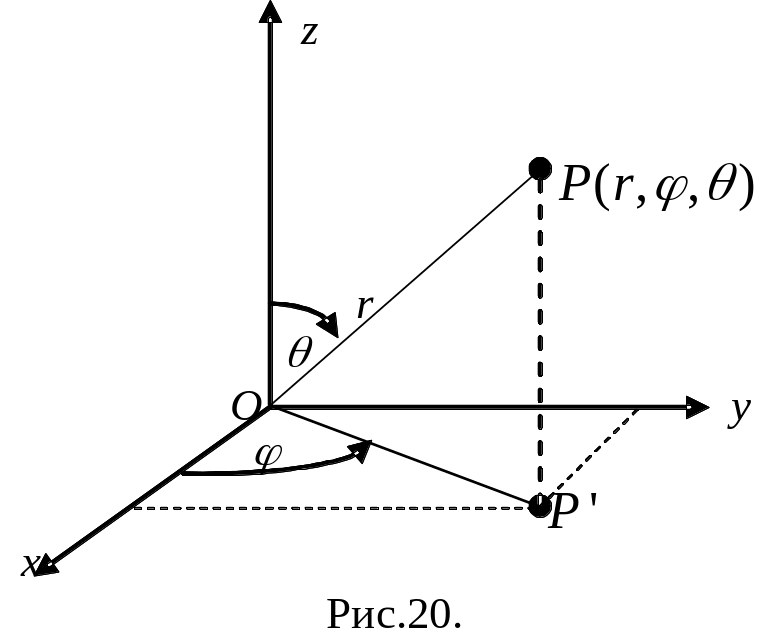 олярный
угол точки
на плоскости
(рис.20). Переход от прямоугольных координат
к
сферическим
олярный
угол точки
на плоскости
(рис.20). Переход от прямоугольных координат
к
сферическим
![]() задается формулами
задается формулами
![]()
![]()
![]()
![]()
![]()
![]() Элемент объема в
сферической системе координат имеет
вид
Элемент объема в
сферической системе координат имеет
вид
![]() или
или
![]()
При
переходе к сферическим координатам
![]()
Следовательно, справедливы равенства =
=![]()
=
Пример.
Вычислить интеграл![]() ,
где область
ограничена сферой
,
где область
ограничена сферой
![]() и конусом
и конусом
![]() (внутри конуса) (рис.21).
(внутри конуса) (рис.21).
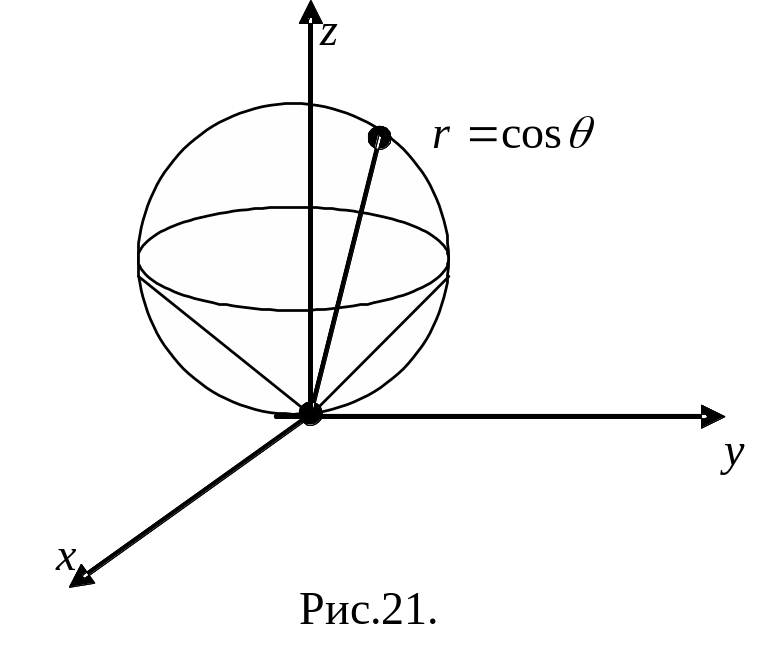 Решение. Приведем
уравнение сферы к виду
Решение. Приведем
уравнение сферы к виду
![]()
получим
уравнение сферы радиуса ½ с центром в
точке (0,0,1/2) . В сферической системе
координат уравнение сферы принимает
вид![]() ,
тогда
,
тогда
=![]() =
=
=![]()
![]()
![]()
Приложения тройных интегралов
1.Объем пространственной области
2. Масса тела, занимающего область ,
, где - объемная плотность распределения массы в точке тела.
3.Статические моменты тела относительно координатных плоскостей:
![]()
![]() .
.
4.
Координаты центра тяжести
![]() тела
тела
![]() ,
,
где
![]() -
статические моменты тела относительно
координатных плоскостей.
-
статические моменты тела относительно
координатных плоскостей.
5.
Моменты инерции тела относительно осей
![]() и начала координат
и начала координат
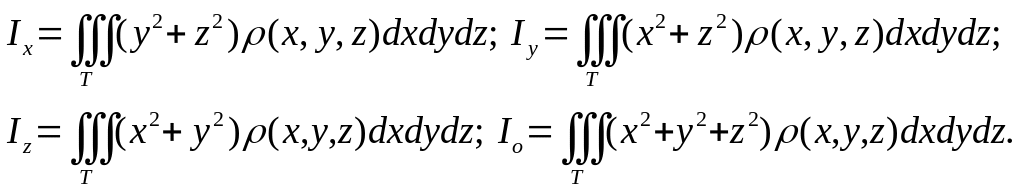
Задачи для самостоятельного решения
1. Вычислить тройные интегралы:
а)![]() ;
б)
;
б)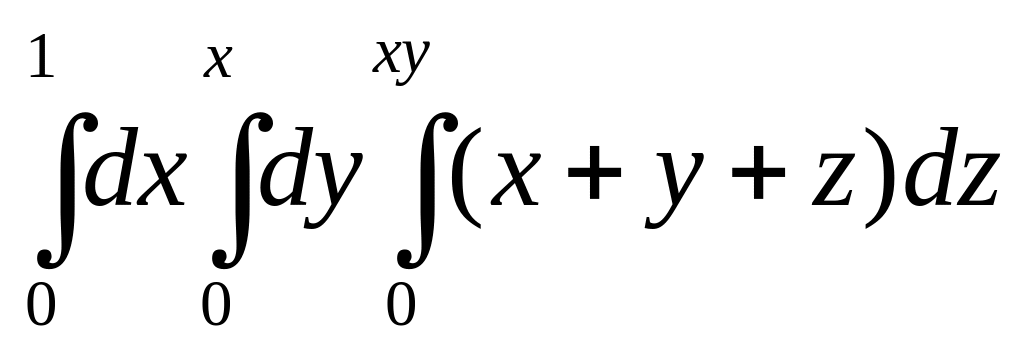 ;
в)
;
в)
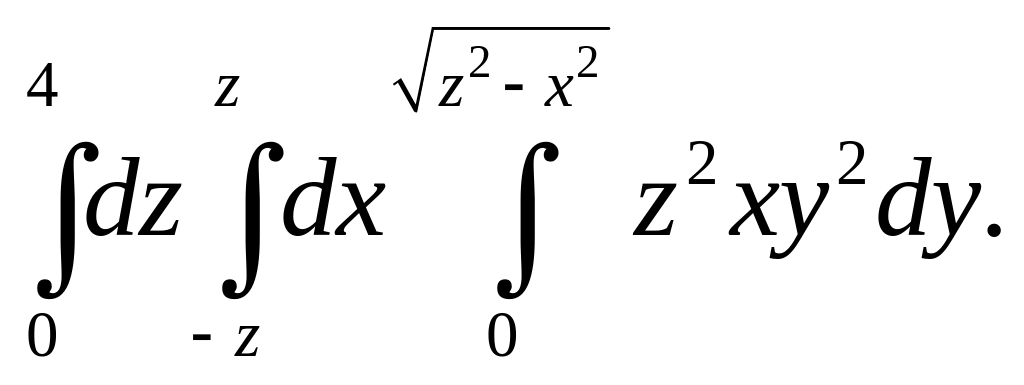
2.Расставить всеми возможными способами пределы интегрирования в следующих тройных интегралах в декартовой системе координат:
а) ;
б)
;
б) ;
;
в) ;
г)
;
г)
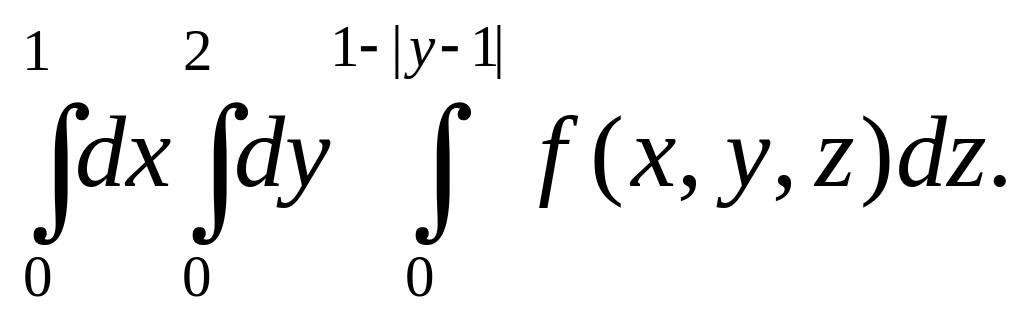
3.
Расставить пределы интегрирования в
цилиндрической системе координат в
интеграле![]() ,
если:
,
если:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
4. Расставить пределы интегрирования в сферической системе координат в интеграле , если:
а)
![]()
б)
![]()
5. Вычислить:
а)
![]()
б)
![]()
в)![]()
![]() ;
;
г)
![]()
6. Найти объем следующих тел:
а)
![]()
б)
![]()
7. Найти массу тела, ограниченного поверхностями
![]() ,
если плотность тела изменяется по
закону: а)
;
б)
,
если плотность тела изменяется по
закону: а)
;
б)
![]() в)
в)![]() .
.
Ответ:
а)![]() б)
б)
![]() в)
в)
![]()
8. Найти координаты центра тяжести однородного тела, ограниченного поверхностями:
а)
![]()
б)
![]()
в)
![]()
г)
![]()
![]()
Ответ:
а)![]() б)
б)![]() в)
в)![]() г)
г)![]()
9.
Найти координаты центра тяжести тела,
ограниченного поверхностями
![]() если плотность тела изменяется по
закону: а)
если плотность тела изменяется по
закону: а)
![]()
б)
![]() в)
в)
![]()
Ответ:
а)
![]() б)
б)
![]()
в)![]()
10.
Найти моменты инерции относительно
координатных плоскостей однородного
тела плотности![]() ,
ограниченного поверхностями:
,
ограниченного поверхностями:
а)
![]()
б)
![]()
в)![]() .
.
Ответ:
а)
![]()
![]() б)
б)![]()
в)
![]()
11.
Найти моменты инерции относительно
координатных плоскостей тела: а)
плотности![]() ,
ограниченного поверхностью:
,
ограниченного поверхностью:
б)
плотности
![]() ограниченного поверхностями
ограниченного поверхностями
![]() ,
,
![]()
Ответ:
а)
![]()
![]() б)
б)![]()
12. Найти моменты инерции относительно осей координат и начала координат однородного тела плотности , ограниченного поверхностями:
а)
б)
![]()
Ответ:
а)
![]()
б)![]()
![]()
13.
Определить момент инерции относительно
начала координат тела плотности
![]() где
где![]() ,
ограниченного поверхностью
,
ограниченного поверхностью
![]()
Ответ:
![]()
14.
Пусть
-
однородный цилиндр плотности
с высотой
и радиусом основания
.
Найти силу притяжения этим цилиндром
материальной точки массы![]() ,
находящейся в
,
находящейся в
центре основания цилиндра.
Ответ:![]()
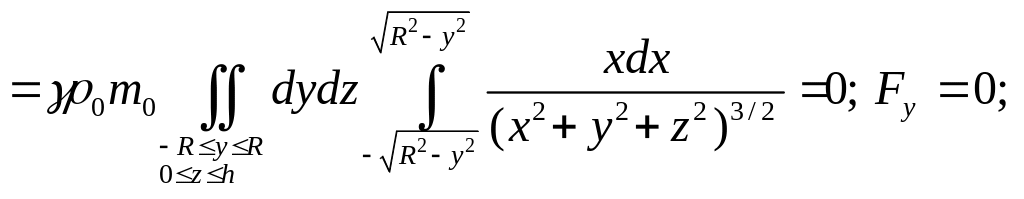
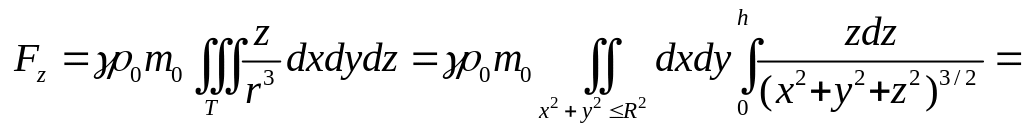
![]()
![]()
