
- •Двойные интегралы.
- •Основные понятия и свойства.
- •Вычисление двойных интегралов с помощью повторного интегрирования
- •Геометрические приложения двойных интегралов
- •Тройной интеграл
- •Замена переменных в тройном интеграле
- •Тройной интеграл в цилиндрических координатах
- •2. Тройной интеграл в сферической системе координат
- •Приложения тройных интегралов
- •Криволинейный интеграл 2-го рода
- •1. Задача, приводящая к понятию криволинейного интеграла 2-го рода.
- •2. Определение криволинейного интеграла 2-го рода.
- •3. Свойства криволинейного интеграла 2-го рода
- •5.Формула Грина
- •6.Условия независимости криволинейного интеграла от пути интегрирования
- •7. Нахождение функции по ее полному дифференциалу
- •394026 Воронеж, Московский просп., 14
Тройной интеграл
Основные определения и теоремы для тройных интегралов аналогичны соответствующим определениям и теоремам для двойных интегралов.
Пусть
-
область в трехмерном евклидовом
пространстве , ограниченная замкнутой
поверхностью, и пусть в области
и на ее границе определена непрерывная
функция![]() .
Разобьем область
на
частей так, чтобы любые две части не
имели общих внутренних точек, в каждой
части
.
Разобьем область
на
частей так, чтобы любые две части не
имели общих внутренних точек, в каждой
части
![]() возьмем произвольную точку
возьмем произвольную точку
![]() и составим интегральную сумму вида
и составим интегральную сумму вида
![]() где
где
![]() - объем части
- объем части
![]() Пусть
-
диаметр
,
,
Пусть
-
диаметр
,
,![]() .
.
Определение.
Если существует предел последовательности
интегральных сумм
при
,
и если предел не зависит ни от способа
разбиения области
на
части![]() ,
ни от выбора точек
,
ни от выбора точек![]() ,
то он называется тройным
интегралом
от функции
,
то он называется тройным
интегралом
от функции
![]() по области
и обозначается
по области
и обозначается
![]() или
или
![]() ,
то есть
,
то есть
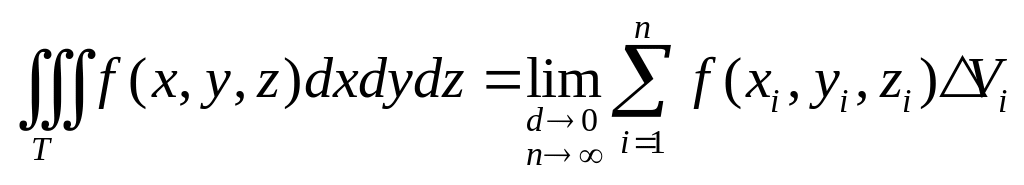 .
.
Теорема (достаточные условия существования тройного интеграла). Если функция непрерывна в области , ограниченной замкнутой поверхностью, то она интегрируема в этой области.
В дальнейшем будем предполагать, что условия этой
теоремы выполнены.
Из определения тройного интеграла следует, что объем
области
:
![]()
Физический
смысл тройного интеграла - масса тела,
занимающего область
с объемной плотностью, то есть если
![]() -
объемная плотность распределения массы
в точке
-
объемная плотность распределения массы
в точке
![]() тела, то масса тела
тела, то масса тела
![]() .
.
Тройные интегралы обладают такими же свойствами, как определенные и двойные интегралы (линейность, аддитивность, формулы среднего значения и т.д.)
Вычисление тройных интегралов с помощью повторного интегрирования.
Назовем трехмерную область , ограниченную замкнутой поверхностью правильной, если:
1) всякая прямая, параллельная оси , проведенная через внутреннюю точку области пересекает поверхность в двух точках;
2) вся область проектируется на плоскость в правильную (двумерную) область ;
3) всякая часть области , отсеченная плоскостью, параллельной любой из координатных плоскостей, также обладает свойствами 1),2).
Пусть
функция
![]() определена и непрерывна в области
определена и непрерывна в области![]() ,
где
,
где
![]() и
и
![]() -
непрерывные функции в ограниченной
замкнутой области
.
Обозначим
-
непрерывные функции в ограниченной
замкнутой области
.
Обозначим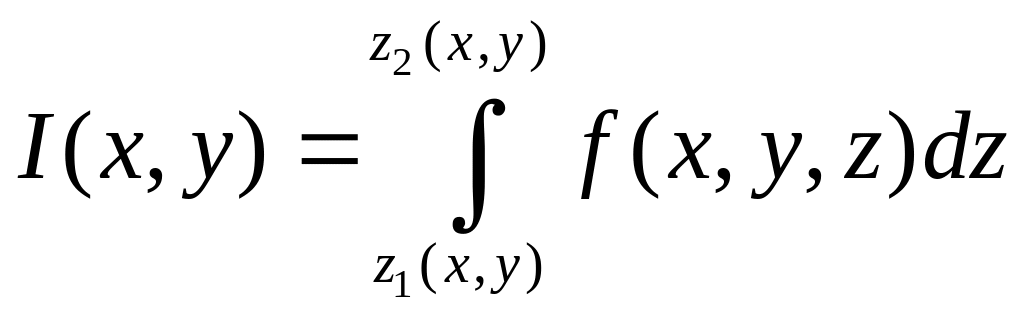 .
.
Назовем повторным интеграл вида
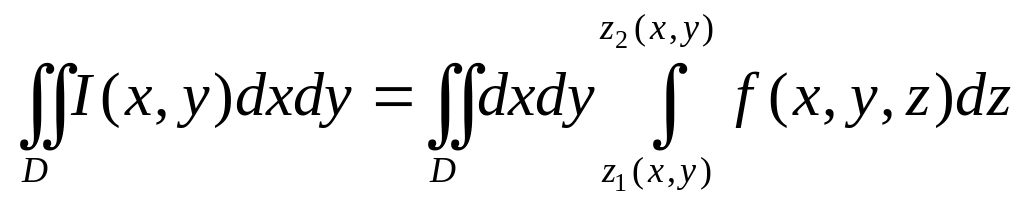 .
.
Теорема. Тройной интеграл от непрерывной функции
по правильной области равен повторному
интегралу
=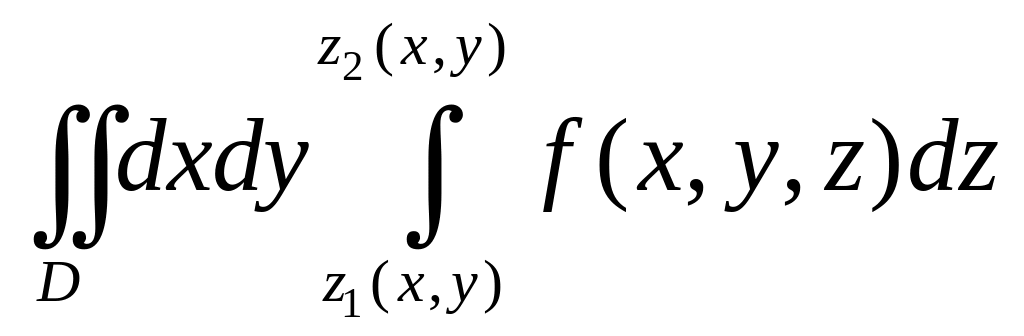 .
.
Если
область
правильная в направлении оси
,
то есть![]() ,
то двойной интеграл
,
то двойной интеграл
![]() в свою очередь можно свести к повторному,
тогда
в свою очередь можно свести к повторному,
тогда
=
Таким образом, вычисление тройного интеграла сводится в этом случае к последовательному вычислению трех определенных (однократных) интегралов:
=
Пример.
Вычислить интеграл
![]() ,
где
,
где
![]() область ограниченная поверхностями
область ограниченная поверхностями
![]()
![]()
Решение. Область можно представить в виде
![]() ,
,
где![]() .
Сводя тройной интеграл к повторному,
получим
.
Сводя тройной интеграл к повторному,
получим
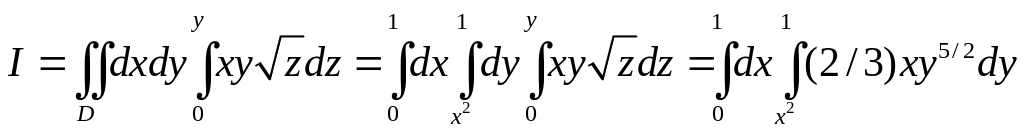 =
=
![]()
