
- •Двойные интегралы.
- •Основные понятия и свойства.
- •Вычисление двойных интегралов с помощью повторного интегрирования
- •Геометрические приложения двойных интегралов
- •Тройной интеграл
- •Замена переменных в тройном интеграле
- •Тройной интеграл в цилиндрических координатах
- •2. Тройной интеграл в сферической системе координат
- •Приложения тройных интегралов
- •Криволинейный интеграл 2-го рода
- •1. Задача, приводящая к понятию криволинейного интеграла 2-го рода.
- •2. Определение криволинейного интеграла 2-го рода.
- •3. Свойства криволинейного интеграла 2-го рода
- •5.Формула Грина
- •6.Условия независимости криволинейного интеграла от пути интегрирования
- •7. Нахождение функции по ее полному дифференциалу
- •394026 Воронеж, Московский просп., 14
Геометрические приложения двойных интегралов
1.
Площадь
![]() области
на плоскости
выражается формулой
области
на плоскости
выражается формулой
![]()
2.
Объем
тела![]() ,
где
,
где
![]() непрерывная
неотрицательная в области
непрерывная
неотрицательная в области
функция,
выражается формулой
![]()
3.
Площадь поверхности, заданной явно
уравнением
![]() ,
вычисляется с помощью двойного интеграла
вида:
,
вычисляется с помощью двойного интеграла
вида:
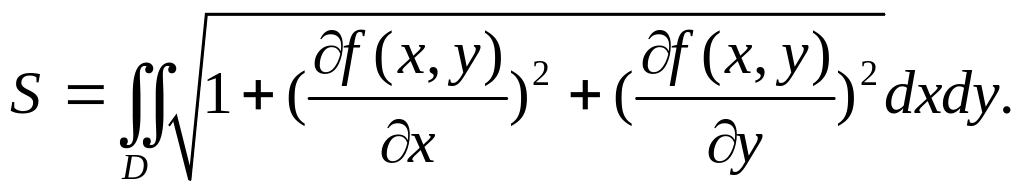
Физические приложения двойных интегралов
Пусть - материальная бесконечно тонкая пластинка с плотностью . Тогда справедливы следующие формулы:
1.![]() - масса пластинки;
- масса пластинки;
2.
![]() -
статические моменты пластинки относительно
осей
-
статические моменты пластинки относительно
осей
![]()
3.
![]() -
координаты центра тяжести пластинки;
-
координаты центра тяжести пластинки;
4.
![]() -
моменты инерции пластинки относительно
осей
-
моменты инерции пластинки относительно
осей
5.
![]() -
момент инерции пластинки относительно
начала координат.
-
момент инерции пластинки относительно
начала координат.
Пример.
Найти объем тела![]() ,
ограниченного поверхностями
,
ограниченного поверхностями
![]()
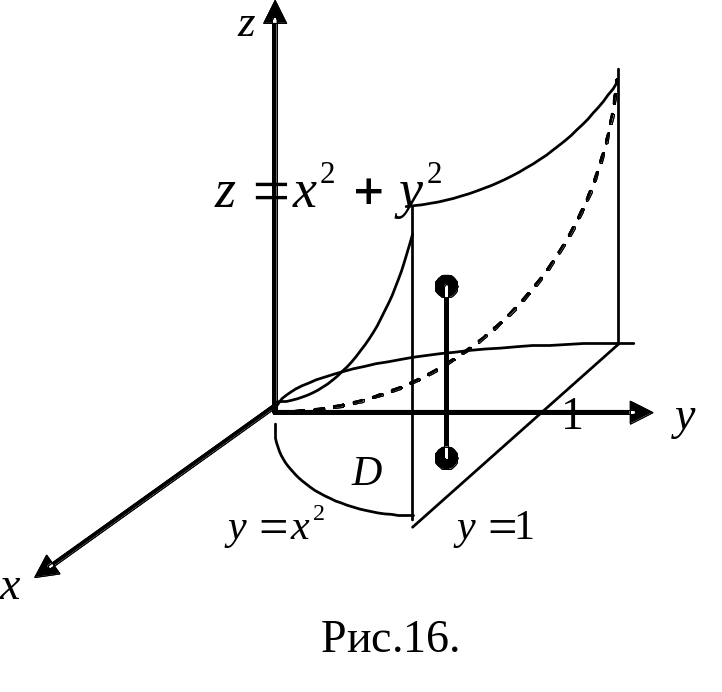
Решение. Данное тело можно представить в виде
![]() (рис.16), где
-
область на плоскости
,
ограниченная кривыми
(рис.16), где
-
область на плоскости
,
ограниченная кривыми![]() ,
то есть
,
то есть
![]()
 .
Переходя от двойного интеграла к
повторному, получим
.
Переходя от двойного интеграла к
повторному, получим
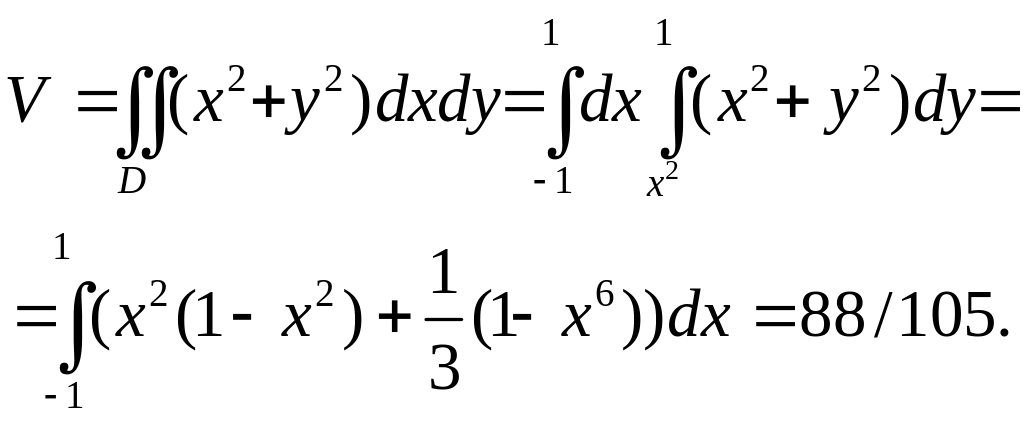
Пример.
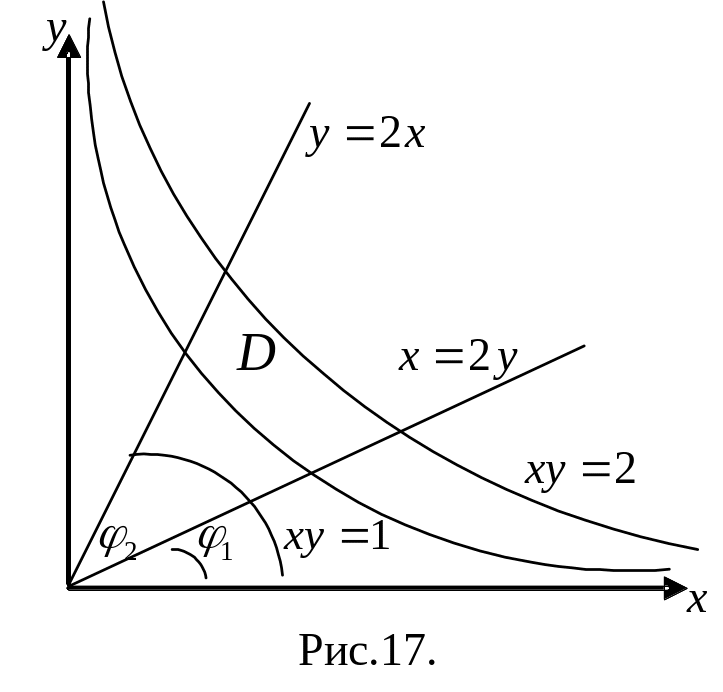
Найти моменты инерции
![]() относительно осей
относительно осей
![]() пластины с плотностью
пластины с плотностью
![]() ограниченной кривыми
ограниченной кривыми
![]() и
прямыми
и
прямыми
![]() ,
расположенной в первом квадранте
(рис.17).
,
расположенной в первом квадранте
(рис.17).
 Решение.
Решение.
![]()
![]() .
Чтобы свести каждый из этих интегралов
к повторному в декартовых координатах,
нужно область
разбить на три части. Поэтому удобнее
перейти к полярным координатам:
.
Чтобы свести каждый из этих интегралов
к повторному в декартовых координатах,
нужно область
разбить на три части. Поэтому удобнее
перейти к полярным координатам:
![]()
![]() .
Тогда
изменяется от
.
Тогда
изменяется от
![]() до
до![]() ,
а при каждом значении
,
а при каждом значении
![]() переменная
изменяется от
переменная
изменяется от
![]() (значение
на
кривой
(значение
на
кривой![]() ,
уравнение которой в полярных координатах
в I
квадранте имеет вид
,
уравнение которой в полярных координатах
в I
квадранте имеет вид
![]() )
до
)
до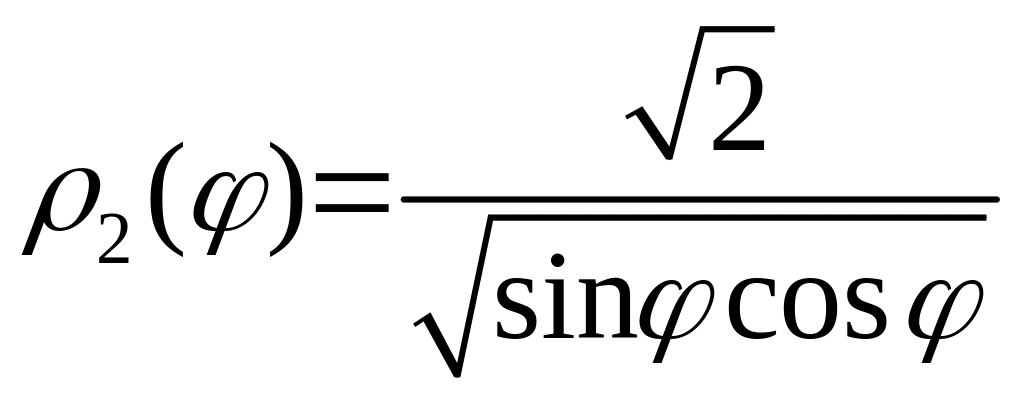 (значение
на кривой
(значение
на кривой
![]() Следовательно,
Следовательно,
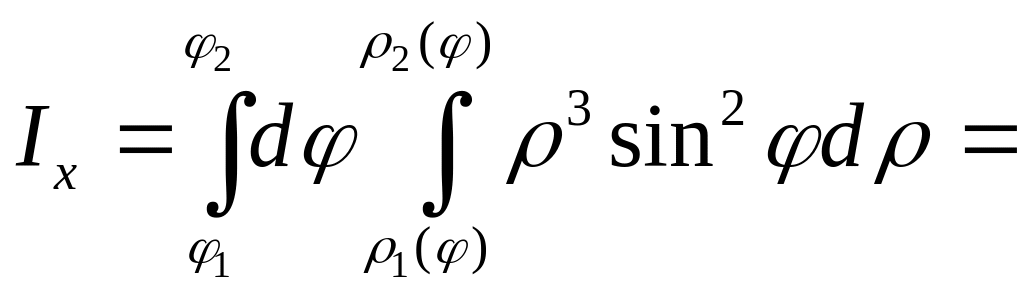
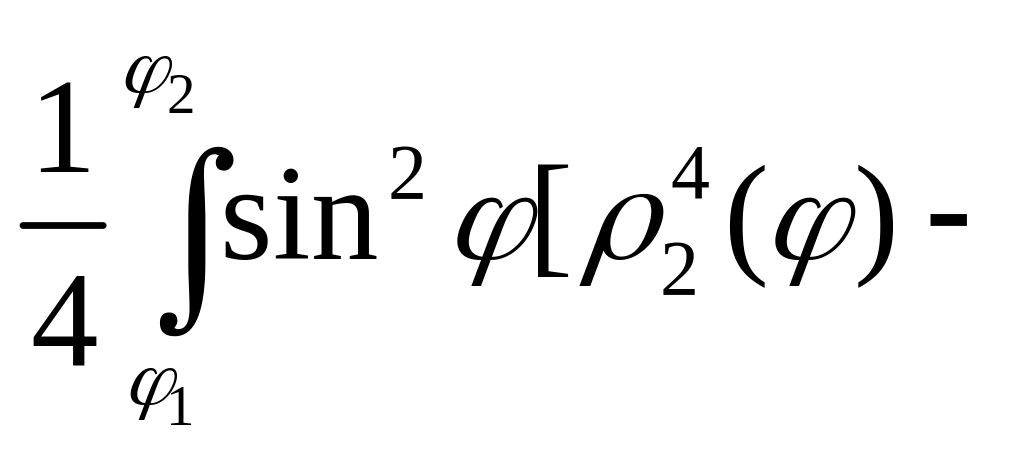
![]()
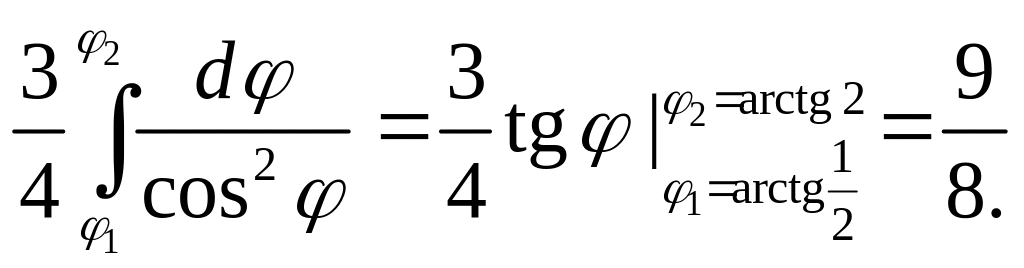 Аналогично
получаем
Аналогично
получаем
![]()
Задачи для самостоятельного решения
1. Привести двойной интеграл к повторному двумя способами, если:
а)
-
область, ограниченная кривыми
![]()
б)
-
круг
![]()
в) - треугольник со сторонами, лежащими на прямых
![]()
г)
-
кольцо
![]()
д)
-
область, ограниченная кривыми
![]()
![]() ;
;
е)
-
область, лежащая вне окружности и внутри
кривой![]() .
.
2. Изменить порядок интегрирования в повторных интегралах:
а)
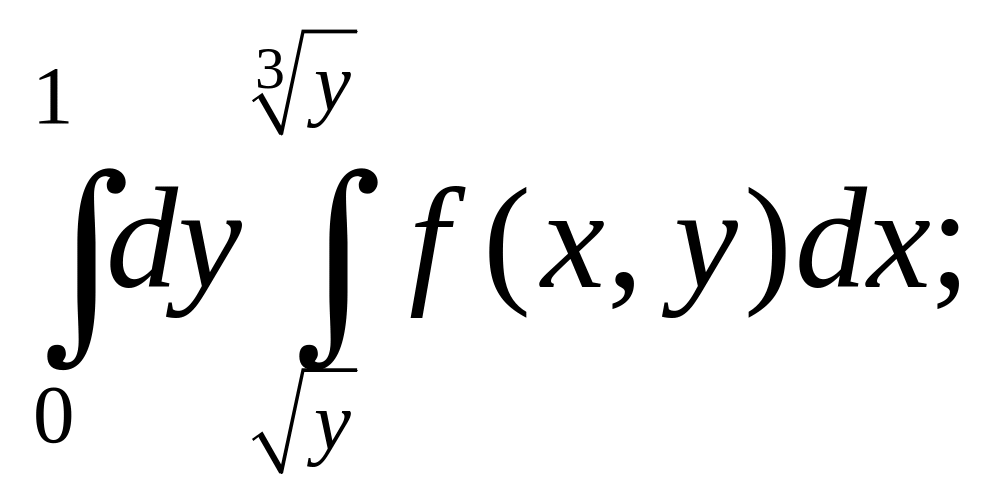 б)
б)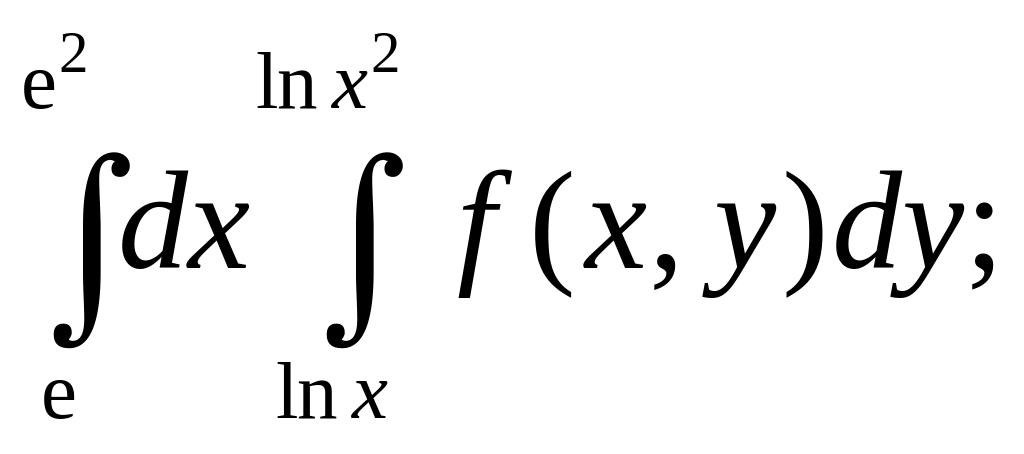 в)
в)![]()
г)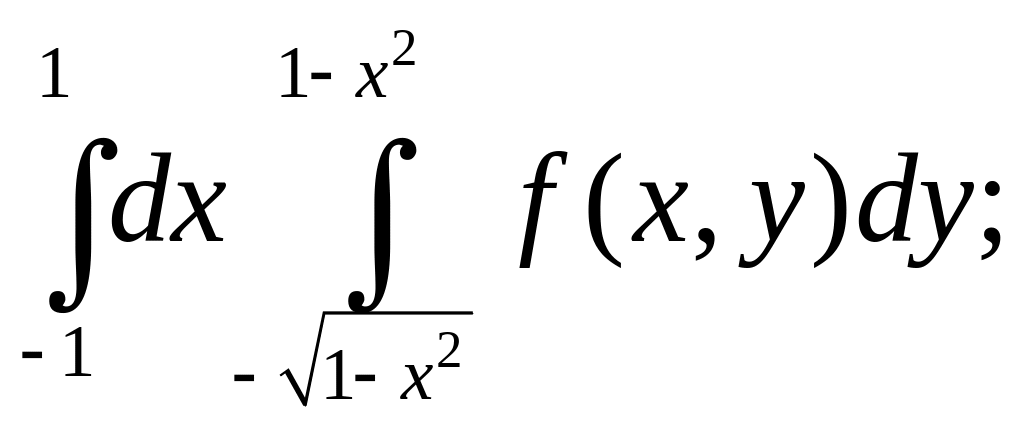 д)
д)
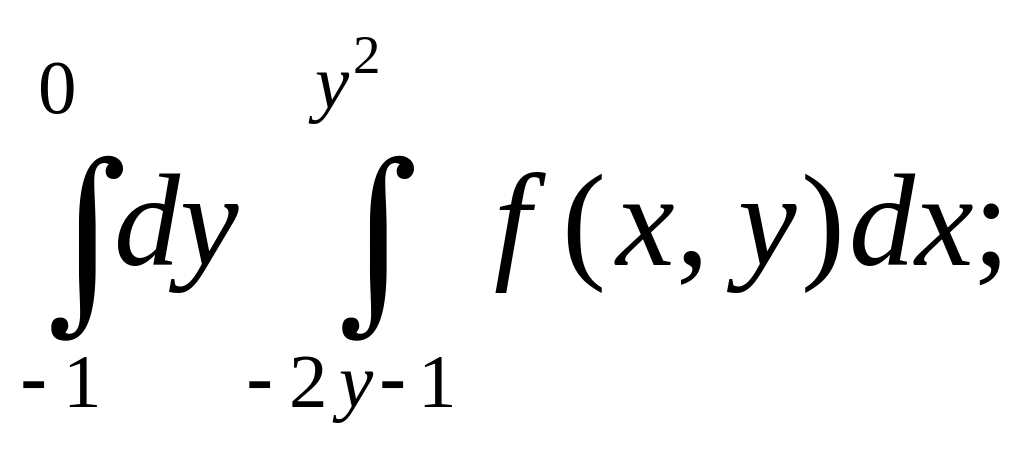
е)
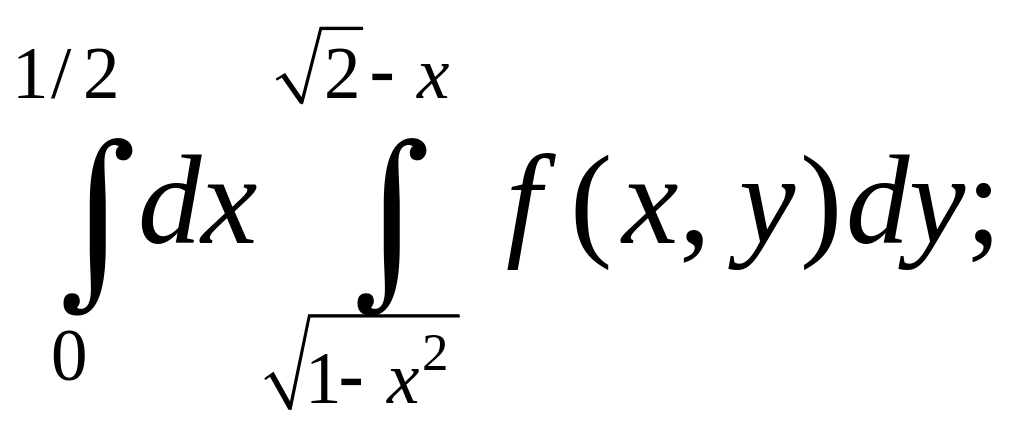 ж)
ж)
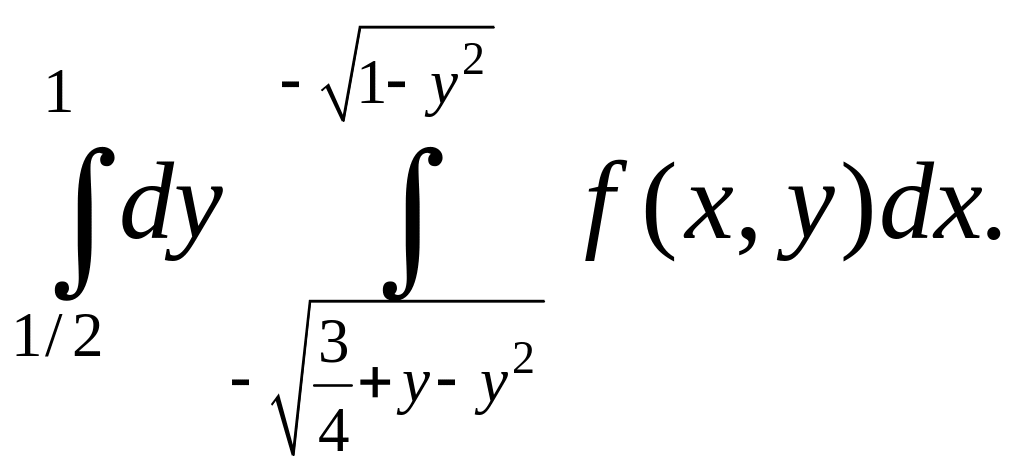
3. Вычислить двойные интегралы:
а)![]() б)
б)
![]()
в)
![]() где
где
![]()
г)
![]() где
где
![]()
д)
![]() где
где
![]()
е)![]() где
-
область, ограниченная кривыми
где
-
область, ограниченная кривыми
![]()
![]() ;
;
ж) где - область, ограниченная кривой
![]()
з)
![]() где
-
область, ограниченная кривыми
где
-
область, ограниченная кривыми
![]()
4. В следующих интегралах перейти к полярным координатам
а)![]() б)
б)
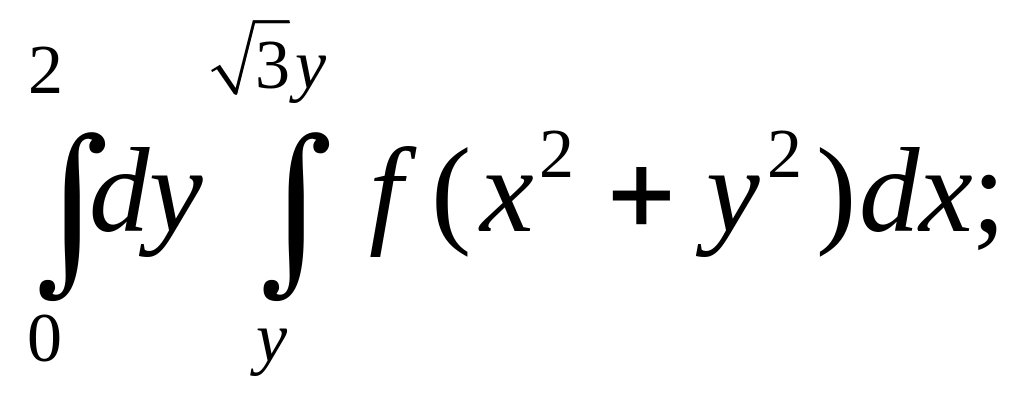 в)
в)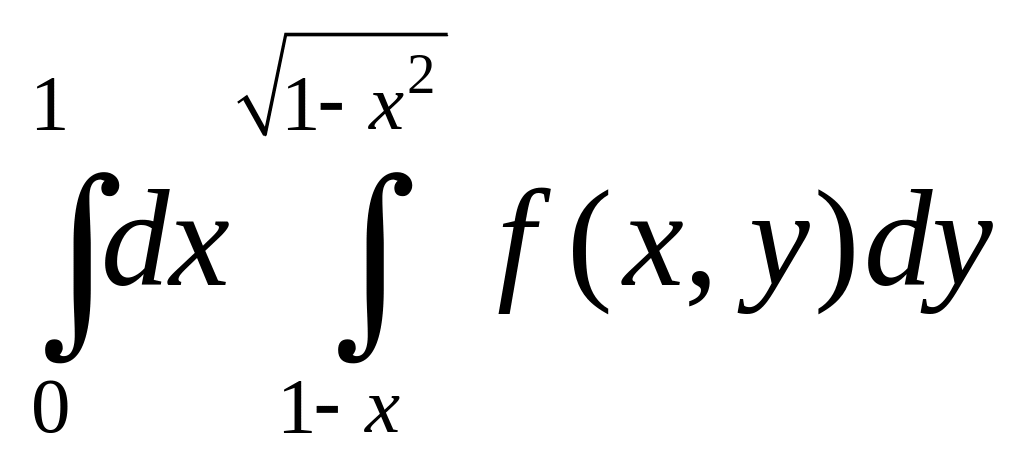 .
.
5. Вычислить объем тела, ограниченного поверхностями:
а)![]()
б)
![]()
в)
![]()
6. Найти координаты центра тяжести однородной пластинки, ограниченной кривыми:
а)
![]()
б)
![]()
в)
![]()
Ответ:
а)
![]() б)
б)![]() в)
в)![]()
7.
Найти координаты центра тяжести круглой
пластинки
![]() если ее плотность в точке
если ее плотность в точке
![]() пропорциональна расстоянию от точки
до точки
пропорциональна расстоянию от точки
до точки
![]()
Ответ:
![]()
8.
Найти моменты инерции
![]() и
и
![]() относительно осей
относительно осей
и
однородной пластинки с плотностью![]() ,
ограниченной кривыми:
,
ограниченной кривыми:
а)
![]()
б)
![]()
в)
![]()
г)![]()
Ответ:
а)
![]() б)
б)![]() в)
в)
![]() г)
г)![]()
9.
Найти моменты инерции
и
относительно осей
и
однородной пластинки с плотностью![]() ,
ограниченной кривыми:
,
ограниченной кривыми:
а)
б)
![]()
Ответ:
а)![]() б)
б)
![]()
10.
Шар радиуса
![]() погружен в жидкость постоянной плотности
,
причем центр шара находится на расстоянии
погружен в жидкость постоянной плотности
,
причем центр шара находится на расстоянии
![]() от уровня жидкости и
от уровня жидкости и![]() .
Найти силы давления
.
Найти силы давления![]() и
и
![]() на верхнюю и нижнюю полусферы этого
шара.
на верхнюю и нижнюю полусферы этого
шара.
Ответ:![]()
11.
Доказать, что если в плоскости, где
расположена пластинка
массы
,
взяты две параллельные оси
и
![]() на расстоянии
друг от друга, причем первая из них
проходит через центр тяжести пластинки
,
то моменты инерции пластинки
относительно этих осей связаны
соотношением
на расстоянии
друг от друга, причем первая из них
проходит через центр тяжести пластинки
,
то моменты инерции пластинки
относительно этих осей связаны
соотношением
![]()
Ответ: Взяв ось в качестве оси абсцисс, получаем
![]()
Так
как, по условию![]() ,
то приходим к равенству
,
то приходим к равенству
