
- •Двойные интегралы.
- •Основные понятия и свойства.
- •Вычисление двойных интегралов с помощью повторного интегрирования
- •Геометрические приложения двойных интегралов
- •Тройной интеграл
- •Замена переменных в тройном интеграле
- •Тройной интеграл в цилиндрических координатах
- •2. Тройной интеграл в сферической системе координат
- •Приложения тройных интегралов
- •Криволинейный интеграл 2-го рода
- •1. Задача, приводящая к понятию криволинейного интеграла 2-го рода.
- •2. Определение криволинейного интеграла 2-го рода.
- •3. Свойства криволинейного интеграла 2-го рода
- •5.Формула Грина
- •6.Условия независимости криволинейного интеграла от пути интегрирования
- •7. Нахождение функции по ее полному дифференциалу
- •394026 Воронеж, Московский просп., 14
Вычисление двойных интегралов с помощью повторного интегрирования
Пусть функция определена в области
![]() ,
,
где![]() и
и
![]() -
непрерывные функции на отрезке
-
непрерывные функции на отрезке
![]() .
.
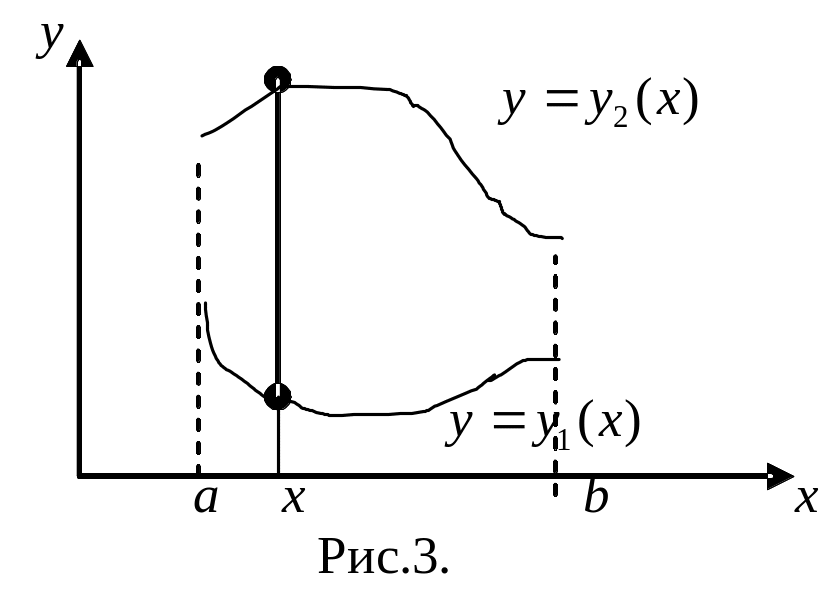 Область, в которой
всякая прямая параллельная оси
Область, в которой
всякая прямая параллельная оси![]() ,
проходящая через внутреннюю точку
области, пересекает ее границы в двух
точках, называется правильной
относительно
оси
(рис.3).
,
проходящая через внутреннюю точку
области, пересекает ее границы в двух
точках, называется правильной
относительно
оси
(рис.3).
Аналогично
определяется о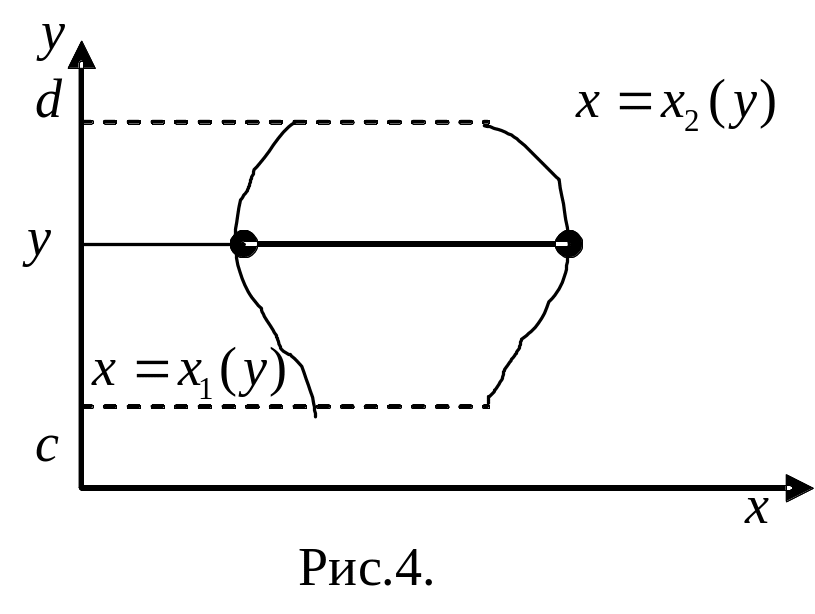 бласть
правильная
относительно оси
бласть
правильная
относительно оси![]() :
:
![]() где
функции
где
функции
![]() и
и
![]() -
непрерывные функции на отрезке
-
непрерывные функции на отрезке
![]() (рис.4).
(рис.4).
Выражения вида
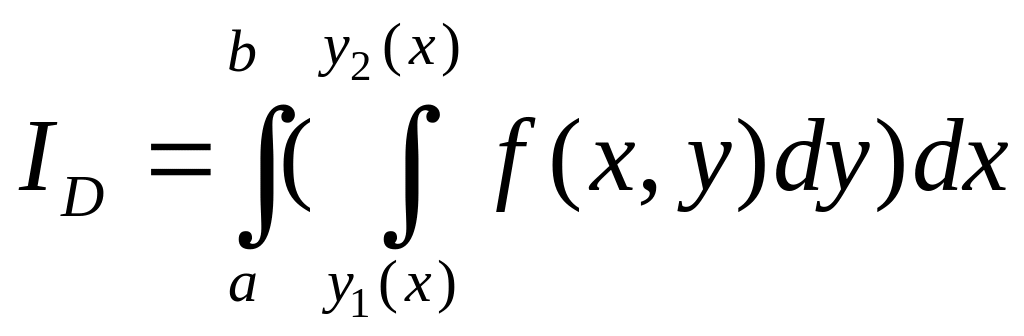 ,
,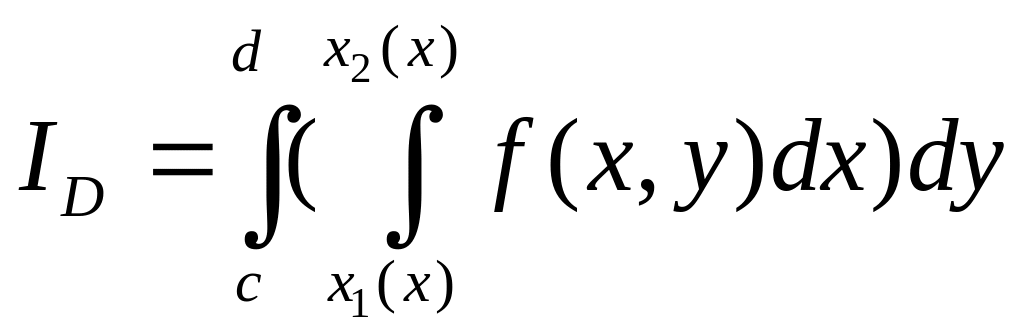
называются повторными интегралами от функции по
области .
Теорема. Двойной интеграл от непрерывной функции по правильной области равен повторному интегралу от этой функции по области .
![]()
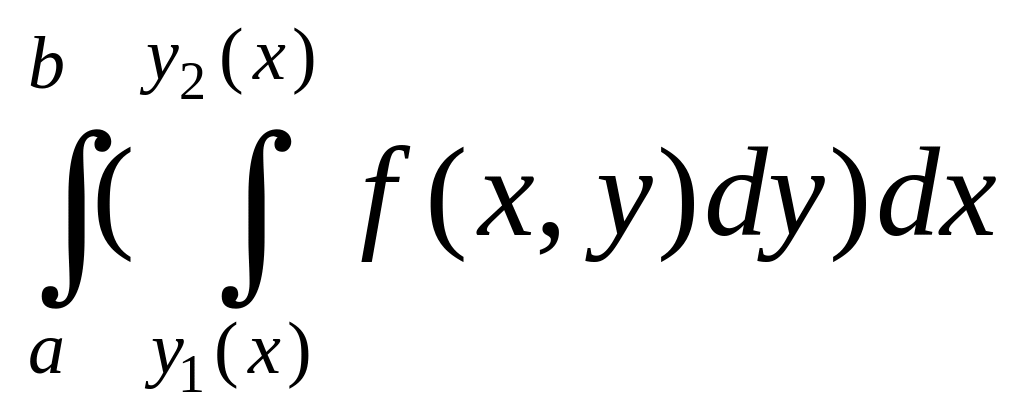 =
= .
.
Если область правильная относительно оси , то двойной интеграл вычисляется как повторный вида
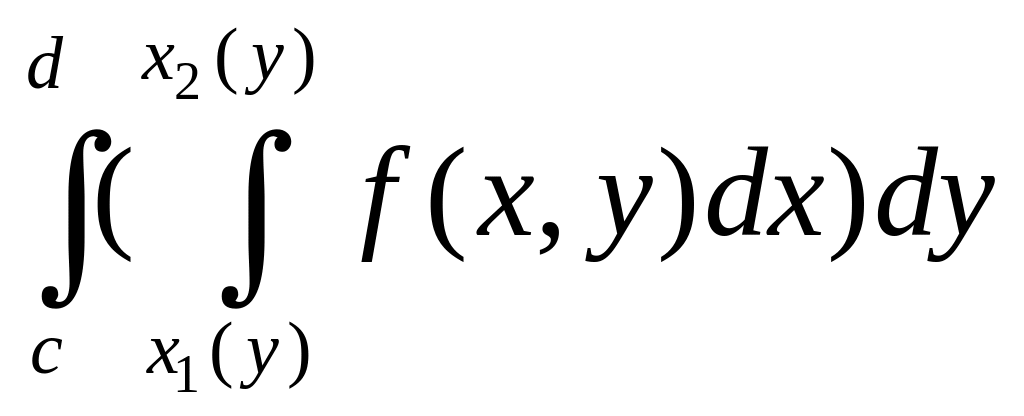 =
=
В случае, когда область не является правильной, ее разбивают на части, каждая из которых является правильной.
Частный
случай. Если
область интегрирования есть прямоугольник,
ограниченный прямыми
![]()
![]() то
формула преобразования двойного
интеграла в повторный имеет вид
то
формула преобразования двойного
интеграла в повторный имеет вид
![]() .
.
Если
кроме того, в подынтегральной функции
переменные разделены, то есть![]() ,
то двойной интеграл превращается в
произведение двух определенных
интегралов:
,
то двойной интеграл превращается в
произведение двух определенных
интегралов:
![]()
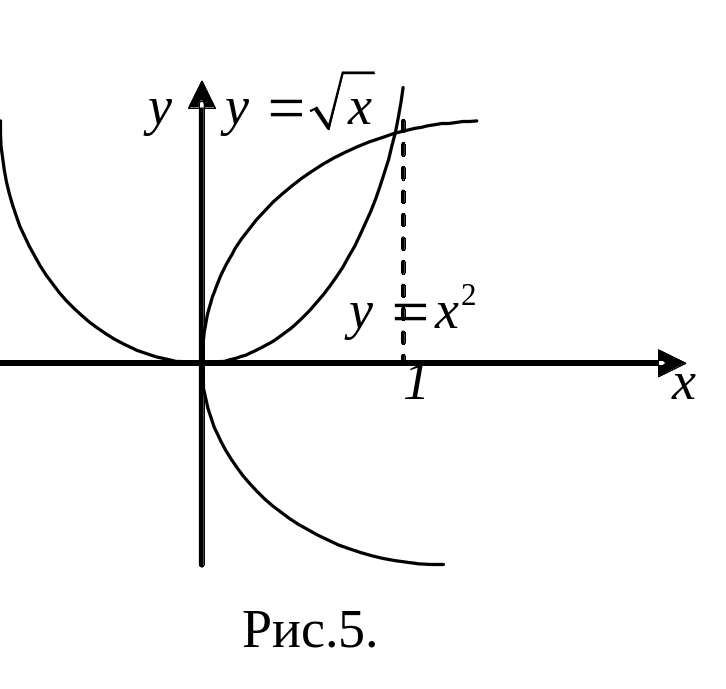
![]() .
.
Пример.
Найти![]() ,
где
-
область, ограниченная линиями
,
где
-
область, ограниченная линиями
![]() (рис.5).
(рис.5).
Решение. =
=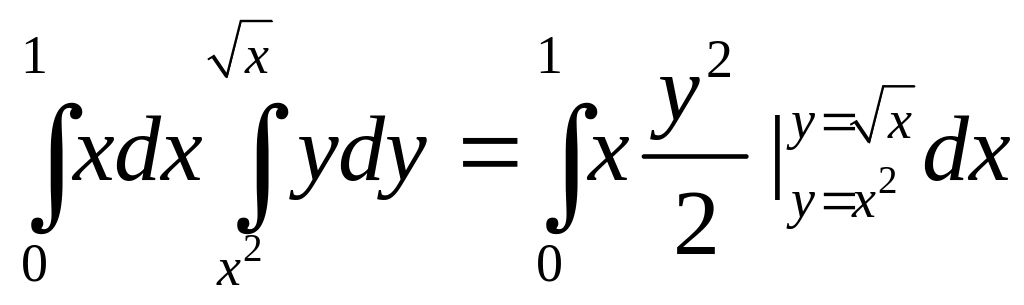
![]()
Пример.
Найти![]() ,
где
-
квадрат
,
где
-
квадрат
![]() (рис.6).
(рис.6).
 Решение.
=
Решение.
=
=
![]()
![]()
Представление двойного интеграла в виде повторного
=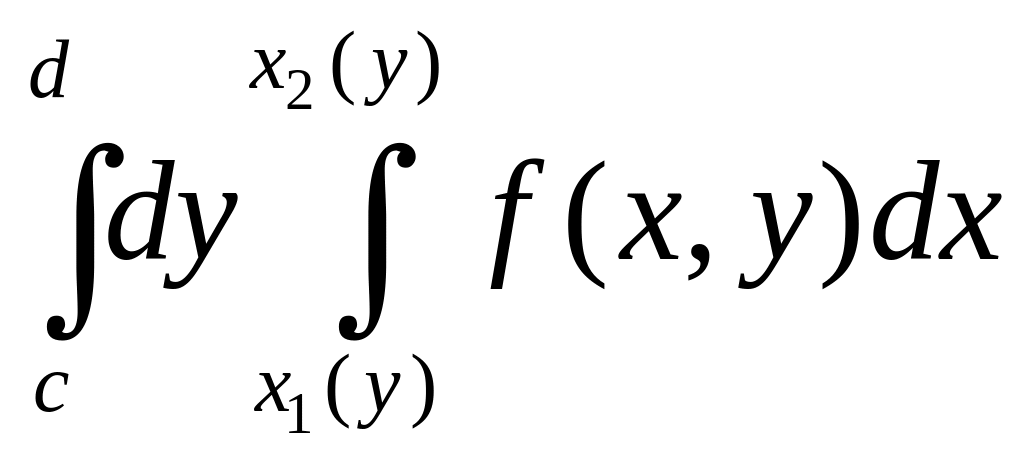
называют расстановкой пределов интегрирования в определенном порядке. Задача расстановки пределов интегрирования допускает несколько вариантов.
1. Задан двойной интеграл по области . Расставить пределы интегрирования в том и другом порядке.
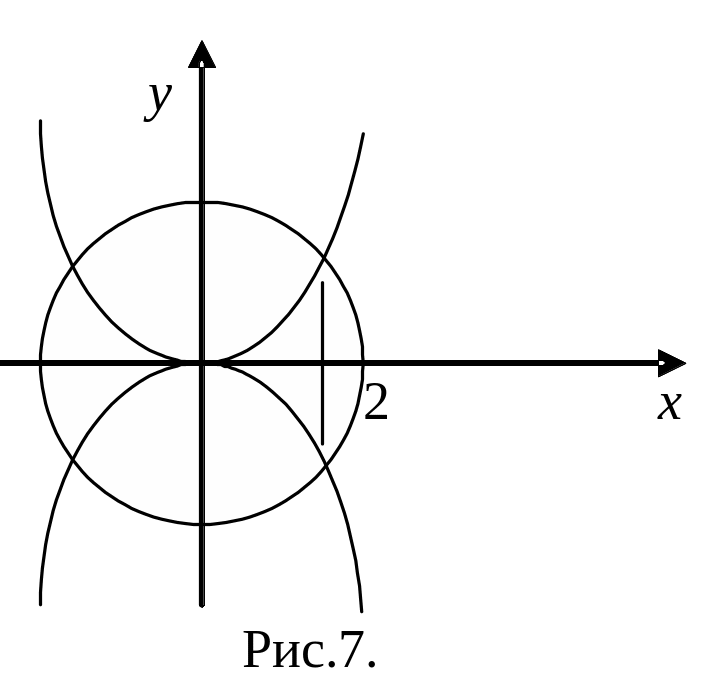 Пример. Область
лежит в правой полуплоскости (т.е.
Пример. Область
лежит в правой полуплоскости (т.е.
![]() и
ограничена
и
ограничена
кривыми:
![]() (рис.7). В двойном интеграле
расставить пределы интегрирования в
одном и другом порядке.
(рис.7). В двойном интеграле
расставить пределы интегрирования в
одном и другом порядке.
Решение. Запишем неравенства, которым должны удовлетворять координаты точек области :
![]()
![]() или
или
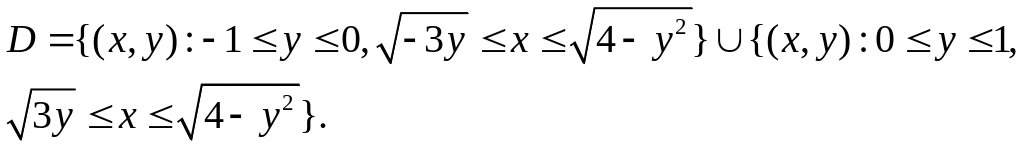
Расставим пределы интегрирования
=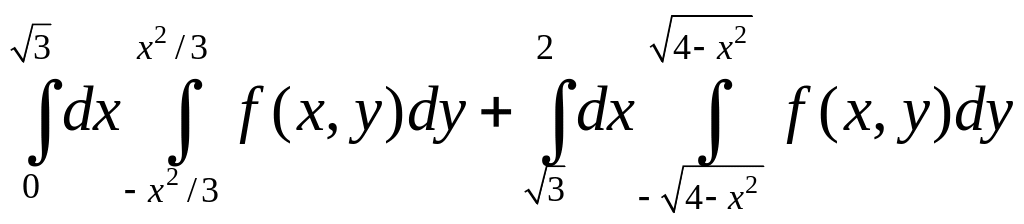 =
=

2. Задан двойной интеграл по области . Расставить пределы интегрирования в каком-либо порядке.
В этом случае выбирают порядок интегрирования, при котором интеграл имеет наиболее простое представление. Выбор может определяться как видом области интегрирования, так и свойствами подынтегральной функции. Например, расстановка пределов в одном порядке требует разбиения множества на меньшее число составляющих, чем расстановка в другом порядке.
 Пример. Расставить
пределы интегрирования в интеграле
,
где
-
область ограниченная линиями:
Пример. Расставить
пределы интегрирования в интеграле
,
где
-
область ограниченная линиями:![]() ,
,
![]() ,
,![]() (рис.8).
(рис.8).
Решение.
Для расстановки пределов интегрирования
в порядке
![]() можно не разбивать
на составляющие области, а для другого
порядка расстановки пределов такое
разбиение необходимо. Исходя из этого
выбираем порядок
.
Решая систему
можно не разбивать
на составляющие области, а для другого
порядка расстановки пределов такое
разбиение необходимо. Исходя из этого
выбираем порядок
.
Решая систему
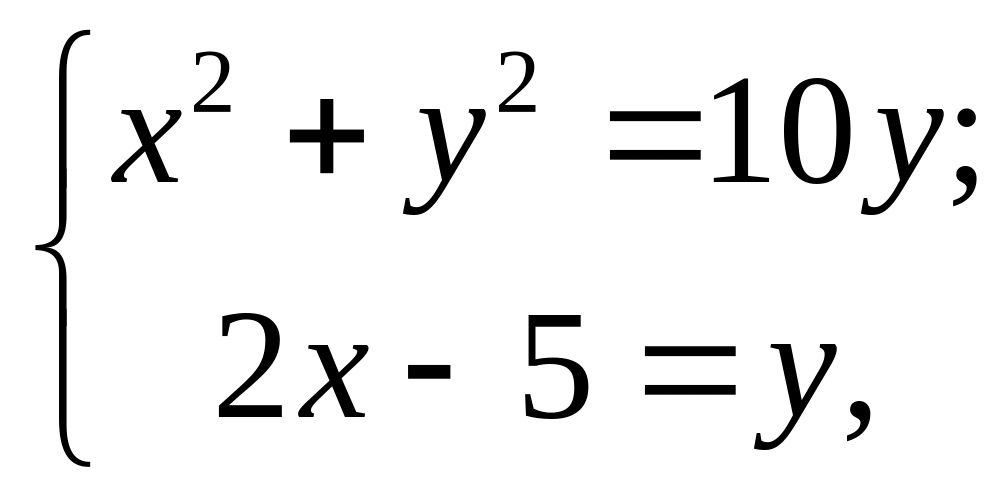 получаем координаты точек пересечения:
получаем координаты точек пересечения:![]() .
Следовательно,
.
Следовательно,
![]() и
=
и
=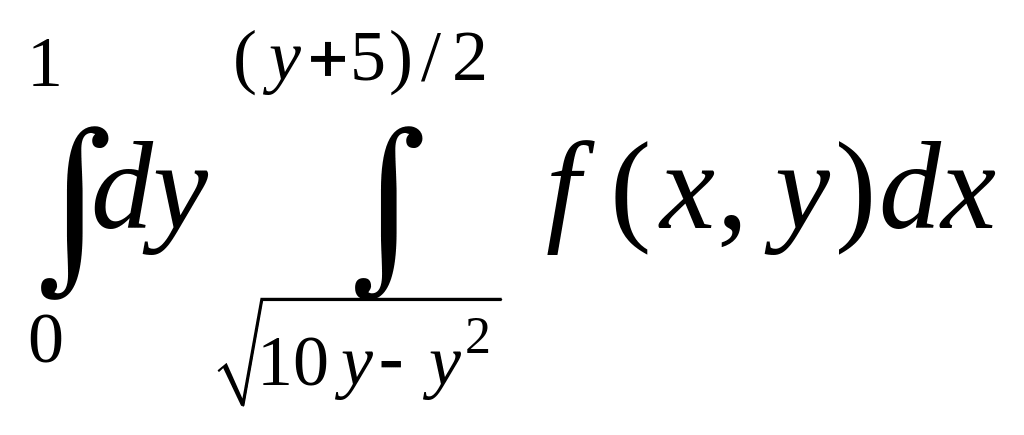 .
.
3.Задан повторный интеграл . Поменять порядок интегрирования.
Для
решения такой задачи сначала делают
переход от заданного повторного интеграла
к двойному, то есть восстанавливают по
данным пределам область интегрирования
:
=
.
Условия на координаты точек (![]() множества
получаем исходя из заданного повторного
интеграла
множества
получаем исходя из заданного повторного
интеграла
![]()
![]() .
В полученном двойном интеграле проведем
расстановку пределов интегрирования
в требуемом порядке. Таким образом,
считая область
правильной относительно обеих осей
и
,
получаем цепочку равенств
.
В полученном двойном интеграле проведем
расстановку пределов интегрирования
в требуемом порядке. Таким образом,
считая область
правильной относительно обеих осей
и
,
получаем цепочку равенств
= = .
 Пример. Изменить
порядок интегрирования в повторном
интеграле
Пример. Изменить
порядок интегрирования в повторном
интеграле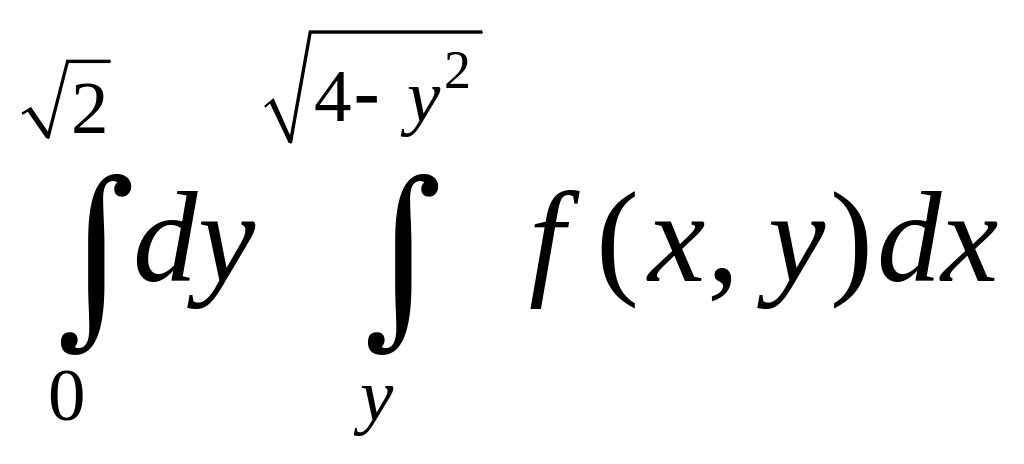 .
.
Решение.
Запишем условие на координаты точек
![]() из множества
,
по которому берется
из множества
,
по которому берется
интеграл:
![]() (рис.9).
(рис.9).
Область
правильная как относительно оси
,
так и относительно оси
.
Так как при интегрировании в порядке
![]() верхняя граница области
задается двумя различными функциями,
представим множество
в виде
верхняя граница области
задается двумя различными функциями,
представим множество
в виде![]() ,
где
,
где

Итак,
= .
.
Двойной интеграл в полярной системе координат
Выведем формулу перехода от декартовых координат к полярным в двойном интеграле.
 Пусть
- непрерывная функция на ограниченной
замкнутой области
.
Так как при определении двойного
интеграла предел последовательности
интегральных сумм не зависел от способа
разбиения области
на
части
,
то разобьем область
на
концентрическими окружностями
Пусть
- непрерывная функция на ограниченной
замкнутой области
.
Так как при определении двойного
интеграла предел последовательности
интегральных сумм не зависел от способа
разбиения области
на
части
,
то разобьем область
на
концентрическими окружностями
![]() и лучами
и лучами
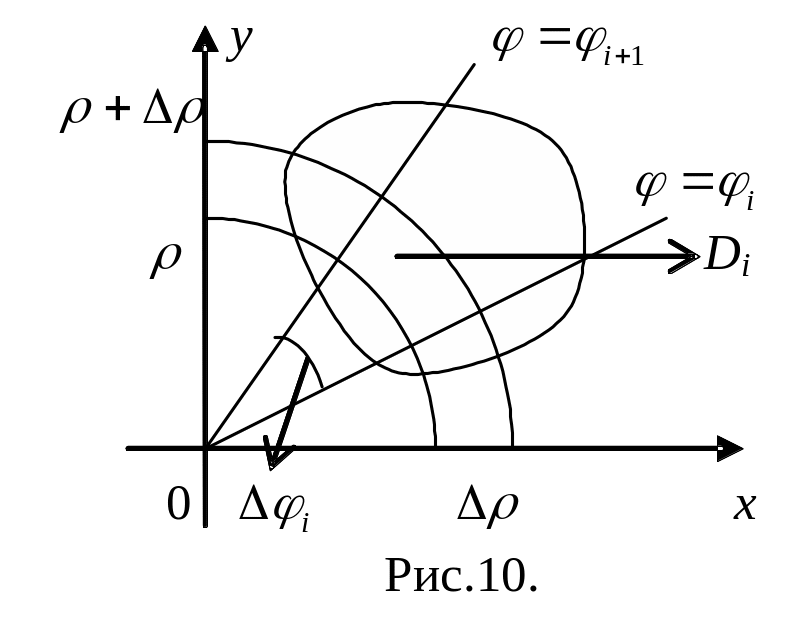
![]() (рис.10). Тогда площадь
(рис.10). Тогда площадь
![]()
с
точностью до бесконечно малых более
высокого порядка малости чем
![]() .
Таким образом, двумерный элемент
площади в полярных координатах
запишется в виде
.
Таким образом, двумерный элемент
площади в полярных координатах
запишется в виде
![]() .
.
 Пусть теперь
область
правильная относительно
Пусть теперь
область
правильная относительно![]() ,
то есть любой луч, исходящий из полюса
и проходящий через внутреннюю точку
области пересекает границу области
только в двух точках. В этом случае
область
можно задать множеством
,
то есть любой луч, исходящий из полюса
и проходящий через внутреннюю точку
области пересекает границу области
только в двух точках. В этом случае
область
можно задать множеством
![]() (рис.11).
Тогда повторный интеграл по области
представим в виде
(рис.11).
Тогда повторный интеграл по области
представим в виде

Е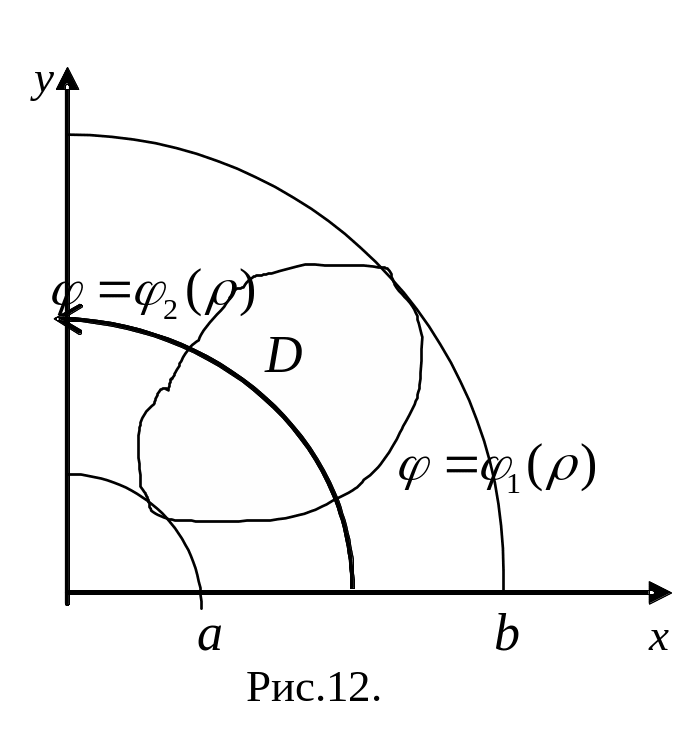 сли
любая окружность с центром в начале
координат, проходящая через внутреннюю
точку области пересекает линию границы
в двух точках, то есть область
есть множество:
сли
любая окружность с центром в начале
координат, проходящая через внутреннюю
точку области пересекает линию границы
в двух точках, то есть область
есть множество:
![]()
 ,
(рис.12), то повторный интеграл примет
вид
,
(рис.12), то повторный интеграл примет
вид
![]()
=
В случае, когда полюс лежит внутри области и любой луч пересекает границу не более чем в одной точке (рис.13), для вычисления удобно использовать формулу

Пример.
Вычислить двойной интеграл
![]() в
в
полярной
системе координат по области
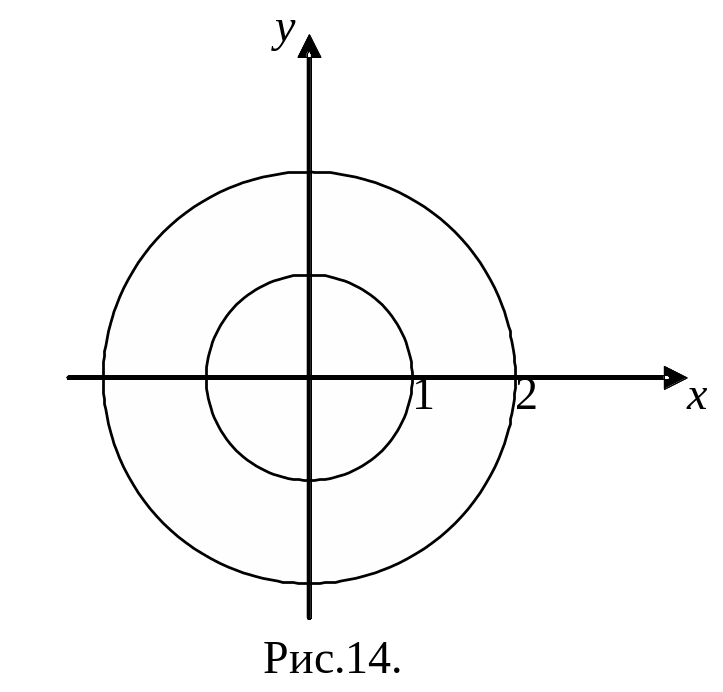
,
ограниченной линиями![]() ,
расположенной в I
квадранте (рис.14).
,
расположенной в I
квадранте (рис.14).
 Решение.
Решение.
![]()
![]()
![]()
 Пример. Вычислить
двойной интеграл
Пример. Вычислить
двойной интеграл
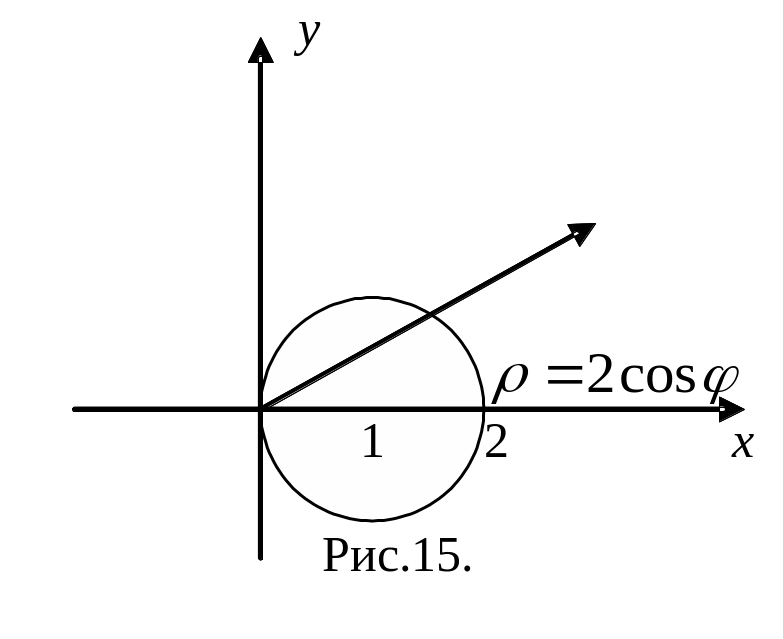
![]() в полярной системе координат по области
,
ограниченной окружностью
в полярной системе координат по области
,
ограниченной окружностью![]() (рис.15).
(рис.15).
Решение. Перейдем к полярным координатам c полюсом в точке
![]() :
:![]() Угол
Угол
![]() изменяется от
изменяется от
![]() до
до
![]() Подставляя полярные
Подставляя полярные
координаты
в уравнение окружности, получим![]() ,
откуда
,
откуда
![]() или
или
![]() - уравнение окружности в полярных
координатах. Двойной интеграл по области
сводится повторному
- уравнение окружности в полярных
координатах. Двойной интеграл по области
сводится повторному
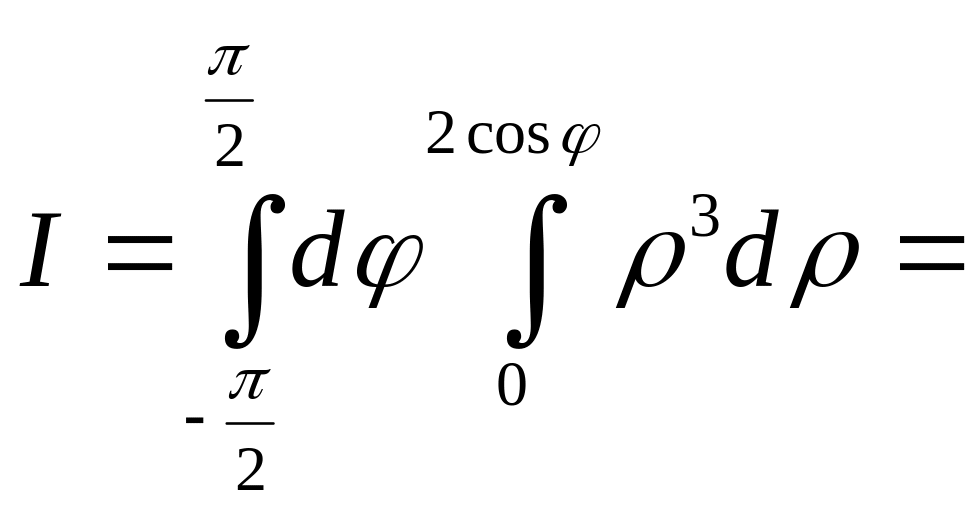

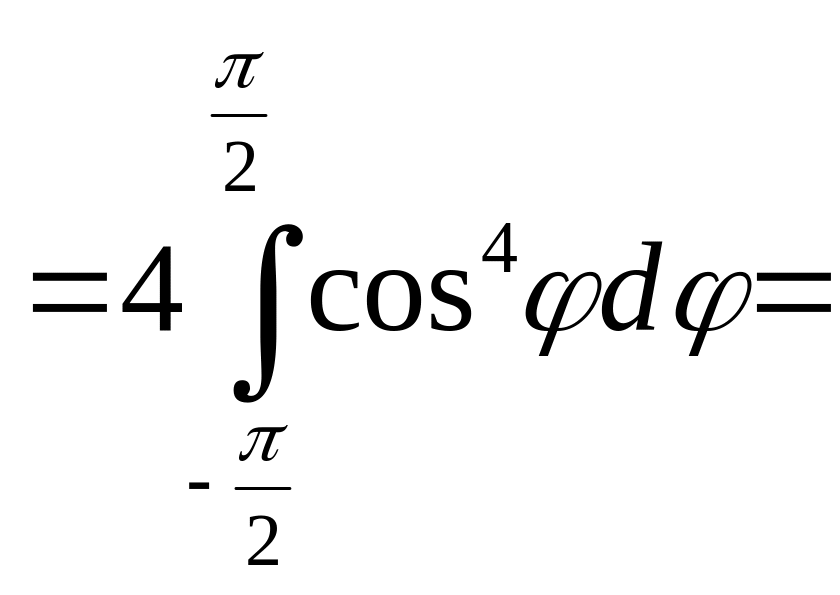
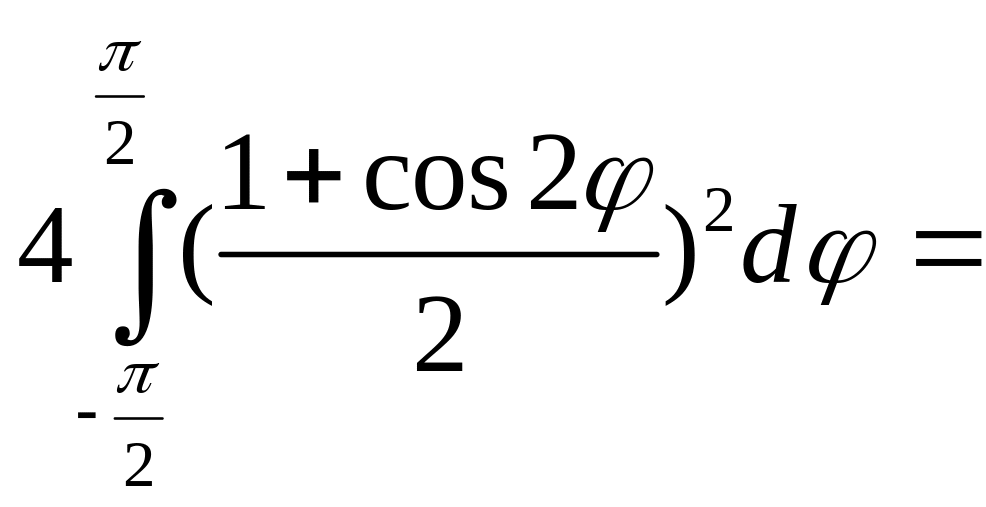
 =
=![]()
![]()
![]()
Замена переменных в двойном интеграле.
Рассмотрим двойной интеграл вида . Замена переменных в двойном интеграле состоит в переходе от
переменных
![]() и
и
![]() к новым переменным
к новым переменным
![]() и
и
![]() по формулам
по формулам
![]() ,
,![]() .
При этом каждая точка
области
соответствует некоторой точке
.
При этом каждая точка
области
соответствует некоторой точке
![]() области
области![]() ,
а каждая точка
области
переходит в некоторую точку
области
,
а каждая точка
области
переходит в некоторую точку
области
![]() Функции
называют также отображением области
плоскости
на область
плоскости
.
Пусть отображение удовлетворяет
следующим условиям:
Функции
называют также отображением области
плоскости
на область
плоскости
.
Пусть отображение удовлетворяет
следующим условиям:
1.
Отображение взаимно однозначно, то есть
различным точкам
![]() области
соответствуют различные точки
области
соответствуют различные точки
![]() области
.
области
.
2.Функции имеют в области непрерывные частные производные первого порядка.
3.
Якобиан отображения![]()
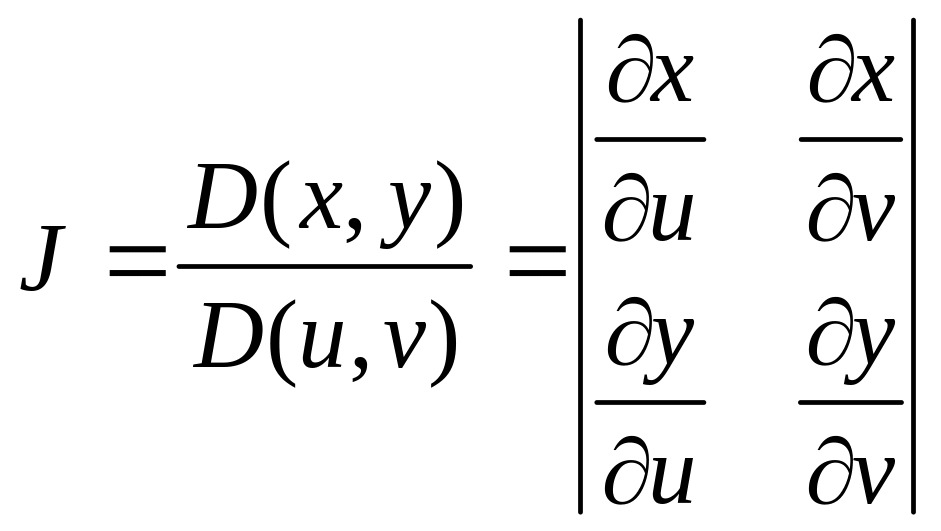 отличен от нуля во всех точках области
.
отличен от нуля во всех точках области
.
Тогда справедливо равенство
=![]()
Эта формула называется формулой замены переменных в
двойном интеграле.
Замечание. При переходе к полярной системе координат якобиан перехода имеет вид
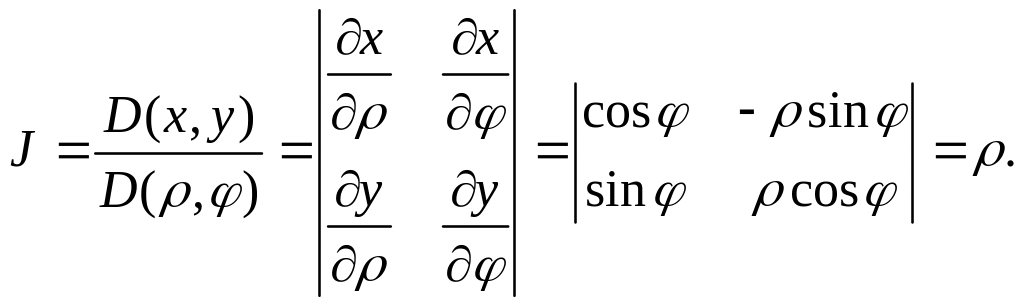
Приложения двойных интегралов.
Двойные интегралы применяются для вычисления площадей плоских фигур и поверхностей, объемов пространственных тел, механических величин связанных с непрерывным распределением массы в плоской области, а также для решения многих других задач.
