
- •II начало термодинамики. Тепловые двигатели
- •Предисловие
- •1. Теоретическая часть
- •Состояние термодинамической системы. Процесс
- •1.2. Принцип действия тепловой и холодильной машин
- •1.3. Цикл Карно
- •1.4. Второе начало термодинамики.
- •1.5. Технические циклы
- •Примеры решения задач на расчет кпд тепловых двигатлей
- •Задача 2.11. Исходя из 2 начала термодинамики, выраженного в виде , вычислить кпд цикла Карно. (рис. 2.11)
- •3. Задачи для самостоятельного решения по теме «тепловые двигатели»
- •II начало термодинамики. Тепловые двигатели
- •394026 Воронеж, Московский просп., 14
Примеры решения задач на расчет кпд тепловых двигатлей
Задача 2.1. Идеальный двухатомный
газ, содержащий количество вещества
![]() ,
находится под давлением
,
находится под давлением
![]() -
и занимает объем
-
и занимает объем
![]() .
Сначала газ изохорно нагревают до
температуры
.
Сначала газ изохорно нагревают до
температуры
![]() .
Далее, изотермически расширяя, доводят
его до первоначального давления. После
этого путем изобарного сжатия возвращают
газ в начальное состояние. Определит
термический КПД
цикла.
.
Далее, изотермически расширяя, доводят
его до первоначального давления. После
этого путем изобарного сжатия возвращают
газ в начальное состояние. Определит
термический КПД
цикла.
Дано:
|
|
Д
Рис. 2.1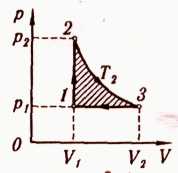
Термический КПД любого цикла определяется
выражением
![]()
или
![]() (1)
(1)
где - количество теплоты, полученное газом за цикл от нагревателя; - количество теплоты, отданное газом за цикл охладителю.
Разность количеств теплоты
![]() равна работе А, совершаемой газом за
цикл. Эта работа на графике в координатах
р,V (рис.2.1) изображается площадью цикла
(площадь цикла заштрихована).
равна работе А, совершаемой газом за
цикл. Эта работа на графике в координатах
р,V (рис.2.1) изображается площадью цикла
(площадь цикла заштрихована).
Рабочее вещество (газ) получает количество
теплоты
на двух участках:
![]() на участке 1 - 2 (изохорный процесс) и
на участке 1 - 2 (изохорный процесс) и
![]() ,
на участке 2 - 3 (изотермический процесс).
Таким образом
,
на участке 2 - 3 (изотермический процесс).
Таким образом
![]() .
.
Количество теплоты, полученное газом при изохорном процессе, равно
![]()
где
![]() - молярная теплоемкость газа при
постоянном объеме; и
- молярная теплоемкость газа при
постоянном объеме; и
![]() количество
вещества. Температуру
начального состояния газа, воспользовавшись
уравнением Клапейрона—Менделеева:
количество
вещества. Температуру
начального состояния газа, воспользовавшись
уравнением Клапейрона—Менделеева:
![]() .
.
Подставив числовые значения и произведя вычисления, получим
![]() .
.
Количество теплоты, полученное газом при изотермическом процессе, равно
![]() ,
,
где - объем, занимаемый газом при температуре и давлении (точка 3 на графике).
На участке 3 - 1 газ отдает количество теплоты , равное
![]() ,
,
где Ср — молярная теплоемкость газа при изобарном процессе.
Подставим найденные значения и в формулу (1):
![]() .
.
В полученном выражении заменим отношение
объемов
,
согласно закону Гей-Люссака, отношением
температур
![]() и выразим
и
и выразим
и
![]() через число степеней свободы молекулы
через число степеней свободы молекулы
![]() .
Тогда после сокращения на
и
.
Тогда после сокращения на
и
![]() получим
получим
![]() .
.
Подставив значения
![]() и
и
![]() ,
и произведя вычисления, найдем
,
и произведя вычисления, найдем
= 0,041 =4 ,1 %
Ответ: = 4,1 %
Задача 2.2. Температура пара,
поступающего в паровую машину,
![]() ;
температура в конденсаторе
;
температура в конденсаторе
![]() .
Определить теоретически максимальную
работу при затрате количества теплоты
.
Определить теоретически максимальную
работу при затрате количества теплоты
![]() .
.
Дано:
|
|
Д
Рис. 2.2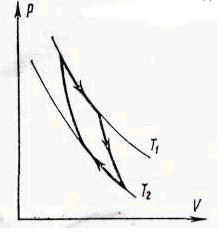 ля
того чтобы работа, совершаемая тепловой
машиной (тепловым двигателем), была
максимальной, необходимо, чтобы цикл,
по которому работает двигатель, был
обратимым. При наличии только двух
термостатов - нагревателя с температурой
ля
того чтобы работа, совершаемая тепловой
машиной (тепловым двигателем), была
максимальной, необходимо, чтобы цикл,
по которому работает двигатель, был
обратимым. При наличии только двух
термостатов - нагревателя с температурой
![]() и холодильника с температурой
и холодильника с температурой
![]() - возможен только один обратимый цикл
- цикл Карно, состоящий из двух изотерм
и двух адиабат (рис.2.2.).
- возможен только один обратимый цикл
- цикл Карно, состоящий из двух изотерм
и двух адиабат (рис.2.2.).
Коэффициент полезно действия этого цикла
![]() (1)
(1)
КПД любого теплового двигателя
![]() ,
(2)
,
(2)
где А - полезная работа, совершаемая двигателем, - количество теплоты, полученное рабочим телом от нагревателя.
Приравнивая правые части равенств (I) и (2), получим
![]() ,
,
откуда
![]() .
.
Ответ: А=1,05 кДж.
Задача 2.3. Тепловой двигатель работает по циклу, состоящему из изотермического, изобарного и адиабатного процессов. При изобарном процессе рабочее тело - идеальный газ - нагревается от температуры Т1 = 200 К до Т2 = 500 К. Определить коэффициент полезного действия данного теплового двигателя и двигателя, работающего по циклу Карно, происходящему между максимальной и минимальной температурами данного цикла.
Дано:
|
|
В условии задачи неоговорена
последовательность процессов, но
поскольку изобарный процесс, по условию,
- процесс нагревания, следовательно, и
расширения, а тепловая машина является
тепловым двигателем, то прямая,
соответствующая графику этого процесса
в координатах р,V, должна лежать выше
кривых, изображающих изотермический и
адиабатный процессы. После изобарного
расширения 1- 2 (рис. 2.3) газ должен а
Рис. 2.3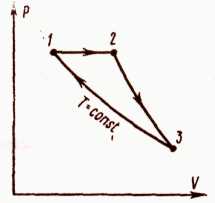 диабатно
расширяться (кривая 2-3) до тех пор, пока
температура станет равной
,
а затем изотермическим сжатием (кривая
3-1) газ можно вернуть в исходное состояние.
(Легко убедиться, что при любой другой
последовательности процессов не будет
выполняться условие з
диабатно
расширяться (кривая 2-3) до тех пор, пока
температура станет равной
,
а затем изотермическим сжатием (кривая
3-1) газ можно вернуть в исходное состояние.
(Легко убедиться, что при любой другой
последовательности процессов не будет
выполняться условие з
При последовательности процессов,
изображенной на рис. 2.3 газ получает
теплоту только в процессе 1-2, поэтому
![]() ,
и отдает теплоту в процессе 3-1 (
,
и отдает теплоту в процессе 3-1 (![]() ).
Процесс 2-3 происходит без теплообмена.
Тогда коэффициент полезного действия
цикла, согласно определению,
).
Процесс 2-3 происходит без теплообмена.
Тогда коэффициент полезного действия
цикла, согласно определению,
![]() .
(1)
.
(1)
Газ идеальный, все процессы предполагаются
обратимыми (фактически это предположение
было сделано уже при изображении
процессов на графике). Тогда
и
![]() могут быть выражены по известным формулам
для изобарного и изотермического
процессов.
могут быть выражены по известным формулам
для изобарного и изотермического
процессов.
Коэффициент полезного действия цикла
Карно найдем по известным формулам, так
как из проведенного анализа очевидно,
что
![]() .
.
Количество теплоты, получаемое рабочим телом при изобарном процессе,
![]() ,
(2)
,
(2)
где
![]() - молярная теплоемкость при постоянном
давлении.
- молярная теплоемкость при постоянном
давлении.
Количество теплоты, отдаваемое рабочим телом при изотермическом сжатии,
![]() ,
(3)
,
(3)
Для процесса 3-1 количество теплоты
пропорционально
![]() .
Поскольку
.
Поскольку
![]() ,
логарифм будет отрицательным, поэтому
в выражении для
,
логарифм будет отрицательным, поэтому
в выражении для
![]() стоит
стоит
![]() .
.
Объемы газа и их отношения неизвестны, однако состояния I и 2 лежат на одной изобаре и
![]() .
(4)
.
(4)
Состояния 2 и 3 лежат на одной адиабате:
![]() .
(5)
.
(5)
Учитывая, что
![]() ,
и извлекая корень степени
,
и извлекая корень степени
![]() ,
получаем
,
получаем
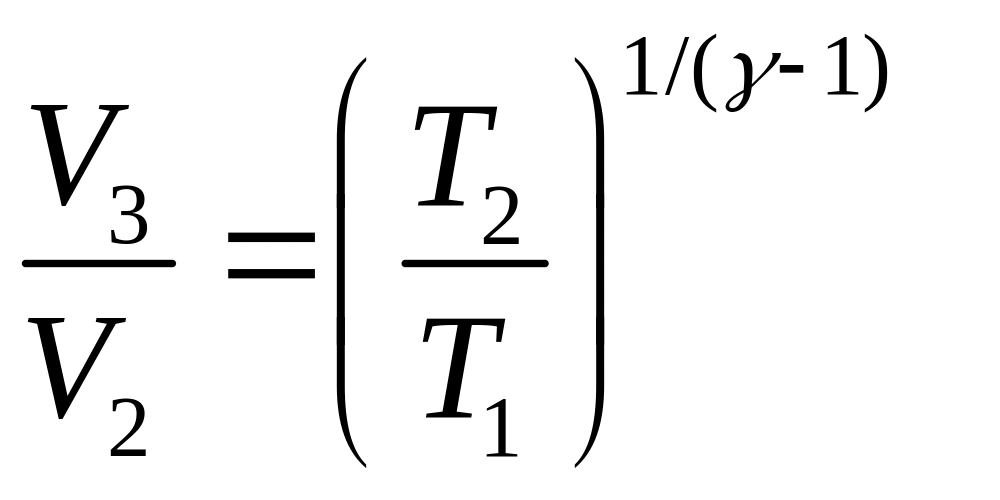 (6)
(6)
Перемножая почленно равенства (4) и (6), имеем
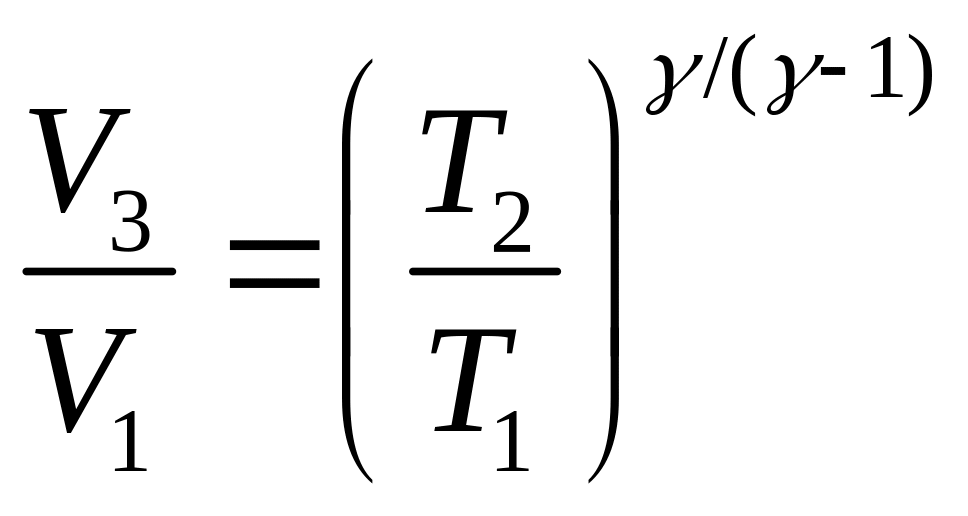 .
.
Тогда
![]() .
.
![]() .
(7)
.
(7)
Подставим выражения (2) и (7) в (1):
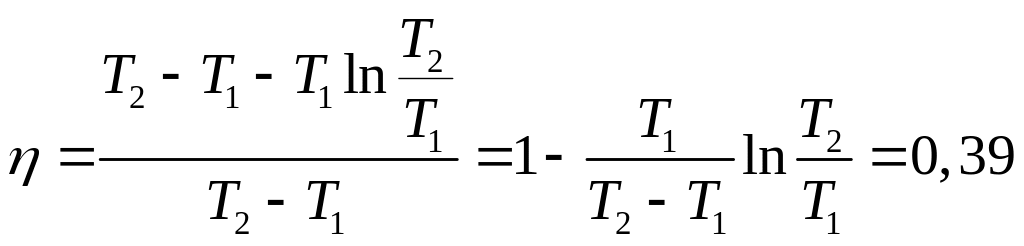 .
.
Коэффициент полезного действия цикла Карно между максимальной и минимальной температурами
![]()
Ответ: =0,39
Задача 2.4. В цикле Отто газовых и карбюраторных двигателей внутреннего сгорания теплота подводится и отводится при постоянных объемах (рис. 2.4). Особенностью таких двигателей является то, что в них сжимается рабочая смесь, приготовленная вне цилиндров:
0—1 - всасывание рабочей смеси (горячий газ - воздух либо пары легкого топлива - воздух);
/—2 - адиабатическое сжатие рабочей смеси.
В конце сжатия происходит зажигание горючей смеси от электрической искры;
2—3 - быстрое возрастание давления продуктов сгорания (практически при постоянном объеме) и их температуры;
3—4 - адиабатическое расширение продуктов сгорания (рабочий ход поршня). В конце расширения открывается выпускной клапан, происходит падение давления в цилиндре (ветвь 4-1) при постоянном объеме;
1—0 - выталкивание поршнем продуктов сгорания.
О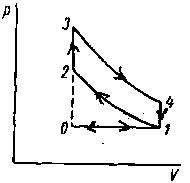 тношение
тношение
![]()
называется степенью адиабатического сжатия.
Рис. 2.4
Дано:
|
|
КПД цикла
![]() (1)
(1)
Подводимая теплота соответствует ветви
2-3 (![]() ),
тогда
),
тогда
![]() ,
(2)
,
(2)
где - число молей, - молярная теплоемкость рабочей смеси.
Аналогично
![]() .
(3)
.
(3)
Тогда разделив (3) на (2), получим
![]() (4)
(4)
Так как ветви 3-4 и 1-2 – адиабаты, то
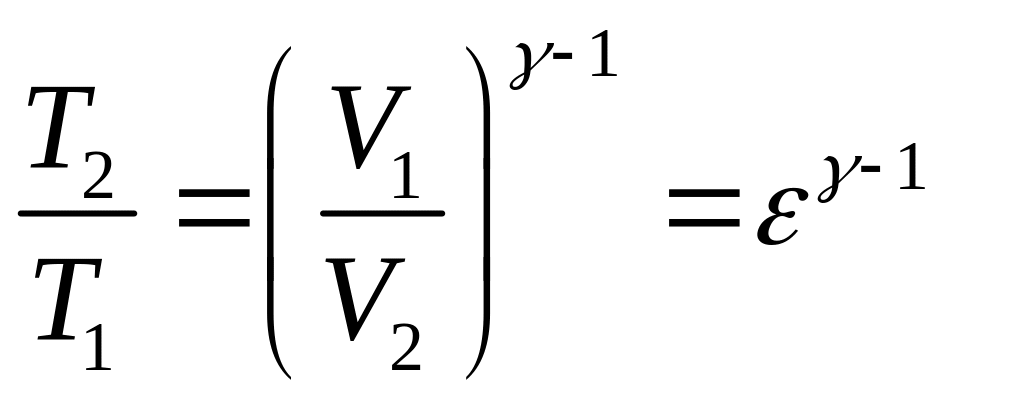 (5)
(5)
и
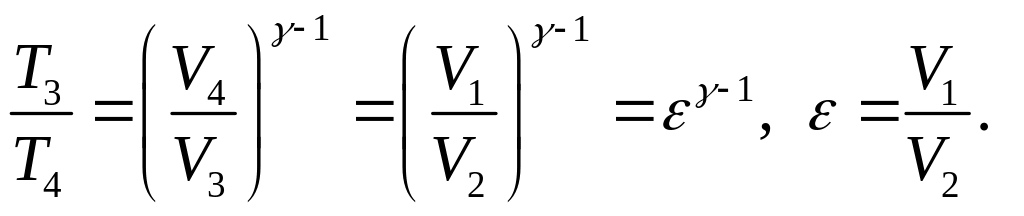
![]() (6)
(6)
Из (5) и (6), следует, что
![]() (7)
(7)
![]() (8)
(8)
Подставив (7) и (8) в (4), получим сначала
![]() (9)
(9)
а затем выражение для КПД цикла
![]() (10)
(10)
Ответ:
![]()
Задача 2.5. Карбюраторный двигатель
внутреннего сгорания работает по циклу,
состоящему из двух адиабат и двух изохор.
Рассчитать КПД двигателя при следующих
значениях температур:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Дано:
|
|
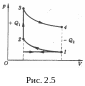
![]()
где
![]()
![]()
![]()
Ответ: = 0,38.
Задача 2.6. Цикл четырехтактного
двигателя Дизеля изображен на рисунке
2.6 а) ветвь АВ – в цилиндры засасывается
воздух(Р0=1ат) б) ветвь ВС – воздух
адиабатически сжимается д о
давления Р1 в) в конце такта
сжатия в цилиндры впрыскивается топливо,
которое воспламеняется в горячем воздухе
и сгорает, при этом поршень движется
вправо сначала изобарически (ветвь
CD), а затем адиабатически
(ветвь DE). г) в конце
адиабатического расширения открывается
выпускной клапан, давление падает до
Р0 (ветвь EB). д) при
движении поршня влево смесь удаляется
из цилиндров (ветвь ВА). Найти КПД
двигателя Дизеля.
о
давления Р1 в) в конце такта
сжатия в цилиндры впрыскивается топливо,
которое воспламеняется в горячем воздухе
и сгорает, при этом поршень движется
вправо сначала изобарически (ветвь
CD), а затем адиабатически
(ветвь DE). г) в конце
адиабатического расширения открывается
выпускной клапан, давление падает до
Р0 (ветвь EB). д) при
движении поршня влево смесь удаляется
из цилиндров (ветвь ВА). Найти КПД
двигателя Дизеля.
Дано: T0, T1, T2, T3 |
|
Работа, совершаемая при полном цикле:
A=Q1-Q2 (1)
где Q1 – количество тепла, выделившееся при сгорании топлива, Q2 – количество теплоты, отданное среде (на ЕВ). Т.к. CD – изобара, то:
![]() (2)
(2)
где Т1 – температура в начале изобар. расширения, а Т2 – в конце.
Т.к. ЕВ – изохора, то:
![]() (3)
(3)
где Т3 – температура в начале изохор. процесса, а Т0 – в конце.
Следовательно:
![]() (4)
(4)
Выразим Ср через Cv
![]() (5)
(5)
Подставив (5) в (4) получим:
![]() (6)
(6)
Для КПД имеем:
![]() (7)
(7)
Ответ:
![]()
З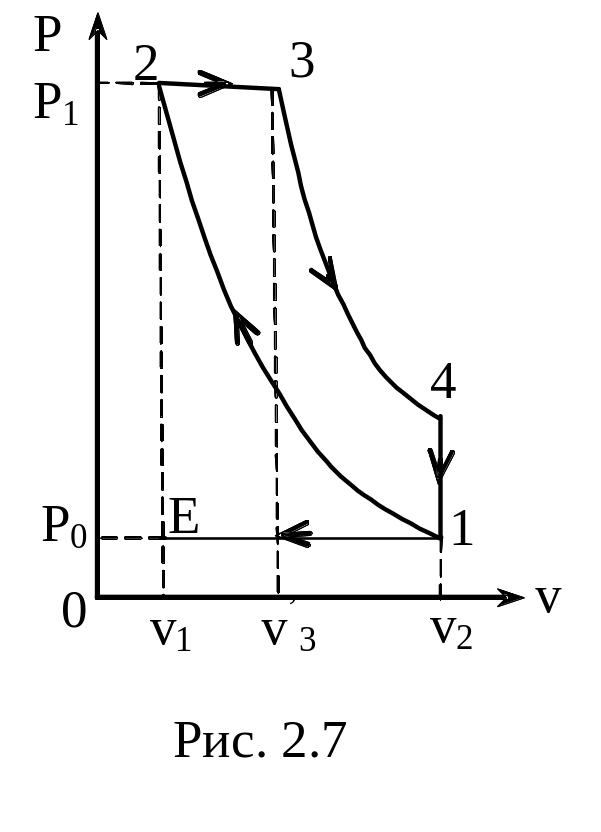 адача
2.7. Дизельный двигатель внутреннего
сгорания работает по циклу, состоящему
из 2 адиабат, изобары и изохоры (рис 2.7).
Рассчитать КПД такого двигателя, если
отношение удельных теплоемкостей
адача
2.7. Дизельный двигатель внутреннего
сгорания работает по циклу, состоящему
из 2 адиабат, изобары и изохоры (рис 2.7).
Рассчитать КПД такого двигателя, если
отношение удельных теплоемкостей
![]() , а температуры газа имеют значения:
T1=310 K,
T2=760 K,
T3=1210K,
T4=610K.
, а температуры газа имеют значения:
T1=310 K,
T2=760 K,
T3=1210K,
T4=610K.
Дано: T1=310 K T2=760 K T3=1210 K T4=610 K |
|
1-2 адиабатный процесс Q12=0
2-3 изобарный процесс
![]()
3-4 адиабатный процесс Q34=0
4-1 изохорный процесс![]()
![]() ,
,
тогда
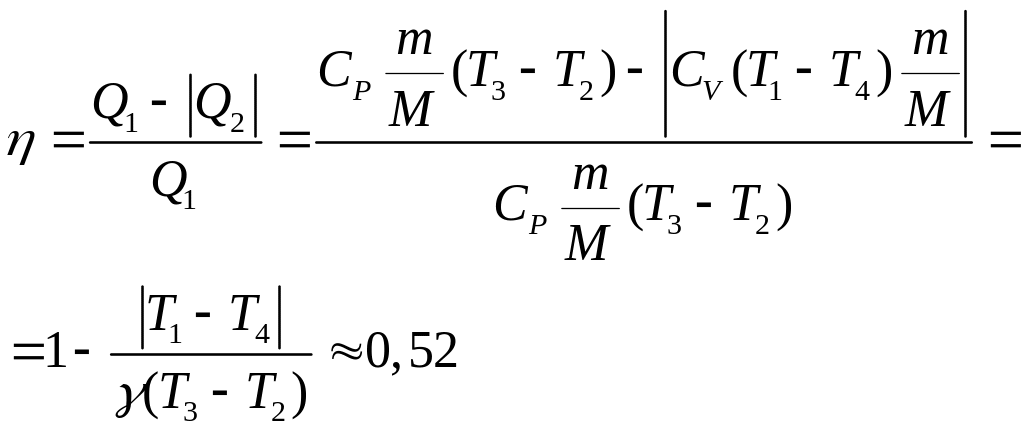
Ответ: = 0,52
Задача 2.8. Цикл газотурбинной
установки при постоянном давлении (рис
2.8) состоит: из адиабаты 1-2 (сжатие воздуха
в компрессоре перед подачей его в камеру
сгорания), адиабаты 3-4 (расширение
продуктов сгорания в соплах турб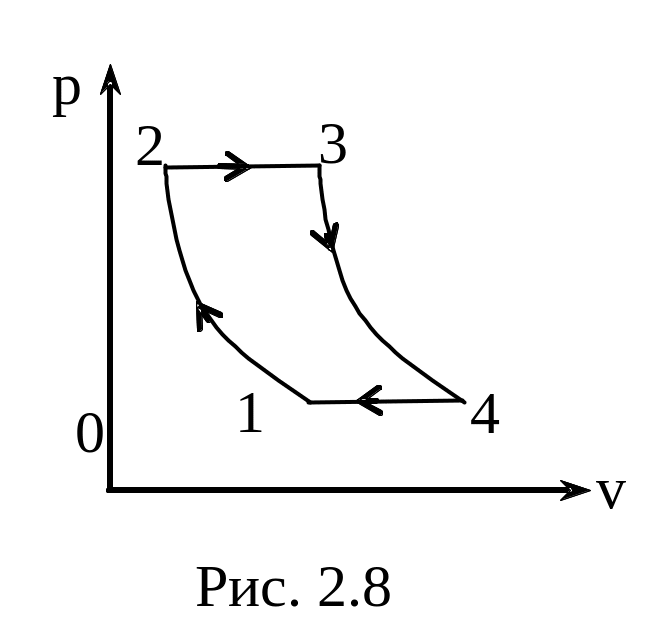 ины,
при этом совершается работа вращения
ротора) и изобары 4-1 (охлаждение
отработанных газов при атмосферном
давлении до температуры окружающей
среды). Отношение
ины,
при этом совершается работа вращения
ротора) и изобары 4-1 (охлаждение
отработанных газов при атмосферном
давлении до температуры окружающей
среды). Отношение
![]() называется степенью повышения давления.
Найти выражение для КПД цикла установки
с подводимой теплотой при Р=const.
Показатель адиабаты равен
,
теплоемкости СР воздуха и продуктов
сгорания считать равными и постоянными.
называется степенью повышения давления.
Найти выражение для КПД цикла установки
с подводимой теплотой при Р=const.
Показатель адиабаты равен
,
теплоемкости СР воздуха и продуктов
сгорания считать равными и постоянными.
Дано:
|
|
КПД цикла:
![]() (1)
(1)
где тепло, подводимое в ходе изобарического процесса 2-3:
![]() (2)
(2)
А тепло, отводимое в ходе изобарического процесса 4-1:
![]() (3)
(3)
А т.к. 1-2 адиабата, то
![]() ,
,
откуда
![]() (4)
(4)
аналогично для адиабаты 3-4
![]() ,
,
откуда
![]() (5)
(5)
Разделив (3) на (2), получим:
![]() (6)
(6)
Подставляя (6) в (1), получим:
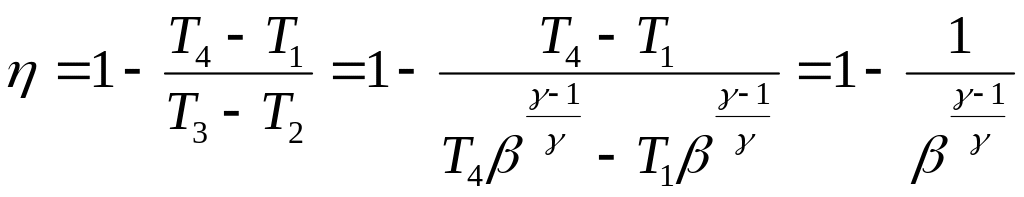 (7)
(7)
Ответ:
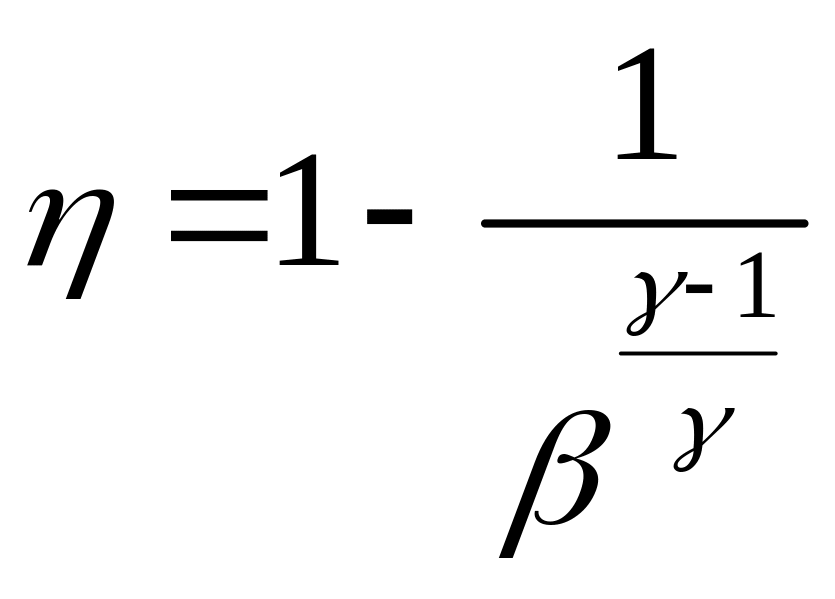
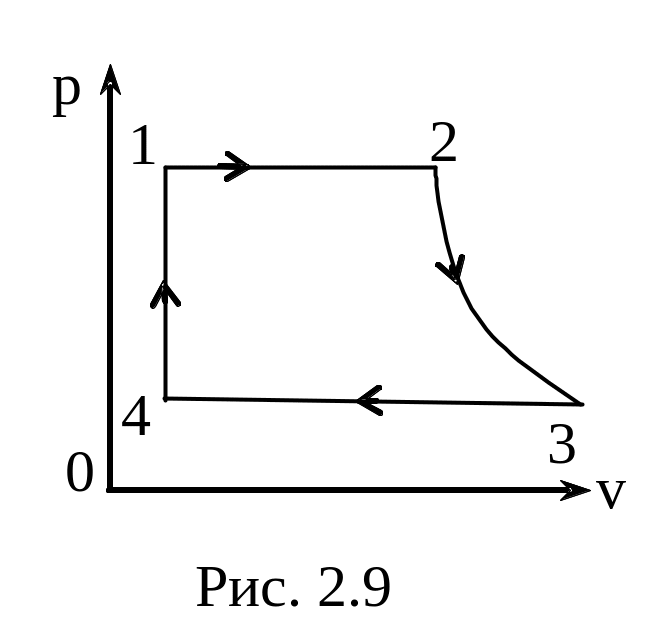
Задача 2.9. Образцовый цикл паросиловой
установки (цикл Ренкина) представлен
на рис 2.9. Нагревание воды в паровом
котле до температуры кипения, испарение
и перегревание полученного пара
происходят при постоянном давлении
(изобарное подведение теплоты происходит
по ветви 1-2). Далее следует адиабатическое
расширение пара в турбине (ветвь 2-3). В
конце расширения пар переходит линию
насыщения и увлажняется. Отработанный
пар сжимается в конденсаторе (изобарное
отведение теплоты, ветвь 3-4), а полученный
конденсат насосом снова подается в
котел (ветвь 4-1). Рассчитать приращение
энтропии при 1) нагревании воды в котле
![]() 2) при испарении
2) при испарении
![]() 3) при перегревании пара
3) при перегревании пара
![]() до 500*С , если р1=981*104 Па,
температура перегретого пара tпп=500*С,
р3=39*102Па. Среднюю удельную
теплоемкость воды при давлении р1
принять равной Ср=4620 Дж/кг*К.
Скрытая теплота испарения воды при р=p1
равна r1=133*104
Дж/кг; при р=р3 равна r3=243*104
Дж/кг. Средняя удельная теплоемкость
перегретого пара Ср=3420 Дж/кг*К.
до 500*С , если р1=981*104 Па,
температура перегретого пара tпп=500*С,
р3=39*102Па. Среднюю удельную
теплоемкость воды при давлении р1
принять равной Ср=4620 Дж/кг*К.
Скрытая теплота испарения воды при р=p1
равна r1=133*104
Дж/кг; при р=р3 равна r3=243*104
Дж/кг. Средняя удельная теплоемкость
перегретого пара Ср=3420 Дж/кг*К.
Дано: P1=981*104 Па tпара=500*C T3=773K P3=39*102 Па Cрводы=4620 Дж/кг*к При Р=Р1 r1=133*104 Дж/кг при Р=Р3 r3=243*104 Дж/кг С’рп=3420Дж/кг*К m=1 кг |
|
Из таблиц
водяного пара определяем температуры
кипения воды при давлениях Р1
![]() t1=309,5*C,
Т1=582,5 К; Р3
t3=28,6*C,
T3=301,6 K.
t1=309,5*C,
Т1=582,5 К; Р3
t3=28,6*C,
T3=301,6 K.
Изменение энтропии:
1) при нагревании воды в котле (1)
Подставив численные значения в (1), получим:
![]() (Дж/к)
(Дж/к)
2) При испарении воды
![]() (2)
(2)
Подставив численные значения в (2), найдем
![]() (Дж/К)
(Дж/К)
3) при перегревании пара до 500*С
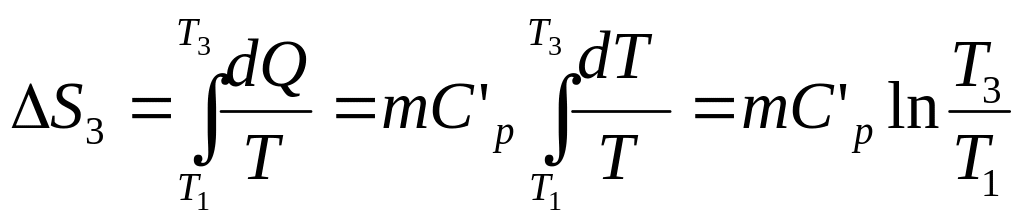 (3)
(3)
подставив численные значения в (3), получим
![]() (Дж/К)
(Дж/К)
Ответ: =3041, =2283, =968 Дж/К
Задача 2.10.
Идеальная холодильная машина работает
как тепловой насос по обратному циклу
Карно(рис. 2.10). При этом она берет тепло
от воды с температурой 2*С и передает
его воздуху с температурой 27*С. Найти
1) коэффициент
![]() - отношение количества тепла, переданного
воздуху за некоторый промежуток времени,
к количеству тепла, отнятому за это же
время у воды. 2) коэффиц
- отношение количества тепла, переданного
воздуху за некоторый промежуток времени,
к количеству тепла, отнятому за это же
время у воды. 2) коэффиц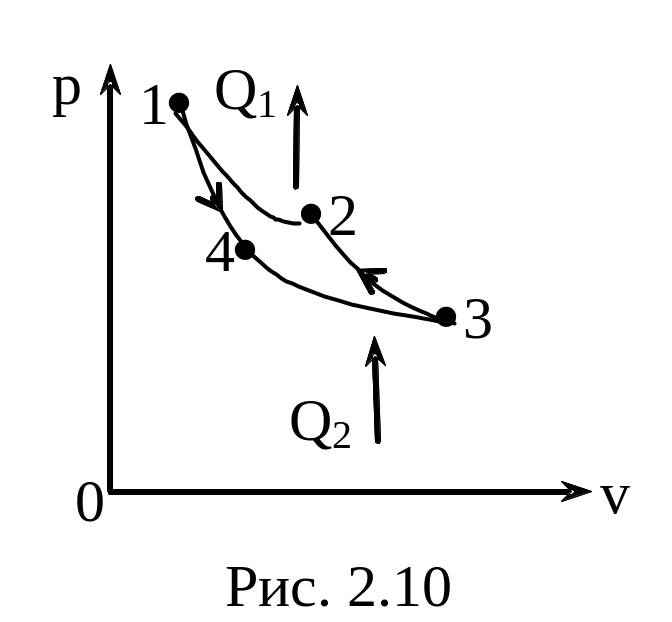 иент
иент
![]() - отношение количества тепла, отнятого
у воды, к затраченной на работу машины
энергией (
называется холодильным коэффициентом
машины), 3) коэффициент
- отношение количества тепла, отнятого
у воды, к затраченной на работу машины
энергией (
называется холодильным коэффициентом
машины), 3) коэффициент
![]() - отношение затраченной на работу машины
энергии к количеству тепла, переданному
за это время воздуху (
- КПД цикла). Найти соотношение м/у
коэффициентами
- отношение затраченной на работу машины
энергии к количеству тепла, переданному
за это время воздуху (
- КПД цикла). Найти соотношение м/у
коэффициентами
Дано: T1=300 K T2=275 K |
|
КПД прямого цикла Карно равен
![]()
В то же время
![]()
Откуда
![]()
Далее
![]() .
.
Отсюда
![]()
Тогда
![]() ;
;![]()
![]() ;
;![]()
Ответ: 1= 1,09 2= 11 3=0,083
