ФГБОУ ВПО «Воронежский государственный

технический университет »

СПРАВОЧНИК МАГНИТНОГО ДИСКА

(Кафедра высшей математики

и физико-математического моделирования)

Методические указания

к выполнению лабораторных работ дисциплины

«Математика» по направлению 110800.62 «Агроинженерия», профилю «Электроснабжение и электрооборудование сельхозпредприятий», направлению 140400.62 «Электроэнергетика и электротехника», профилям «Электромеханика», «Электропривод и автоматика» и направлению 20400.62 «Управление в технических системах», профилю «Управление и информатика в технических системах», очной формы обучения

Часть 2

Составители: А.А. Катрахова, В.С. Купцов, А.В. Купцов

Lab2. doc 6,5 Mb 14.03.2012 2,1 уч.-изд. л.

ФГБОУ ВПО «Воронежский государственный

технический университет »

Кафедра высшей математики

и физико-математического моделирования

Методические указания

к выполнению лабораторных работ дисциплины

«Математика» по направлению 110800.62 «Агроинженерия», профилю «Электроснабжение и электрооборудование сельхозпредприятий», направлению 140400.62 «Электроэнергетика и электротехника», профилям «Электромеханика», «Электропривод и автоматика» и направлению 20400.62 «Управление в технических системах», профилю «Управление и информатика в технических системах», очной формы обучения

Часть 2

Воронеж 2012

Составители: канд. физ.-мат. наук А.А. Катрахова, канд. физ.-мат. наук В.С. Купцов, канд. физ.-мат. наук А.В. Купцов

УДК 517.53

Методические указания к выполнению лабораторных работ дисциплины «Математика» по направлению 110800.62 «Агроинженерия», профилю «Электроснабжение и электрооборудование сельхозпредприятий», направлению 140400.62 «Электроэнергетика и электротехника», профилям «Электромеханика», «Электропривод и автоматика» и направлению 20400.62 «Управление в технических системах», профилю «Управление и информатика в технических системах», очной формы обучения. Ч. 2 / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. А.А. Катрахова, В.С.Купцов, А.В. Купцов. Воронеж: 2012. -34 c.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлениям 110800.62 «Агроинженерия», 140400.62 «Электроэнергетика и электротехника», 20400.62 «Управление в технических системах», дисциплине «Математика».

Предназначено для студентов первого, второго курсов.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word и содержатся в файле

«Lab2. doc»

Табл. 7. Ил.3 . Библиогр.: 10 назв.

Рецензент канд. физ.-мат. наук, доц. М.В. Юрьева

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета

Воронежского государственного технического университета

 ФГБОУ ВПО «Воронежский государственный технический университет», 2012

Лабораторная работа № 7 интерполяция функции многочленами лагранжа

Задание. Вычислить приближенное значение функции при данном значении аргумента х* с помощью интер­поляционного многочлена Лагранжа; построить график мно­гочлена Лагранжа, проходящий через заданные шесть точек.

Краткое описание метода.

Начнем с рассмотрения задачи интерполяции в наиболее простом и полно исследованном случае интерполирования алгебраическими многочленами. Для заданной таблицы данных)

(7.1)

интерполяционным многочленом, если он удовлетворяет условиям

(7.2)

Равенство (7.2) можно записать в виде системы уравнений

(7.3)

относительно коэффициентов многочлена а_к . Эта система однозначно разрешима, так как система функций 1, х, х²,…х^п линейно независима в точках х₀, х_и .х_п. Однозначная разрешимость системы(7.3) следует из того хорошо известного факта, что определитель этой системы (определитель Вандермонда)

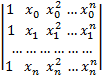
отличен от нуля, если узлы интерполяции попарно различны. Таким образом, верна следующая теорема.

Теорема 7.1. Существует единственный интерполяционный многочлен степени п, удовлетворяющий условиям (7.2).

Замечание. На практике система (7.3) никогда не используется для вычисления коэффициентов интерполяционного многочлена. Дело в том, что она часто является плохо обусловленной. Кроме того, существуют различные удобные явные формы записи интерполяционного многочлена, которые и применяются при интерполяции. Наконец, в большинстве приложений интерполяционного многочлена явное вычисление коэффициентов а_к не нужно.

Задача интерполяции состоит в построении функции (x) удовлетворяющей условию Другими словами, ставится задача о построении функции, график которой проходит через заданные точки (x_i,y_i) Так как функция (x) проходит через все заданные точки, то этот метод называется глобальной интерполяцией. Наиболее простой и полно исследованный случай - интерполяция алгебраическими многочленами. Одна из форм записи интерполяционного многочлена -многочлен Лагранжа:

Как нетрудно видеть, представляет собой многочлен, удовлетворяющий условиям

Таким образом, многочлен Лагранжа действительно является интерполяционным.

В инженерной практике наиболее часто используется интерполяция многочленами первой, второй и третьей степени. Приведем соответствующие формулы для записи многочленов Лагранжа первой и второй степени:

, (7.4)

(7.5)

Пример 7.1. Пусть задана таблица значений функции у=ln x :

X	1,0	1,1	1,2	1,3	1,4
У	0,000000	0,095310	0,182322	0,262364	0,336472

Для приближенного вычисления значения 1п(1,23) воспользуемся линейной и квадратичной интерполяцией.

Возьмем х₀=1,2 и x₁ =1,3. Вычисление по формуле (7.4) дает значение 1n(1,23) 0,206335 .

Для применения квадратичной интерполяции возьмем х₀ =1,1, x₁ =1,2, х₂ =1,3 - три ближайших к точке х =1,23

узла. Вычисляя по формуле (7.5), имеем 1n(1,23) 0,207066.

Приведем без доказательства наиболее известную теорему о погрешности интерполяции.

Теорема 7.1. Пусть функция f(x) дифференцируема n+1

раз на отрезке [а, b], содержащем узлы интерполяции Тогда для погрешности интерполяции в точке справедливо равенство

(7.6)

в котором

-некоторая точка, принадлежащая интервалу (а, b).

Основное неудобство в использовании этой теоремы состоит в том, что точка неизвестна. Поэтому чаще всего используется не сама теорема, а ее следствие.

Следствие. Справедлива оценка погрешности интерполяции в точке , имеющая, вид

(7.7)

а также оценка максимума модуля погрешности интерполяции на отрезке [a,b] имеющая вид

(7.8)

Пример 7.2. Оценим погрешность приближений к

ln(1,23) , полученных в примере 7.1 с помощью интерполяции многочленами первой и второй степени. В этих случаях неравенство (7.7) примет вид

(7.9)

Заметим, что для имеем и . Поэтому здесь

Тогда в силу неравенств (7.9) и(7.10) получаем следующие оценки погрешности:

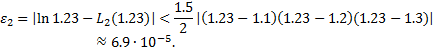
Если на отрезке [a,b], производная меняется слабо, то величина абсолютной погрешности почти полностью определяется значением функции . Представление о типичном характере поведения этой функции можно получить из рис. 1. Обратим внимание на то, что при выходе аргумента х за пределы отрезка наблюдения значение быстро становится очень большим. Это объясняет ненадежность экстраполяции функции для значений аргумента, удаленных от отрезка наблюдения.

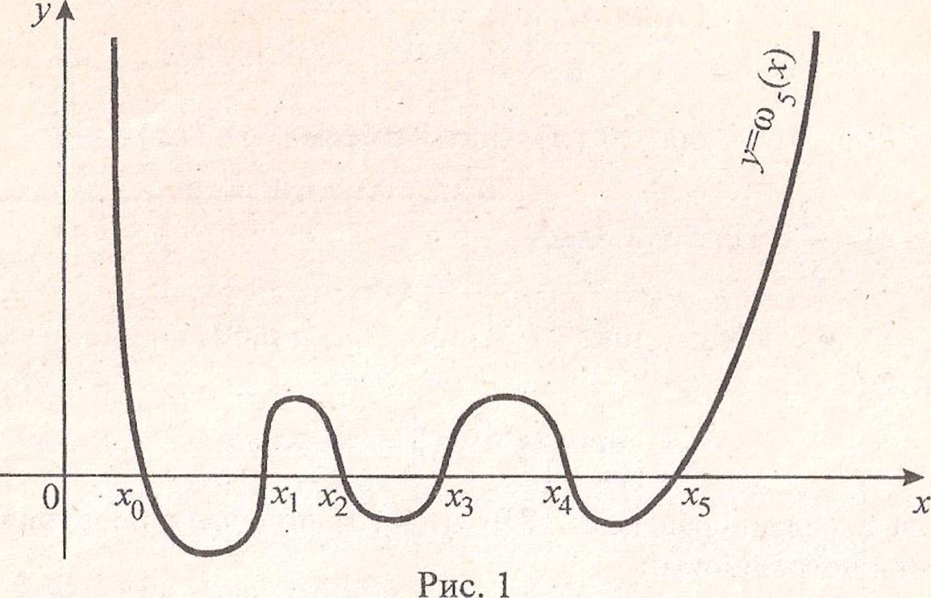
Рис.1.

Пусть теперь и пусть i-й шаг таблицы, а Несколько огрубляя оценку (7.8), можно получить следующее неравенство

Оно позволяет утверждать, что для достаточно гладкой функции при фиксированной степени интерполяционного многочлена погрешность интерполяции на отрезке [х₀, х_n] при стремится к нулю не медленнее, чем некоторая величина, пропорциональная . Этот факт принято формулировать так: интерполяция многочленом степени п имеет (n+1)-й порядок точности относительно h_max. В частности, линейная и квадратичная интерполяция имеют второй и третий порядок точности соответственно.

Варианты	x*	xi	yi	Варианты	x*	xi	yi
1	0,702	0,43 0,48 0,55 0,62 0,70 0,75	1,63597 1,73234 1,87686 2,03345 2,22846 2,35973	2	0,152	0,02 0,08 0,12 0,17 0,23 0,30	1,02316 1,09590 1,14725 1,21483 1,30120 1,40976
7	0,512			8	0,174
13	0,645			14	0,185
19	0,736			20	0,203
3	0,526	0,35 0,41 0,47 0,51 0,56 0,64	2,73951 2,30080 1,96864 1,78776 1,59502 1,34310	4	0,616	0,41 0,46 0,52 0,60 0,65 0,72	2,57418 2,32513 2,09336 1,?6203 1,74260 1,62098
9	0,453			10	0,478
. 15	0,482			16	0,665
21	0,552			22	0,537
5	0,896	0,68 0,73 0,80 0,88 0,93 0,99	0.80866 0,89492 1,02964 1,20966 1,34087 1,52368	6	0,314	0,11 0,15 0,21 0,29 0,35 0.40	9,05421 6,61659 4,69170 3,35106 2,73951 2,36522
11	0,812			12	0,235
17	0,774			18	0,332
23	0,915			24	0,275

Алгоритм программы

Использовать модули crt и graph;

определение переменных;

начало исполняемой части программы

задание значений элементов массивов х[i] и y[i]; задание значения аргумента хz; уz = 0; в цикле по i от 0 до 5 выполнять

| хх = 1;

| в цикле по ] от 0 до 5 выполнять если * / то |хх =хх (хz - х[j]/(х[i] - х[j]);

| y z =y z+y[i] x x

конец цикла по i;

вывод на экран значений хz и уz;.

ожидание нажатия клавиши Еnter;

переход в графический режим;

изображение заданных точек (х_i,у_i);

изображение графика многочлена Лагранжа;

ожидание нажатия любой клавиши конец программы.

Указание. При работе в графическом режиме воспользуйтесь программами из предыдущих лабораторных работ.

Контрольные вопросы

1. В чем состоит задача интерполяции?

2. Какой многочлен называется интерполяционным мно­гочленом ?

3. В чем состоит различие между глобальной и локаль­ной интерполяцией?

4. Как зависит степень интерполяционного многочлена Лагранжа от числа узлов?

5. Сколько многочленов существует, удовлетворяющих условию интерполирования?

6. В чем состоят недостатки интерполяционного много­члена Лагранжа?

7. Как оценивается погрешность интерполяции?

8. Как изменяется точность интерполяции в зависимости от расстояния от отрезка наблюдения и почему?