
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
14.5. Угол между двумя прямыми.
.Пусть
прямые
заданы уравнениями с угловым коэффициентом
у = k1х+
b1
и у = k2x
+ b2;
и EMBED Equation.3
![]() =
- угол между прямыми. Тогда
=
- угол между прямыми. Тогда
EMBED
Equation.3
![]() (14.9)
(14.9)
Прямые
параллельны, если EMBED Equation.3
![]() = 0, и условие параллельности
= 0, и условие параллельности
EMBED
Equation.3
![]() (14.10)
(14.10)
Условие
перпендикулярности – это условие того,
что tgj
не существует, т.е. 1 + EMBED Equation.3
![]() = 0, отсюда
условие
перпендикулярности
= 0, отсюда
условие
перпендикулярности
EMBED
Equation.3
![]() (14.11)
(14.11)
Пример 14.6. Определить угол между прямыми
у=2x+5 и у=-3х+1:
EMBED Equation.3
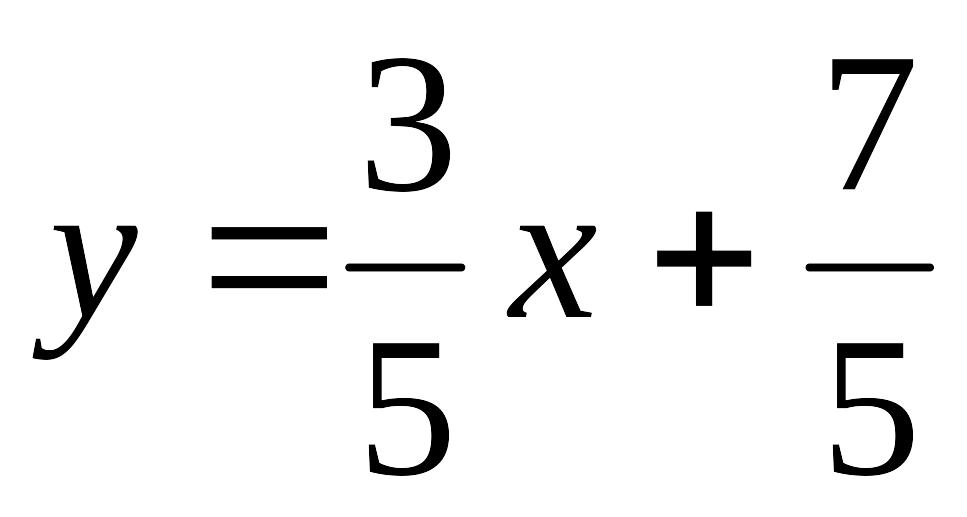 и EMBED Equation.3
и EMBED Equation.3
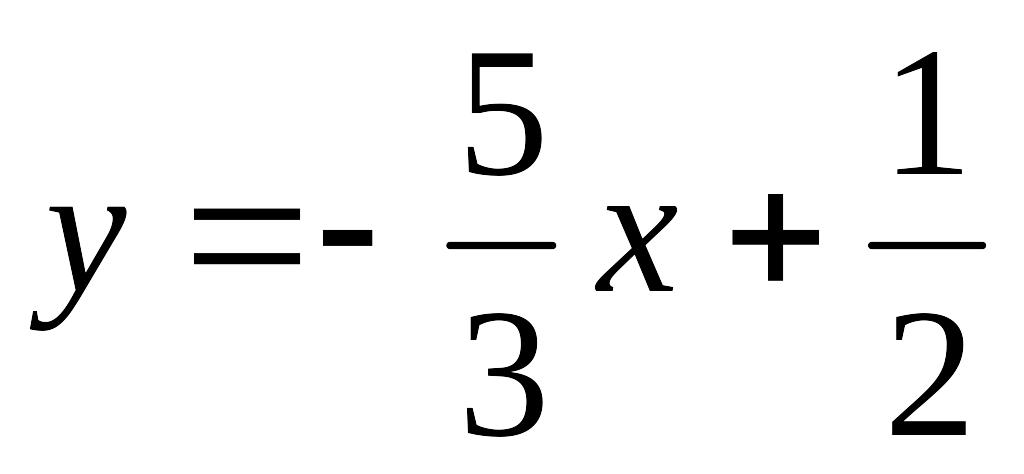
Решение.
1) В формуле
EMBED Equation.3
![]() принимаем
EMBED Equation.3
принимаем
EMBED Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() ,
тогда
EMBED Equation.3
,
тогда
EMBED Equation.3
![]() ,
т. e
EMBED Equation.3
,
т. e
EMBED Equation.3
![]() .
.
.2)
Здесь EMBED Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() .
Так как
EMBED Equation.3
.
Так как
EMBED Equation.3
![]() ,
то прямые перпендикулярны.
,
то прямые перпендикулярны.
Пример. 14.7. Даны уравнения высот треугольника АВС: x+y -2 = 0; 9x - 3y-4=0 и координаты вершины A(2; 2). Составить уравнения сторон треугольника.
Решение. Легко убедиться в том, что вершина А не лежит ни на одной из заданных высот: ее координаты не удовлетворяют уравнениям этих высот.
Пусть
9x
– 3у –
4 = 0 - уравнение высоты ВВ1
и x+y
-2=0 - уравнение высоты СС1.
Составим уравнение стороны АС,
рассматривая ее как прямую, проходящую
через точку А
и перпендикулярную высоте ВВ1.
Так как угловой коэффициент высоты
ВВ1
равен 3, то угловой коэффициент стороны
АС
равен -1/3, т. е. kAC=-1/3
. Воспользовавшись уравнением прямой,
проходящей через данную точку и имеющей
данный угловой коэффициент, получим
уравнение стороны АC:
y-2=-1/3(x-2),
или x
+ 3y
– 8 = 0. Аналогично получаем k
EMBED Equation.3
![]() ,
kAB=1
и сторона АВ
определится уравнением у
– 2 = x
- 2, т. е. у = х.
Решив совместно уравнения прямых АВ
и ВВ1
а также прямых АС
и СС1,
найдем координаты вершин треугольника
В
и С:
В(2/3;2/3)
и С(-1;3).
Остается составить уравнение стороны
ВС:
,
kAB=1
и сторона АВ
определится уравнением у
– 2 = x
- 2, т. е. у = х.
Решив совместно уравнения прямых АВ
и ВВ1
а также прямых АС
и СС1,
найдем координаты вершин треугольника
В
и С:
В(2/3;2/3)
и С(-1;3).
Остается составить уравнение стороны
ВС:
EMBED
Equation.3
![]() ,
т.е.7x
+ 5y
– 8 = 0.
,
т.е.7x
+ 5y
– 8 = 0.
Вопросы для самопроверки
Как записывается общее уравнение прямой на плоскости?
Как записываются параметрические уравнения прямой на плоскости?
Что называется угловым коэффициентом прямой на плоскости и каков его геометрический смысл в декартовой прямоугольной системе координат?
Как записывается уравнение прямой, проходящей через две точки на плоскости?
Как вычисляются углы между двумя прямыми на плоскости? Каковы условия параллельности и перпендикулярности двух прямых на плоскости?
Задачи для самостоятельного решения
1.
Дано уравнение прямой
EMBED Equation.3
![]() .
.
Написать: а) общее уравнение этой прямой; б) уравнение с угловым коэффициентом; в) уравнение в отрезках; г) нормальное уравнение.
Ответ:
а)
EMBED Equation.3
![]() ;
б)
EMBED Equation.3
;
б)
EMBED Equation.3
![]() ;
в) EMBED Equation.3
;
в) EMBED Equation.3
![]() ;
г) EMBED Equation.3
;
г) EMBED Equation.3
![]()
2. Прямая отсекает на осях координат равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного прямой с осями координат, равна 8.
Ответ. х + y - 4 = 0.
3.
Даны вершины треугольника АВС
: EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]()
EMBED
Equation.3
![]() Определить
внутренний угол при вершине А.
Определить
внутренний угол при вершине А.
Ответ.
EMBED Equation.3
![]() .
.
4.
Даны стороны треугольника: EMBED Equation.3
![]() ,
,
EMBED
Equation.3
![]() .
Составить уравнения его высот.
.
Составить уравнения его высот.
Ответ.
EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() .
.
5.
Даны вершины треугольника EMBED Equation.3
![]() Составить уравнения медианы, проведенной
из вершины В
,и высоты,
опущенной из вершины С
. Вычислить площадь треугольника.
Составить уравнения медианы, проведенной
из вершины В
,и высоты,
опущенной из вершины С
. Вычислить площадь треугольника.
Ответ.
EMBED Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() кв.ед.
кв.ед.
6. Даны вершины треугольника АВС: А(0;2), B(7;3) и С(1;6). Определить ВАС=.
Ответ.
EMBED Equation.3
![]()
7. Даны стороны треугольника x + y - 6=0, 3x - 5y+14=0 и 5x -3y -14=0. Составить уравнения высот треугольника.
Ответ. x-y = 0, 5x +3y -26 = 0, 3x +5y – 26 = 0.
8.. Составить уравнения биссектрис углов между прямыми 3x +4y – 20 = 0 и 8x+6y + 35 = 0.
Ответ. 14x +14y – 45 = 0, 2x - 2y + 35 = 0.
9. Даны вершины треугольника: А(0;0), В(-1;-3) и С(-5;-1). Составить уравнения прямых, проходящих через вершины треугольника и параллельных сторонам треугольника.
Ответ. 3x – y +14 = 0, x - 5y -14 = 0, x +2y = 0
10. Определить расстояние от точки М(2;-1)до прямой, отсекающей на осях координат отрезки а =8, b=6.
Ответ. 4,4.
11. Найти длину высоты треугольника с вершинами A(3/2;1), B(1;5/3), С(3;3), проведенной из вершины С.
Ответ. 2,4.
12. Даны середины сторон треугольника: A1(-1;-1), B1(1;9), C1(9;1). Составить уравнения перпендикуляров к сторонам, проходящих через середины соответствующих сторон треугольника.
Ответ. х –y = 0, x + 5y – 14 = 0, 5x +y – 14 = 0.
13. Найти острый угол, образованный с осью ординат прямой, проходящей через точки:
А(2;
EMBED Equation.3
![]() )
и B(3;
EMBED Equation.3
)
и B(3;
EMBED Equation.3
![]() ).
).
Ответ.
EMBED Equation.3
![]()
14. Точки А(1;2) и С(3;6) являются противоположными вершинами квадрата. Определить координаты двух других вершин квадрата.
Ответ. (0;5) и (4;3).
15. Найти прямую, проходящую через точку пересечения прямых x +2y +3 = 0, 2x +3y +4 = 0 и параллельную прямой
5x +8y = 0.
Ответ. 5х +8у +11 = 0.
16. Показать, что треугольник со сторонами х +y EMBED Equation.3 +1=0, x EMBED Equation.3 + y+1 = 0 и x –y -10 = 0 равнобедренный. Найти угол при вершине треугольника.
Ответ. 30°.
17. Дана вершина треугольника A(3;9) и уравнения медиан: у – 6 = 0 и 3х - 4y +9 = 0. Найти координаты двух других вершин.
Ответ. В(1;3), С(11;6).
18. Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой
4x +3y -12 = 0, концы которого лежат на осях координат.
Ответ. 3х - 4у -9 = 0, 3х - 4у +16 = 0, 4x +3y -37 = 0 или
4х +3у +13 = 0.
Занятие 15. Кривые второго порядка: окружность, эллипс
15.1. Окружность.
Окружность-это геометрическое место точек, равноудаленных от данной точки (центра) . Если r-радиус окружности, а точка С(a; b)-ее центр то уравнение окружности имеет вид
(x-a)²+(y-b)²= r². (15.1)
В частности, если центр окружности совпадает с началом координат, то последнее уравнение примет вид
x² + y² = r² .
Полезно помнить, что уравнение окружности содержит старшие члены x² и y² с равными коэффициентами и в нем отсутствует член с произведением x на y.
Пример 15.1. Найти координаты центра и радиус окружности 2x² + 2y² - 8х- 5у-4=0.
Решение.
Разделив уравнение на 2 и сгруппировав
члены уравнения, получим EMBED Equation.3
![]() .
Дополним x²
-4х
и y²+
EMBED Equation.3
.
Дополним x²
-4х
и y²+
EMBED Equation.3
![]() до полных квадратов, прибавив к первому
двучлену 4 и ко второму EMBED Equation.3
до полных квадратов, прибавив к первому
двучлену 4 и ко второму EMBED Equation.3
![]() (одновременно к правой части прибавляется
сумма этих чисел):
(одновременно к правой части прибавляется
сумма этих чисел):
EMBED
Equation.3
![]()
или
EMBED
Equation.3
![]()
Таким образом, координаты центра окружности а = 2,
b= -5/4 и радиус окружности r =11/4.
Пример 15.2. Составить уравнение окружности, описанной около треугольника, стороны которого заданны уравнениями.
9х -2у – 41 = 0, 7х +4у + 7 = 0, х -3у +1= 0.
Решение. Найдём координаты вершин треугольника, решив совместно три системы уравнений:
1)
EMBED Equation.3
![]()
2)
EMBED Equation.3
![]()
3)
EMBED Equation.3
![]()
Получим А(3,-7), В(5,2), С(-1,0).
Пусть искомое уравнение окружности имеет вид
(x - а)²+(y - b)²=r². Для нахождения a, b, r напишем три равенства, подставив в искомое уравнение вместо текущих координат координаты точек А, В, С:
EMBED
Equation.DSMT4

Исключая r², приходим к системе уравнений:
EMBED
Equation.DSMT4
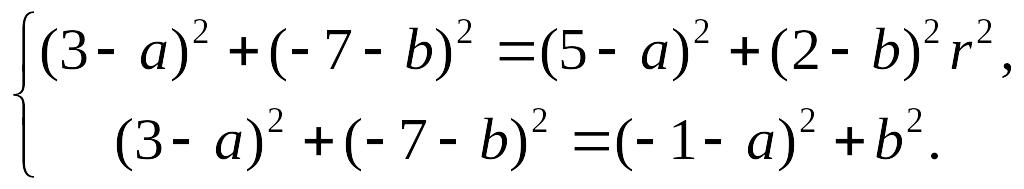
Или 4а + 18 b = -29 и 8а – 14b=57. Отсюда, а=3,1, b = -2,3. Значение r² находим из уравнения (-1 - а) 2+b2 = r², т.е. r²=22,1; уравнение искомой окружности (х-3,1)2 +(у+2,3) 2 =22,1.
Пример 15.3. Составить уравнение окружности, проходящей через точки А(5,0) и В(1,4), если центр её лежит на прямой х +у – 3 = 0.
Решение. Найдём координаты точки М – середины хорды АВ:
EMBED
Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() ,
т.е. середина хорды АВ
– точка М(3,2).
Центр окружности должен находиться на
перпендикуляре, восстановленном из
середины хорды, поэтому уравнение этого
перпендикуляра можно записать в виде:
,
т.е. середина хорды АВ
– точка М(3,2).
Центр окружности должен находиться на
перпендикуляре, восстановленном из
середины хорды, поэтому уравнение этого
перпендикуляра можно записать в виде:
у
– 2 = k
(х
-3), где угловой коэффициент k
найдётся из условия перпендикулярности
с прямой АВ,
уравнение которой EMBED Equation.3
![]() или х +
у
-5 = 0.
или х +
у
-5 = 0.
Следовательно, угловой коэффициент перпендикуляра k=1, а уравнение этого перпендикуляра у -2 = 1(х -3), или
х – у -1 = 0.
Центр окружности С лежит на пересечении данной прямой с перпендикуляром, т.е. координаты центра определяются из решения системы уравнений х + у – 3 = 0 и х – у -1 = 0. Отсюда х =2, у =1, т.е. С(2,1).
Радиус
окружности равен длине отрезка СА,
т.е. EMBED Equation.3
![]() .
Итак, уравнение окружности
.
Итак, уравнение окружности
(х-2) 2+ (у -1) 2 = 10.
