
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
13.1. Условие принадлежности двух прямых к одной плоскости.
Две прямые в пространстве могут:
пересекаться;
быть параллельными;
скрещиваться.
В первых двух случаях прямые лежат в одной плоскости.
Пусть
прямые EMBED Equation.3
![]() и EMBED Equation.3
и EMBED Equation.3
![]() заданы каноническими уравнениями:
заданы каноническими уравнениями:
EMBED
Equation.3
![]() ;
EMBED Equation.3
;
EMBED Equation.3
![]() .
.
Для принадлежности двух прямых к одной плоскости необходимо и достаточно, чтобы три вектора
EMBED
Equation.3
![]() ,
( EMBED Equation.3
и EMBED Equation.3
точки на прямых EMBED Equation.3
,
( EMBED Equation.3
и EMBED Equation.3
точки на прямых EMBED Equation.3
![]() и EMBED Equation.3
),
EMBED Equation.3
и EMBED Equation.3
),
EMBED Equation.3
![]() были компланарны, т.е. смешанное
произведение этих векторов равно нулю
были компланарны, т.е. смешанное
произведение этих векторов равно нулю
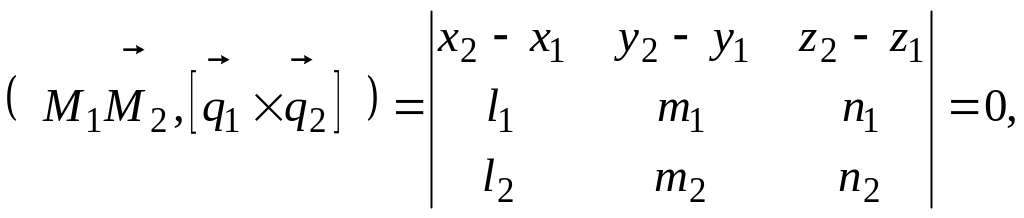
(13.1) Пример 13.1. Доказать, что прямые пересекаются.
EMBED Equation.3
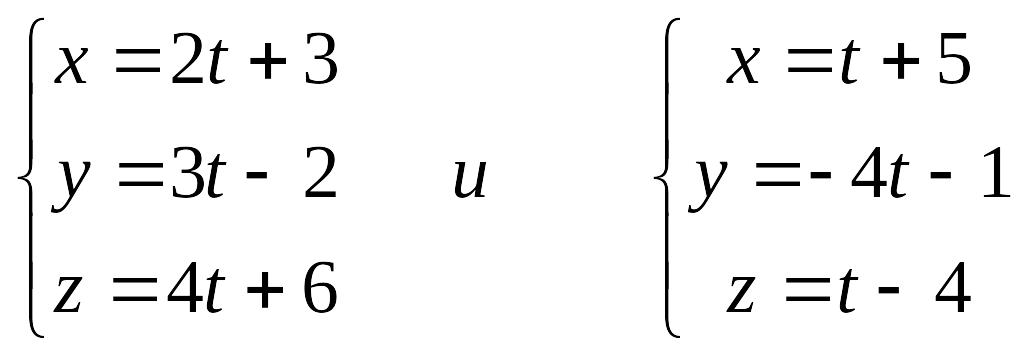
Решение. Применим формулу (4.1).
EMBED Equation.3
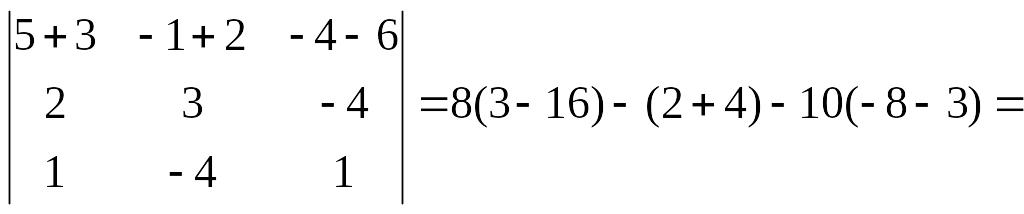
=-104 – 6 + 110 = 0.
Таким образом, прямые лежат в одной плоскости. А так как координаты их направляющих векторов не пропорциональны, следовательно, прямые не параллельны, а пересекаются. Что и требовалось доказать.
13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
Рассмотрим
плоскость p,
заданную уравнением EMBED Equation.3
![]() и прямую EMBED Equation.3
и прямую EMBED Equation.3
![]() ,
заданную каноническими уравнениями:
,
заданную каноническими уравнениями:
EMBED
Equation.3
![]()
Поскольку
угол j
между прямой EMBED Equation.3
и плоскость p
является дополнительным к углу между
вектором нормали плоскости EMBED Equation.3
![]() и
направляющим вектором прямой EMBED
Equation.3
и
направляющим вектором прямой EMBED
Equation.3
![]() ,
то ( EMBED Equation.3
,
EMBED Equation.3
)=
EMBED Equation.3
,
то ( EMBED Equation.3
,
EMBED Equation.3
)=
EMBED Equation.3
![]() ; cosy
= cos(900
- j)
= sinj,
тогда
; cosy
= cos(900
- j)
= sinj,
тогда
EMBED
Equation.3
![]() (13.2)
(13.2)
Условие параллельности прямой и плоскости эквивалентно условию перпендикулярности направляющего вектора прямой и нормального вектора плоскости
Аl +Bm +Cn = 0 (13.3)
Условие
перпендикулярности прямой и плоскости
эквивалентно условию параллельности
EMBED Equation.3
и EMBED Equation.3
![]()
EMBED Equation.3
![]() (13.4)
(13.4)
Пример
13.2. При каком
значении EMBED Equation.3
![]() и
EMBED Equation.3
и
EMBED Equation.3
![]() прямая
прямая
EMBED
Equation.3
![]() и
плоскость EMBED Equation.3
и
плоскость EMBED Equation.3
![]() перпендикулярны?
перпендикулярны?
Решение.
Воспользуемся условием перпендикулярности
прямой и плоскости (4.4). Тогда EMBED
Equation.3
![]() .
Получаем EMBED Equation.3
.
Получаем EMBED Equation.3
![]()
Пример 13.3. При каком значении n прямая
EMBED Equation.3
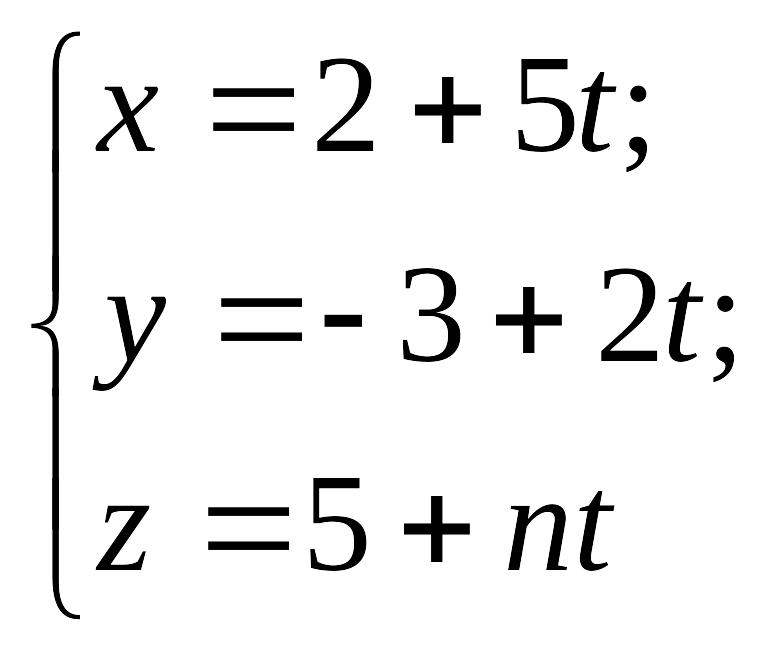 параллельна плоскости EMBED Equation.3
параллельна плоскости EMBED Equation.3
![]() .
.
Решение.
Обращаемся
к условию параллельности прямой и
плоскости (4.3). Подставляя соответствующие
значения в это уравнение, получим EMBED
Equation.3
![]() или
или
EMBED
Equation.3
![]() откуда
EMBED Equation.3
откуда
EMBED Equation.3
![]()
13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
Условие
принадлежности прямой
EMBED Equation.3
к
плоскости
EMBED Equation.3
![]() выражается
двумя равенствами
выражается
двумя равенствами
EMBED
Equation.3
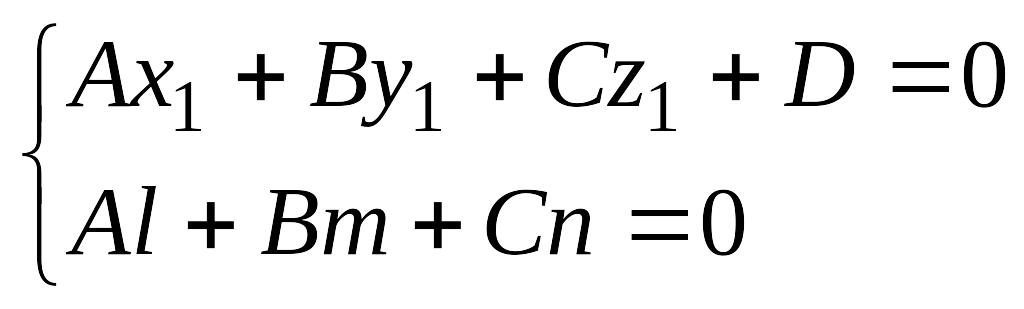 ,
(13.5)
,
(13.5)
первое из которых означает, что точка EMBED Equation.3 (x1,y1,z1), через которую проходит прямая, принадлежит плоскости, а второе- это условие параллельности прямой и плоскости.
Координаты
точки пересечения прямой
EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() и плоскости
Ax+By+Cz+D=0
определяются
из системы уравнений
и плоскости
Ax+By+Cz+D=0
определяются
из системы уравнений
EMBED Equation.3
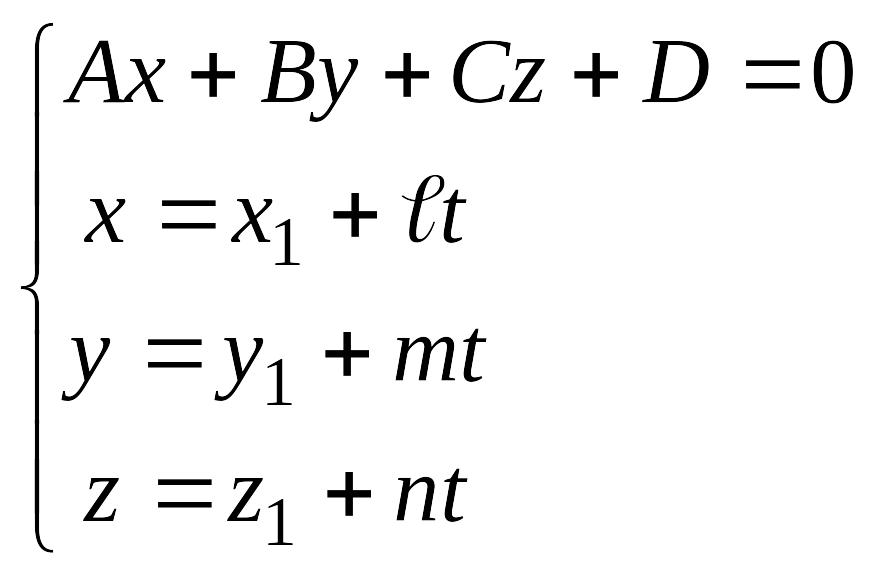 (13.6)
(13.6)
Пример 13.4. Доказать, что прямая
EMBED
Equation.3
![]() лежит в плоскости
лежит в плоскости
3x+2y-4z-23=0.
Решение. Воспользуемся формулой (4.5)
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]() .
.
Следовательно, прямая лежит в данной плоскости.
Пример
13.5. Найти
точку пересечения плоскости EMBED
Equation.3
![]() и прямой EMBED Equation.3
и прямой EMBED Equation.3
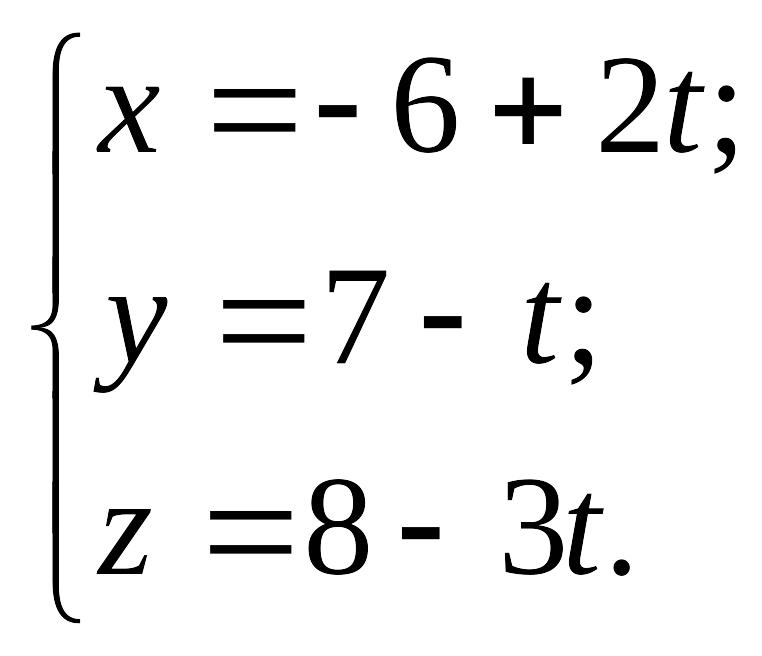
Решение.
Решим
совместно систему уравнений прямой и
плоскости. Подставим выражение для
EMBED Equation.3
![]() в уравнение плоскости
в уравнение плоскости
EMBED
Equation.3
![]()
После
упрощения получим EMBED Equation.3
![]() откуда
EMBED Equation.3
откуда
EMBED Equation.3
![]() Из уравнения прямой при EMBED Equation.3
Из уравнения прямой при EMBED Equation.3
![]() находим координаты точки пересечения
EMBED Equation.3
находим координаты точки пересечения
EMBED Equation.3
![]() Таким
образом, искомой точкой пересечения
является точка EMBED Equation.3
Таким
образом, искомой точкой пересечения
является точка EMBED Equation.3
![]()
Пример
13.6. Дана
прямая EMBED
Equation.3
![]() и вне ее точка М
( 1; 1; 1). Найти
точку N,
симметричную точке М
относительно
данной прямой.
и вне ее точка М
( 1; 1; 1). Найти
точку N,
симметричную точке М
относительно
данной прямой.
Решение. Составим уравнение плоскости, проектирующей точку М на данную прямую, в виде
EMBED
Equation.DSMT4
![]()
Используя
условие перпендикулярности заданной
прямой и проектирующей плоскости EMBED
Equation.DSMT4
![]() ,
находим уравнение плоскости
,
находим уравнение плоскости
EMBED Equation.DSMT4
![]()
или
EMBED Equation.DSMT4
![]() .
.
Найдем проекцию точки М на прямую, для чего совместно решим систему уравнений
EMBED Equation.3
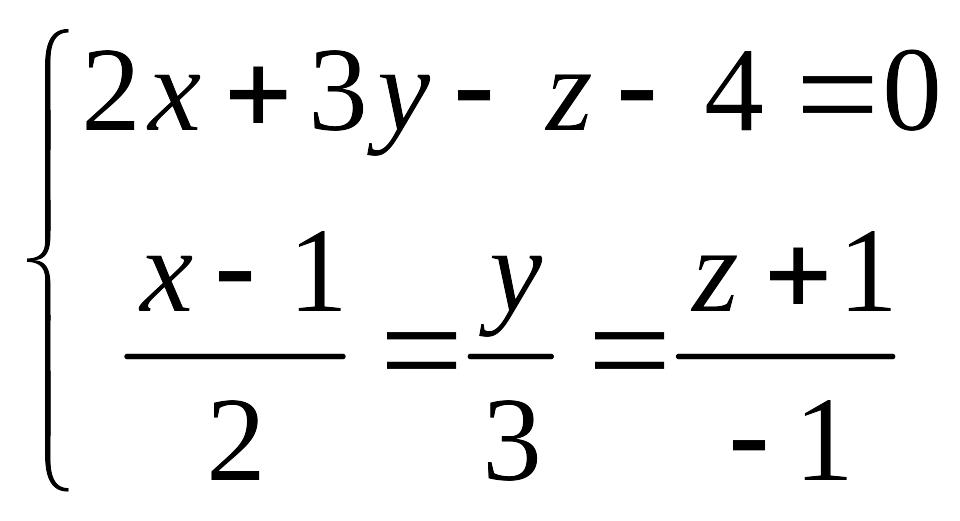
Запишем уравнения прямой в параметрическом виде
EMBED Equation.3
![]()
Подставляя x, y, z в уравнение плоскости, найдем t =1/14. Отсюда x =8/7, y =3/ 14, z =-15/14.
Тогда координаты симметричной точки можно найти из формул середины отрезка, т.е.
EMBED Equation.DSMT4
![]() ,
,
или
EMBED Equation.DSMT4
![]() ,
,
откуда
EMBED Equation.DSMT4
![]() ,
EMBED Equation.DSMT4
,
EMBED Equation.DSMT4
![]() ,
EMBED Equation.DSMT4
,
EMBED Equation.DSMT4
![]() .
Следовательно,
.
Следовательно,
N(9/7; - 4/7; - 22/7).
Пример 13.7. Вычислит расстояние d точки Р(1 -1;-2) от прямой
EMBED
Equation.3
![]()
Решение
1. Выберем
на прямой какую-нибудь точку, например
М1(
-3; -2; 8). Будем считать, что направляющий
вектор прямой EMBED Equation.DSMT4
![]() приложен в точке М1.
Модуль векторного произведения векторов
EMBED Equation.DSMT4
и EMBED Equation.DSMT4
приложен в точке М1.
Модуль векторного произведения векторов
EMBED Equation.DSMT4
и EMBED Equation.DSMT4
![]() определит площадь параллелограмма,
построенного на этих векторах; высота
этого параллелограмма, проведенная из
вершины Р
, будет являться искомым расстоянием
d.
Следовательно, для вычисления расстояния
d
имеем формулу EMBED Equation.DSMT4
определит площадь параллелограмма,
построенного на этих векторах; высота
этого параллелограмма, проведенная из
вершины Р
, будет являться искомым расстоянием
d.
Следовательно, для вычисления расстояния
d
имеем формулу EMBED Equation.DSMT4
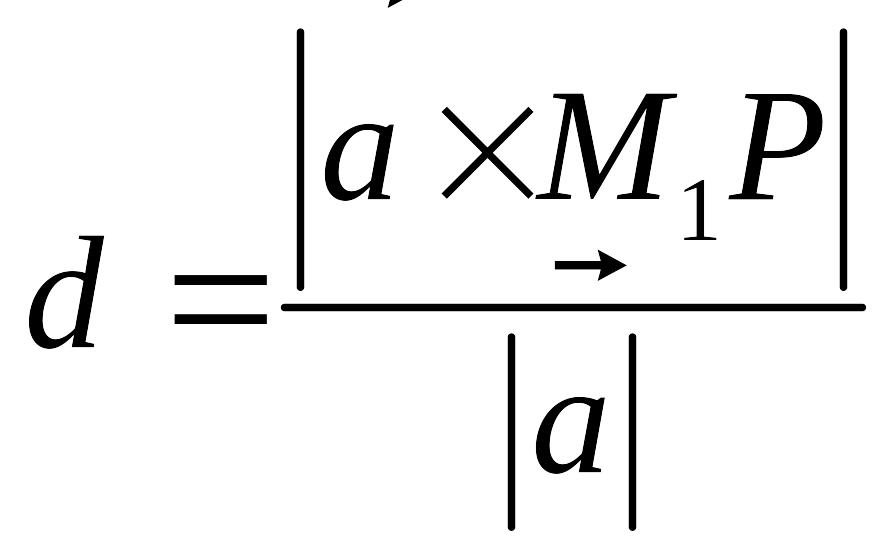 .
Теперь вычислим координаты вектора
EMBED Equation.DSMT4
,
зная координаты его конца и начала:
EMBED Equation.DSMT4
=
EMBED Equation.DSMT4
.
Теперь вычислим координаты вектора
EMBED Equation.DSMT4
,
зная координаты его конца и начала:
EMBED Equation.DSMT4
=
EMBED Equation.DSMT4
![]() .
Найдем векторное произведение векторов
EMBED Equation.DSMT4
и EMBED Equation.DSMT4
:
EMBED Equation.DSMT4
.
Найдем векторное произведение векторов
EMBED Equation.DSMT4
и EMBED Equation.DSMT4
:
EMBED Equation.DSMT4
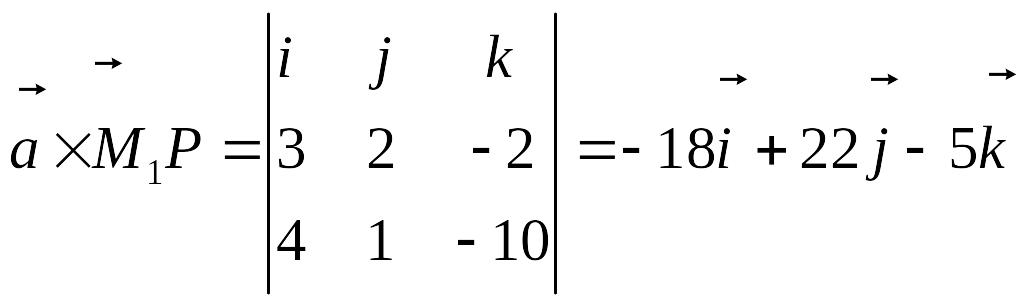 .
Определим его модуль EMBED Equation.DSMT4
.
Определим его модуль EMBED Equation.DSMT4
![]() .
Вычислим модуль вектора EMBED Equation.DSMT4
:
EMBED Equation.DSMT4
.
Вычислим модуль вектора EMBED Equation.DSMT4
:
EMBED Equation.DSMT4
![]() .
Найдем искомое расстояние EMBED
Equation.DSMT4
.
Найдем искомое расстояние EMBED
Equation.DSMT4
![]() .
.
Решение 2. Составим уравнение плоскости, проектирующей точку Р на данную прямую, в виде
EMBED
Equation.DSMT4
![]()
Используя
условие перпендикулярности заданной
прямой и проектирующей плоскости EMBED
Equation.DSMT4
![]() ,
находим уравнение плоскости
EMBED Equation.DSMT4
,
находим уравнение плоскости
EMBED Equation.DSMT4
![]() .
.
Найдем точку М пересечения прямой с построенной плоскостью. Для этого запишем уравнения прямой в параметрическом виде EMBED Equation.3
Подставляя x, y, z в уравнение плоскости, найдем t = 2. Отсюда x = 3, y =2, z =-4. Расстояние между точками Р и М будет являться искомым расстоянием d. Следовательно
EMBED
Equation.DSMT4
![]()
Пример 13.8. Вычислить кратчайшее расстояние между двумя прямыми
EMBED
Equation.3
![]() ;. EMBED Equation.3
;. EMBED Equation.3
![]() .
.
Решение.
Данные прямые
являются скрещивающимися и лежат в
параллельных плоскостях. Через прямую
l2проведем
плоскость параллельную прямой l1.
В качестве нормального вектора возьмем
EMBED Equation.DSMT4
![]() ,
где EMBED Equation.DSMT4
,
где EMBED Equation.DSMT4
![]() и EMBED Equation.DSMT4
и EMBED Equation.DSMT4
![]() -
направляющие векторы прямых.
-
направляющие векторы прямых.
EMBED
Equation.DSMT4
=
EMBED Equation.DSMT4
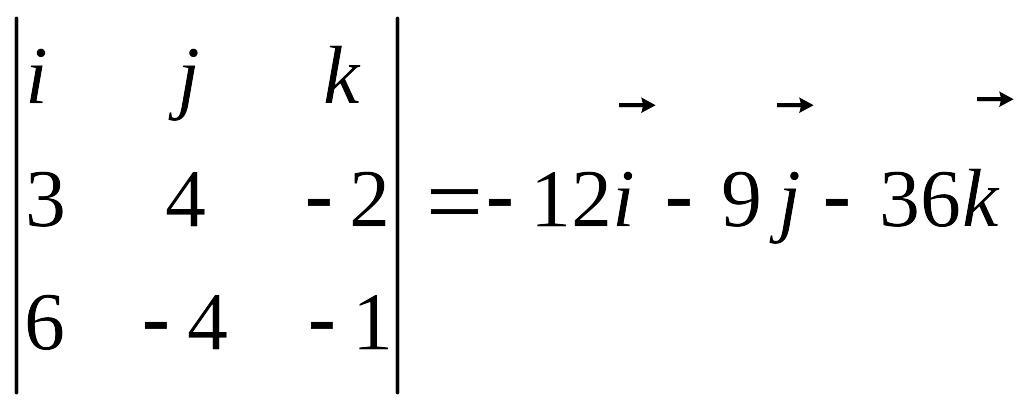
Зная точку на прямой l2 - М2(21;-5; 2), запишем уравнение плоскости в виде
EMBED
Equation.DSMT4
![]() или
или
EMBED
Equation.DSMT4
![]() .
.
Расстояние от точки М1(-7; -4; -3) на прямой l1 и будет искомым расстоянием:
EMBED
Equation.DSMT4
![]() .
.
