Алгебраические свойства скалярного произведения

1. _{EMBED Equation.3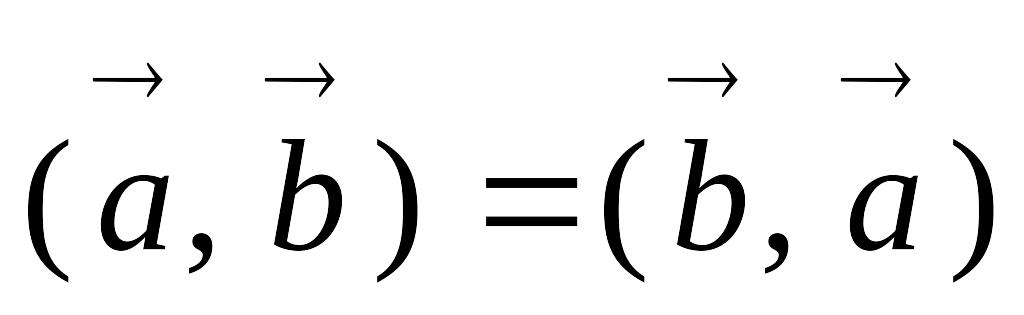} (переместительное свойство).

2. _{EMBED Equation.3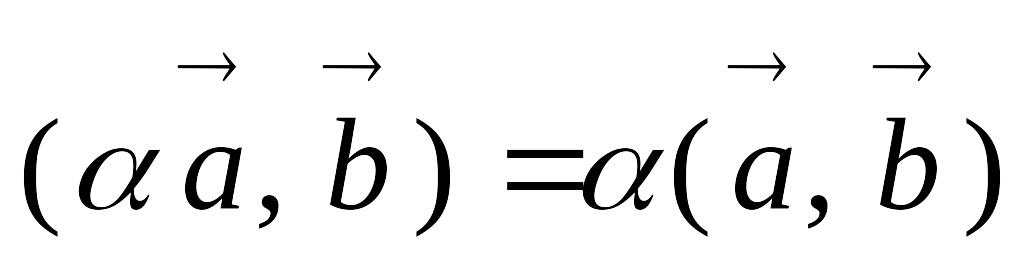} (сочетательное свойство относительно числового множителя).

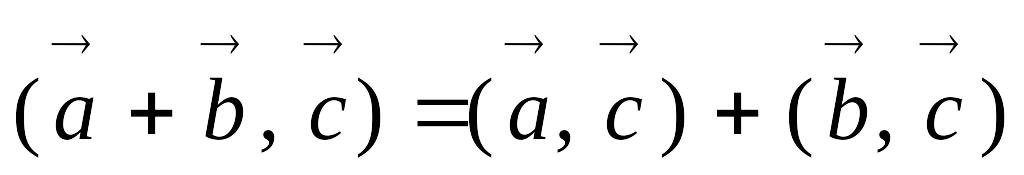3. _{EMBED Equation.3} (распределительное свойство относительно суммы векторов).

4. _{EMBED Equation.3} , если EMBED Equation.3 - ненулевой вектор,

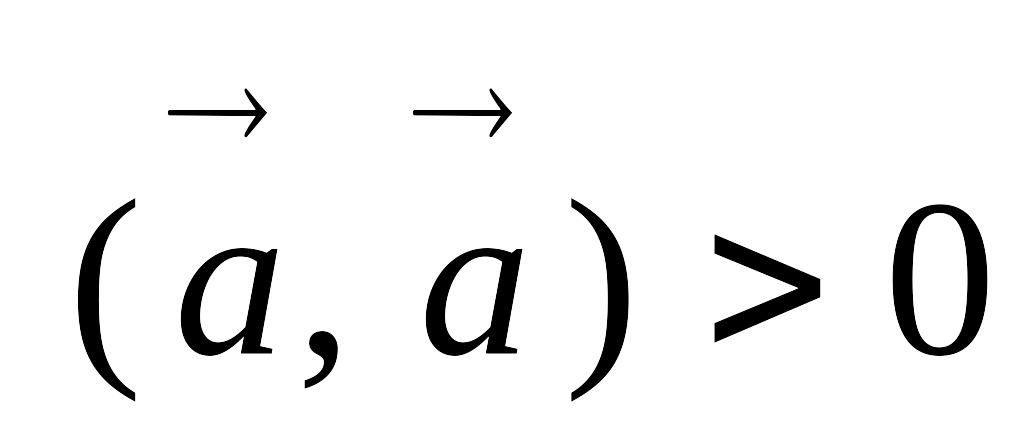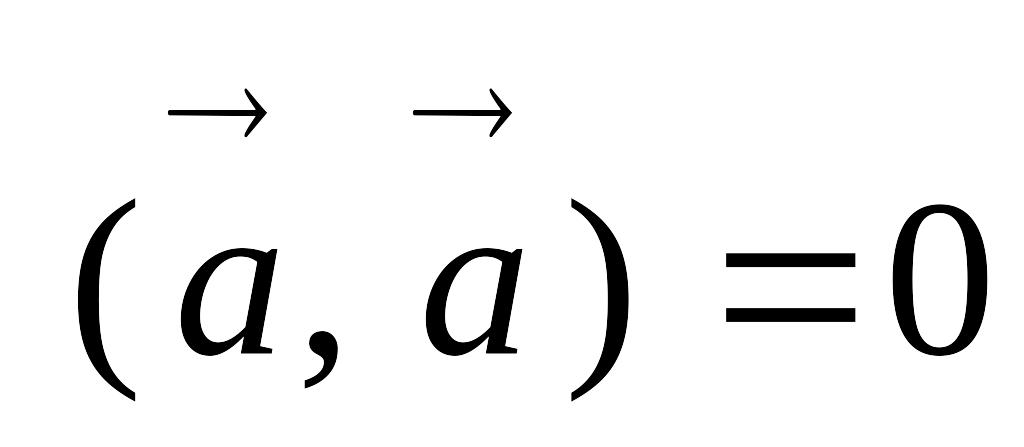5. _{EMBED Equation.3} , если EMBED Equation.3 - нулевой вектор.

Действительное векторное пространство с определенным нами скалярным произведением называется евклидовым пространством.

Теорема. Если два вектора EMBED Equation.3 и EMBED Equation.3 определены своими декартовыми прямоугольными координатами: EMBED Equation.3 ; EMBED Equation.3 , то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат, то есть

_{EMBED Equation.3} , (7.4)

отсюда

_{EMBED Equation.3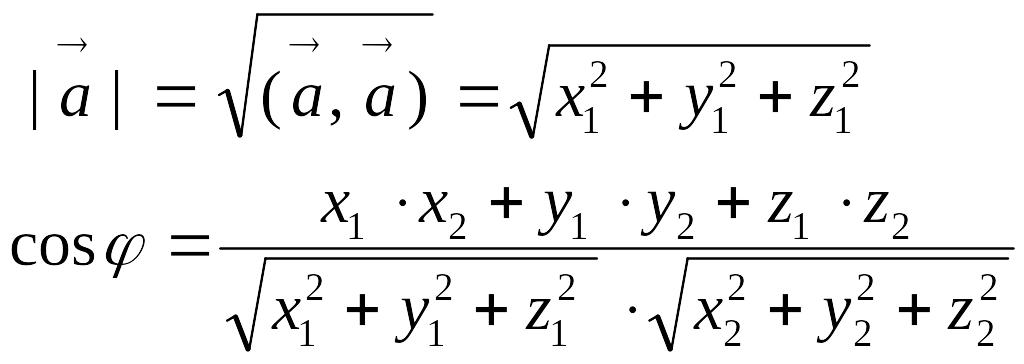} . (7.5)

Теорема доказывается путем скалярного перемножения многочленов

_{EMBED Equation.3}

_{EMBED Equation.3}

_{EMBED Equation.3}

Отметим, что скалярное произведение для системы единичных базисных векторов обладает свойством:

EMBED Equation.3 при EMBED Equation.3 , то есть

Следствие . Необходимым и достаточным условием ортогональности векторов EMBED Equation.3 и EMBED Equation.3 является равенство _{EMBED Equation.3} .

Пример 7.1. Какому условию должны удовлетворять векторы EMBED Equation.3 и EMBED Equation.3 , чтобы вектор EMBED Equation.3 был перпендикулярен вектору EMBED Equation.3 ?

Решение. Если EMBED Equation.3 , то EMBED Equation.3 .

Раскрывая скобки в последнем равенстве (в силу свойства скалярного произведения), получим

EMBED Equation.3 , откуда EMBED Equation.3 .

Пример 7.2. Дан треугольник с вершинами

EMBED Equation.3 (-3,5,6), EMBED Equation.3 (1,-5,7), EMBED Equation.3 (8,-3,-1). Найти внутренний угол при вершине EMBED Equation.3 .

Решение. Внутренний угол треугольника при вершине EMBED Equation.3 равен углу между векторами EMBED Equation.3 и EMBED Equation.3 .

Находим координаты указанных векторов:

EMBED Equation.3 , EMBED Equation.3 .

С помощью формулы (8.5) находим косинусы углов:

EMBED Equation.3 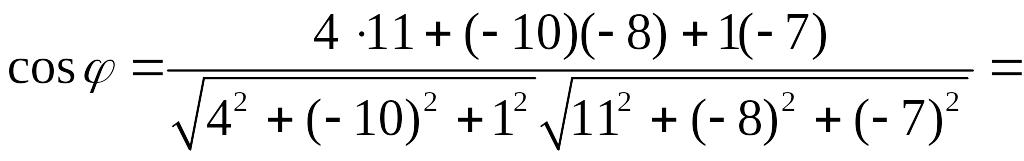_{EMBED Equation.3 .}

Следовательно, EMBED Equation.3 .

Пример 7.3. Даны три вектора EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3 . Найти EMBED Equation.3 .

Решение. Определим вектор:

EMBED Equation.3 ;

В соответствии с формулой находим:

EMBED Equation.3 .

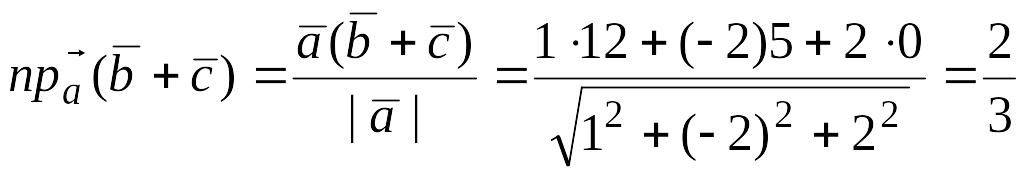Вопросы для самопроверки

1. Что называется скалярным произведением двух ветров, каковы его свойства?

2. Как скалярное произведение выражается через координаты векторов-сомножителей?

3. Каковы формулы длины вектора, угла между двумя векторами, расстояния между двумя точками в декартовой системе координат?

Задачи для самостоятельного решения

1. Векторы EMBED Equation.3 и EMBED Equation.3 образуют угол φ = 2π/3; зная, что

EMBED Equation.DSMT4 = 3, EMBED Equation.DSMT4 = 4, вычислить: 1) ( EMBED Equation.DSMT4 ; 2) EMBED Equation.DSMT4 ;

3) ( EMBED Equation.DSMT4 .

2. Даны векторы EMBED Equation.3 = { 4 ; -2 ; -4 } и EMBED Equation.3 = { 6 ;-3; 2 }. Вычислить: 1) EMBED Equation.DSMT4 ; 2) EMBED Equation.DSMT4 ; 3) EMBED Equation.DSMT4 .

3. . Найти внутренние углы треугольника с вершинами

A (5,2,-4), B (9,-8,-3), C (16,-6,-11).

4. Даны вершины четырехугольника А (1; -2; 2),

B (1; 4; 0), C (-4; 1; 1), D (-5; -5; 3). Доказать, что его диагонали взаимно перпендикулярны.

5. Определить, при каком значении α векторы EMBED Equation.DSMT4 и EMBED Equation.DSMT4 взаимно перпендикулярны.

6. Вычислить косинус угла, образованного векторами

EMBED Equation.3 = { 2; -4; 4} и EMBED Equation.3 = { -3; 2; 6}.

7.Вычислить внутренние углы треугольника с вершинами А (1; 2; 1), В (3; -1; 7). С (7; 4; -2), убедиться, что этот треугольник равнобедренный.

8. Вектор EMBED Equation.DSMT4 , перпендикулярный к векторам EMBED Equation.DSMT4 и EMBED Equation.DSMT4 образуют с осью Оу тупой угол. Найти его координаты, зная, что EMBED Equation.DSMT4 = 14.

9. Даны векторы EMBED Equation.3 = { 3; -1; 5} и EMBED Equation.3 = { 1; 2; -3}. Найти вектор EMBED Equation.DSMT4 при условии, что он перпендикулярен к оси Oz и удовлетворяет условиям EMBED Equation.DSMT4

10. Найти проекцию вектора EMBED Equation.3 = { 5; 2; 5} на ось вектора EMBED Equation.3 = { 2; -1; 2}.

11. Даны векторы EMBED Equation.3 = { 1; -3; 4}, EMBED Equation.3 = { 3; -4; 2}и

EMBED Equation.DSMT4 = { -1; 1; 4}. Вычислить EMBED Equation.DSMT4 .

12. Даны векторы EMBED Equation.3 = { -2; 1; 1}, EMBED Equation.3 = { 1; 5; 0} и

EMBED Equation.DSMT4 ={ 4; 4; -2}. Вычислить EMBED Equation.DSMT4 .

13. Даны точки M (-5; 7; -6) и N (7; -9; 9). Вычислить проекцию вектора. EMBED Equation.3 = { 1; -3; 1} на ось вектора EMBED Equation.DSMT4 .

14. Даны точки A (-2; 3; -4), B (3; 2; 5), C (1; -1; 2), D (3; 2; -4). Вычислить EMBED Equation.DSMT4 .

Ответы: 1. 1)13, 2)-61, 3) 73. 2. 1) -200, 2) 129, 3) 41. 3. EMBED Equation.3 ; EMBED Equation.3 . 5. α = -6. 6. cos φ =5/21. 8. EMBED Equation.DSMT4 = { -4; -6; 12}. 9. EMBED Equation.DSMT4 = { 2; -3; 0}. 10. 6. 11. 5. 12. -11. 13. 3. 14. -47/7.

Занятие 8. Векторное произведение векторов

Три вектора называются упорядоченной тройкой (или просто тройкой), если указано, какой из этих векторов является первым, какой – вторым и какой – третьим. Например, EMBED Equation.3 .

Тройка некомпланарных векторов EMBED Equation.3 называется правой (левой), если после приведения к общему началу вектор EMBED Equation.3 располагается по ту сторону от плоскости, определяемой векторами EMBED Equation.3 и EMBED Equation.3 , откуда кратчайший поворот от EMBED Equation.3 к EMBED Equation.3 кажется совершающимся против часовой стрелки (по часовой стрелке);

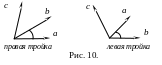
Декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку. В дальнейшем будем рассматривать только правые системы координат.

. Векторным произведением вектора EMBED Equation.3 на вектор EMBED Equation.3 называется вектор EMBED Equation.3 , обозначаемый символом EMBED Equation.3 и удовлетворяющий трем требованиям:

1) длина вектора EMBED Equation.3 равна произведению длин векторов EMBED Equation.3 и EMBED Equation.3 на синус угла EMBED Equation.3 между ними, то есть

_{EMBED Equation.3} ; (8.1)

2) вектор EMBED Equation.3 ортогонален к каждому из векторов EMBED Equation.3 и EMBED Equation.3 ;

3) вектор EMBED Equation.3 направлен так, что тройка векторов EMBED Equation.3 является правой.

Теорема. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Теорема. Длина (или модуль) векторного произведения EMBED Equation.3 равняется площади S параллелограмма, построенного на приведенных к общему началу векторах EMBED Equation.3 и EMBED Equation.3 .