6.7. Разложение вектора по базису
Три
линейно независимых вектора EMBED
Equation.3
,
EMBED Equation.3
,
EMBED Equation.3
образуют в
пространстве базис,
если любой вектор EMBED Equation.3
может быть представлен в виде некоторой
линейной комбинации векторов EMBED
Equation.3
,
EMBED Equation.3
,
EMBED Equation.3
,
т.е. для любого EMBED Equation.3
найдутся такие вещественные числа
EMBED Equation.3
,
EMBED Equation.3
,
EMBED Equation.3
,
что справедливо равенство:
EMBED Equation.3
(6.9)
– разложение вектора EMBED Equation.3 по базису EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3 , где EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3 - координаты EMBED Equation.3 относительно базиса EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3 .
Два линейно независимых вектора EMBED Equation.3 и EMBED Equation.3 образуют на плоскости базис, если любой вектор EMBED Equation.3 может быть представлен в виде некоторой линейной комбинации векторов EMBED Equation.3 и EMBED Equation.3 , т.е. для любого вектора EMBED Equation.3 найдутся такие вещественные числа EMBED Equation.3 , EMBED Equation.3 , что справедливо равенство:
EMBED Equation.3
(6.10)
Справедливы следующие утверждения:
Любая тройка некомпланарных векторов EMBED Equation.3 , EMBED Equation.3 и EMBED Equation.3 образует базис в пространстве.
Любая пара лежащих на плоскости неколлинеарных векторов EMBED Equation.3 и EMBED Equation.3 образуют базис на этой плоскости.
Каждый вектор EMBED Equation.3 может быть единственным способом разложен по базису EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3 или, координаты каждого вектора EMBED Equation.3 относительно базиса EMBED Equation.3 , EMBED Equation.3 , EMBED Equation.3 определяются однозначно.
Пример 6.5. Даны векторы
EMBED
Equation.3
Найти
разложение вектора EMBED Equation.3
по базису EMBED Equation.3
,
EMBED Equation.3
,
EMBED Equation.3
.
Решение. Запишем разложение вектора EMBED Equation.3 по базису EMBED Equation.3 , EMBED Equation.3 и EMBED Equation.3 :
EMBED Equation.DSMT4
.
Это
векторное равенство эквивалентно трем
скалярным
EMBED
Equation.3
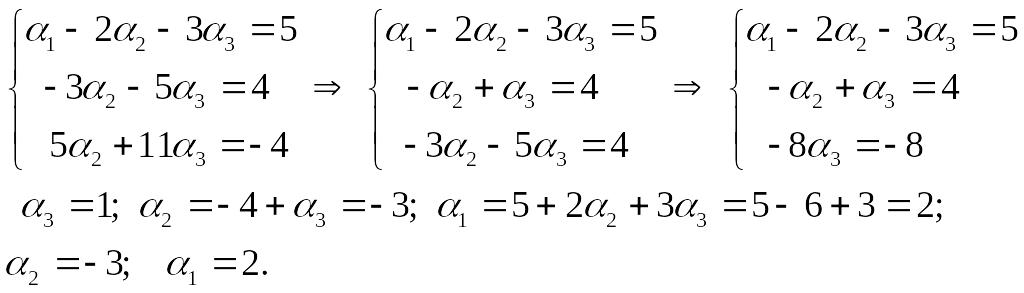Разложение
вектора EMBED Equation.3
по базису имеет вид: EMBED Equation.DSMT4
.
Вопросы для самопроверки
1. Что называется вектором и модулем вектора?
2 .Какие векторы называют коллинеарными, компланарными, равными?
3. Могут ли два вектора, имеющие равные модули, быть неравными? Если да, то чем они отличаются друг от друга?
4. Какие операции над векторами называются линейными и каковы свойства этих операций?
5. Что называется базисом на плоскости, в пространстве?
6. Как определяется декартова система координат?
7. Как выражаются координаты вектора через координаты его начальной и конечной точек?
8. Приведите формулы деления отрезка в данном отношении