
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
В.Н. Дурова М.И. Зайцева

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Учебное пособие
Воронеж 2007
ГОУВПО «Воронежский государственный
технический университет»
В.Н. Дурова М.И. Зайцева
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Воронеж 2007
УДК 517.2. (07)
Дурова В.Н. Аналитическая геометрия. Практические занятия: учеб. пособие /В.Н. Дурова, М.И. Зайцева. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2007. 153 с.
В пособии рассматриваются разделы аналитической геометрии, векторной и линейной алгебры. Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 230100 «Информатика и вычислительная техника», специальности 230104 «Системы автоматизированного проектирования».
Учебное пособие предназначено для проведения практических занятий и самостоятельной работы студентов первого курса очной формы обучения.
Учебное пособие подготовлено в электронном виде в текстовом редакторе MS WORD и содержится в файле ANALITIKA.doc.
Ил. 19. Библиогр.: 6 назв.
Научный редактор д-р физ.-мат. наук, проф. В.Д. Репников
Рецензенты: кафедра программного обеспечения и
администрирования информационных
систем Воронежского государственного
университета (зав. кафедрой д-р физ.-мат.
наук, проф. М.А. Артемов);
канд. физ.-мат. наук, доц. О.А. Соколова
© Дурова В.Н., Зайцева М.И., 2007
© Оформление. ГОУВПО
«Воронежский государственный
технический университет», 2007
Занятие 1. Вычисление определителей.
Основные свойства определителей
1.1. Понятие определителя
Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом n-го порядка этой матрицы. Начнем с определителей второго и третьего порядков.
Пусть дана матрица
А=![]() ,
,
Тогда ее определитель второго порядка вводится по формуле
det
A=![]() =
=
![]() (1.1)
(1.1)
Правило вычисления определителя второго порядка очевидно: из произведения элементов стоящих на главной диагонали вычитается произведение элементов стоящих на второй диагонали матрицы А.
В дальнейшем мы не будем приводить матрицу, для которой вычисляется определитель, так как в записи определителя содержится все элементы соответствующей матрицы.
Определитель третьего порядка вычисляется по формуле
 (1.2) Правило
вычисления определителя третьего
порядка
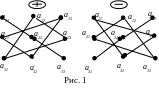
таково. Это алгебраическая сумма шести
тройных произведений элементов, стоящих
в разных строках и разных столбцах; со
знаком “плюс” берутся произведения,
сомножители которых находятся на главной
диагонали и в вершинах треугольников
с основаниями, параллельными главной
диагонали; со знаком “минус” –
произведения, сомножители которых стоят
не на главной диагонали и в вершинах
треугольников с основаниями, параллельными
этой диагонали (рис. 1).
(1.2) Правило
вычисления определителя третьего
порядка
таково. Это алгебраическая сумма шести
тройных произведений элементов, стоящих
в разных строках и разных столбцах; со
знаком “плюс” берутся произведения,
сомножители которых находятся на главной
диагонали и в вершинах треугольников
с основаниями, параллельными главной
диагонали; со знаком “минус” –
произведения, сомножители которых стоят
не на главной диагонали и в вершинах
треугольников с основаниями, параллельными
этой диагонали (рис. 1).
Порядок определителя равен порядку соответствующей матрицы.
1.2. Основные свойства определителя
1. Величина определителя не изменяется, если строки и столбцы этого определителя поменять ролями, т. е.
![]() =
=
![]() .
.
2. Перестановка двух строк (или двух столбцов) определителя равносильно уменьшению его на число (-1).
3. Если определитель имеет две одинаковые строки (или столбца), то он равен нулю.
4.
Умножение всех элементов некоторой
строки (столбца) определителя на число
![]() равносильно умножению определителя на
это число
,
т. е. общий множитель всех элементов
некоторой строки (столбца) определителя
можно выносить за знак определителя:
равносильно умножению определителя на
это число
,
т. е. общий множитель всех элементов
некоторой строки (столбца) определителя
можно выносить за знак определителя:
![]() =
=
![]() .
.
5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
6. Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.
7. Если каждый элемент n-ой строки (столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы определителей. Первый из которых имеет в n-ой строке (столбце) первые из упомянутых слагаемых и те же элементы, что и исходный определитель в остальных строках (столбцах), а второй определитель имеет в n-ой строке (столбце) вторые из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах):
![]() =
=![]() +
+![]() .
.
8. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель , то величина определителя не изменится.
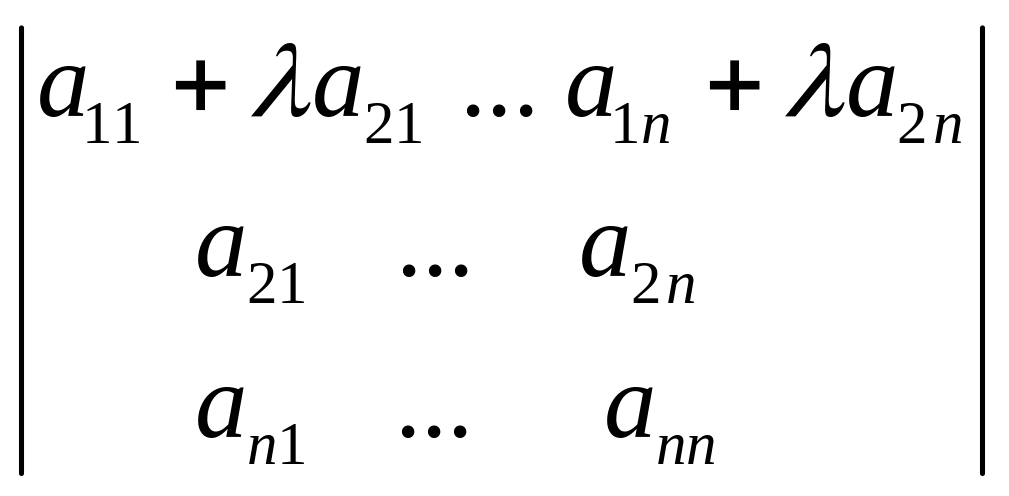 =
= +
+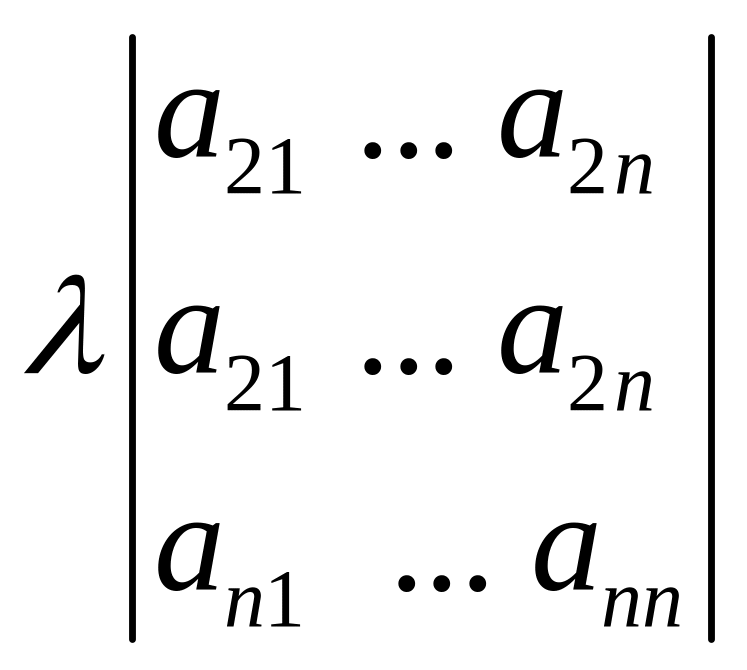 ,
,
![]() =0.
=0.
Минором
элемента
![]() определителя
n-го
порядка называется определитель (n-1)-го
порядка, получаемый из данного определителя
путем вычеркивания той строки и столбца,
на пересечении которых стоит данный
элемент. Это число
определителя
n-го
порядка называется определитель (n-1)-го
порядка, получаемый из данного определителя
путем вычеркивания той строки и столбца,
на пересечении которых стоит данный
элемент. Это число
![]() .
.
Алгебраическим дополнением любого элемента определителя называется число, равное минору этого элемента, взятому со знаком (+), если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, есть число четное и со знаком (-) – в противном случае
![]() (2.3)
(2.3)
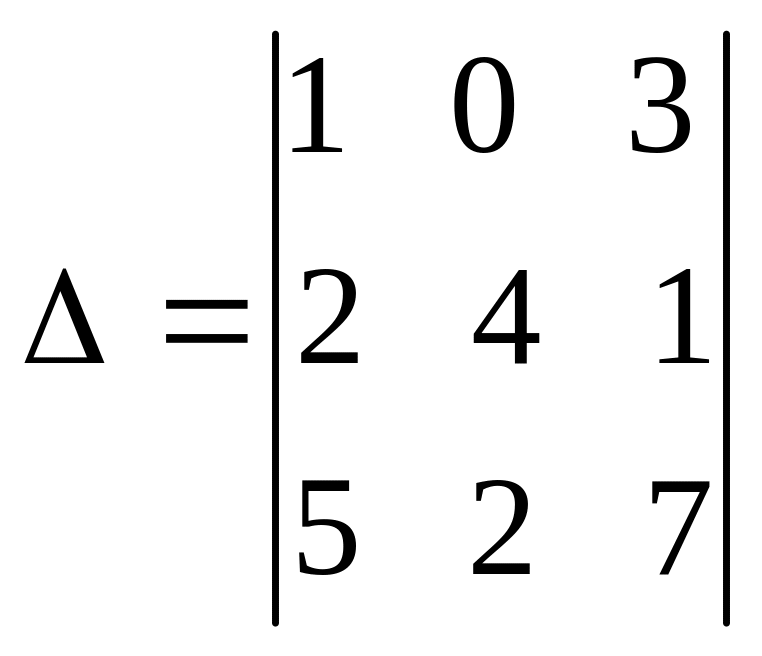 ;
;
![]() ;
;![]() .
.
9. Разложение определителя по строке (столбцу) (Один из способов вычисления определителя) Сумма произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения элементов этой строки (столбца) равна величине этого определителя.
Определитель 3-го порядка разложим по первой строке
=
![]() -
-
![]() +
+
![]() ;
;
Пример 1.1 . Вычислить определитель четвертого порядка
 .
.
Разложить определитель можно по любой строке (столбцу). Однако объем вычислений можно существенно уменьшить, если выбрать такую строку (столбец), в которой больше элементов, равных нулю. Наиболее подходящей в нашем случае является вторая строка. Разложение по ней определителя имеет вид
![]() =
=
=3(3 +14 + 48 – 126 – 2 - 8) + 2(4 + 24 + 36 - 48 - 9 - 4)= -207.
10. Сумма произведений элементов некоторой строки (столбца) определителя на соответствующее алгебраическое дополнение другой строки (столбца) равна нулю.
11.
Произведение двух определителей n-го
порядка с элементами
![]() есть в свою очередь определитель
есть в свою очередь определитель
n-го
порядка с элементами
![]() :
:
![]() .
.
12. При транспонировании матрицы определитель не меняется.
